«Ну что, без драки? Волейбол — так волейбол!»
Ну что же, USB — так USB

Не в моих правилах баловать читателя КДПВ, но не мог удержаться.
Но начнем мы, как и было обещано, со службы времени в МК. Рассмотрим связанную с этой службой задачу — имеется набор чисел и среди них следует выделить те, которые не превосходят некоторое другое наперед заданное число. А переходя к времени, можно сказать, что нам нужно будет определить момент, когда наше текущее время (Т) станет на величину интервала (И) больше, чем начало отсчета интервала (С).
Как мы можем решить эту задачу, и причем тут Уроборос?
Для начала мы должны уметь получить число Т, характеризующее текущий момент времени (неплохо бы понимать, как именно оно связано с временем, хотя это и необязательно, для начала работы достаточно знать размер числа и характер поведения этого числа при увеличении времени — нарастает оно либо уменьшается). Далее мы должны уметь запоминать текущее Т в некоторой переменной С (для чего требуется, чтобы они были однотипными — вот зачем нам знать размер). Далее мы должны уметь связывать желаемый интервал с некоторым числом И (и вот тут нам потребуются знания относительно точного поведения числа Т) и мы можем осуществить простую операцию сравнения, осуществив ее в форме
Т = С + И
— как только данное равенство выполнится, мы достигли нужного нам момента времени.
Все бы хорошо, но есть проблема проскальзывания — время течет независимо от нашего поведения, одновременно с ним изменяется переменная Т, и если мы по каким-то причинам не выполним сравнения в момент равенства, то условие будет утеряно и мы никогда не узнаем, что нужное нам время наступило (на самом деле в реальном мире узнаем, но об этом позже). Поэтому жесткое условие = следует заменить на мягкое >=, либо <=, если переменная Т уменьшается со временем и мы получаем условие Т >= С + И, которое пропустить уже намного сложнее (если вообще возможно) и все получается просто замечательно, непонятно, чем будет заполнена оставшаяся часть поста.
На самом деле подводные камни у этого решения есть, но на то они и подводные, чтобы сразу их не заметили. Рассмотрим один из них, который столько раз уже ударял по неосторожным мореплавателям, что и не сосчитаешь. И камень этот называется ограниченная разрядность или переполнение.
Проблема возникает в силу того, что время бесконечно, а разрядность чисел в МК ограничена и мы принципиально не можем натянуть несчетное множество на счетное, это аксиома. Поэтому наше число Т, какого бы размера оно не было, не может однозначно определить некоторый момент времени, а будет иметь период. Длительность этого периода будет составлять максимальное число, уменьшающееся в Т + 1, умноженное на время увеличения Т на единицу Пр = (Mах + 1) * То. К примеру, если Т увеличивается на 1 каждую микросекунду, а ширина Т составляет 32 бита, то период составит (2^32)*1е-6=4*(2^10)^3*1е-6 ~ 4 * 10^3^3 *1е-6 = 4 * 10^(9-6) = 4000 секунд, что составляет чуть больше часа. Если же Т увеличивается на 1 каждую миллисекунду, то период увеличится в тысячу раз и составит 4е6 секунд, то есть приблизительно 46 дней. Конечно, второе значение намного больше первого, но они оба меркнут по сравнению с вечностью.
И что же произойдет, когда наше число достигнет максимального значения — возможны разные варианты: оно может «лечь на упоры» и дальше оставаться неизменным (но тогда мы теряем возможность фиксировать продолжение течения времени), может начать уменьшаться (имитируя работу маятника, но тут возникают вычислительные сложности) а может принять минимальное значение, обычно это ноль (последнее явление и называется переполнением).
Как можно увеличить интервал времени, после которого данное явление произойдет — надо увеличивать любой из сомножителей, но увеличение первого повлечет за собой усложнение операций по работе с числом Т, а увеличение второго сделает невозможным работу с интервалами, менее минимального шага, что не всегда приемлемо. Поэтому выбор шага и разрядности — всегда компромисс, позволяющий и требования к МК не завысить и удобство работы не уменьшить.
Существует и другой способ расширить период — сделать связь между временем и числом Т нелинейной, лучше всего (и достаточно легко реализуемо на МК) подходит степенная функция с показателем степени менее единицы либо логарифм (кусочно-линейная его аппроксимация), но данный вариант представляет собой более теоретический интерес, нежели реальное решение, поскольку шаг приращения и, соответственно, точность увеличиваются со временем, а это для нас неприемлемо.
Так чем же нам грозит периодичность значений Т и связанное с этим переполнение (wraparound, recount, reroll, warp) — тем, что нарушается монотонность поведения Т, то есть некоторой следующий момент времени может быть представлен числом, не большим предыдущего (если у нас Т нарастает со временем), а меньшим и, соответственно, наша формула перестанет работать, причем проявления этого будут весьма неприятными — программа будет формировать интервал времени существенно меньший, нежели ожидаемый.
Вот рисунок, который следует держать в голове для понимания происходящего.
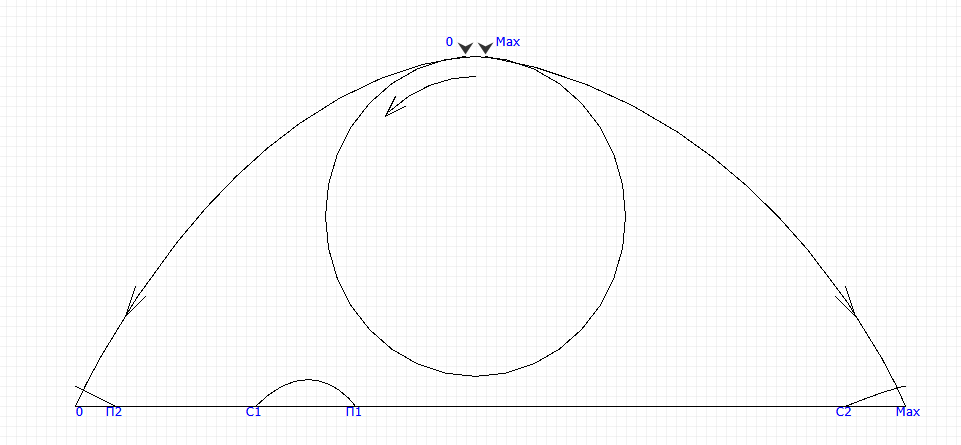
Рассмотрим пример подобного, для краткости написания будем считать, что Т размещается в байте и максимальное значение его составит 255. Если начальный момент времени для формирования интервала С = 20, а интервал И = 08, то по нашей формуле время истечет, начиная с момента 28, что правильно, а вот в случае С = 250 уже при значении Т = 251 будет выполнено условие 251 >= (250+8) = 258 — 256 = 2, что явно не соответствует нашим ожиданиям. Происходить это будет не слишком часто, вблизи конца периода и, если Вы абсолютно уверены, что Ваше устройство никогда столько времени непрерывно не проработает, то Вы можете данной особенностью пренебречь и использовать предложенную ранее формулу для отслеживания интервалов времени, что многие авторы библиотек и делают. Я категорически против подобной практики по двум причинам — во первых, надо всегда программу делать правильно, чтобы не возникало вредных привычек, а во вторых, сделать правильно совсем несложно.
Для получение правильной (верной в любом случае) формулы надо подвергнуть исходную Т >= С + И простому преобразованию и отнять от обоих частей С, получая новое условие Т — С >= И. С точки зрения математики эти условия эквивалентны, но математика работает с идеальными числами, которые имеют бесконечную ширину, хотя она совсем не беспомощна и в случае с числами ограниченными, просто надо наложить соответствующие условия. Так вот, с учетом этих условий наша новая формула правильно работает всегда. Разумеется, она верна в случае, когда Т больше С, но она работает и когда Т меньше С и происходит это в силу замечательного свойства вычитания. Представим Т в виде
Т = С + Д, где Д — добавка по отношению к старту, причем пусть даже в процессе этого прибавления мы могли получить переполнение и тогда значение Т = С + Д — Мах < С, в любом случае наша формула превращается в
(С + Д) — С = С — С + Д = Д
то есть мы получаем искомый нами интервал времени (вернее, число, его характеризующее) при любом С и Т. Почему получается именно так — это обычная уличная магия, то есть переход от абсолютной системы координат к относительной с началом в точке С.
Вычислительная сложность исходной формулы имеет одно сложение и одно сравнение, модифицированной составляет одно вычитание и одно сравнение, то есть они не отличаются (сложение, вычитание и сравнение имеют одинаковую сложность), так почему же не использовать правильную, раз это ничего не стоит. Следует отметить единственное ограничение данного метода — мы не можем заказать интервал, равный либо больше максимального представимого, то есть заказать мы можем, но получим интервал намного меньший, и это очень плохо, хотя и очевидно. И еще одно, менее очевидное ограничение — если мы закажем интервал, близкий к максимально возможному, то будет очень немного точек контроля, в которых условие выполняется, и если мы их пропустим, то пойдем на второй круг, ну и так далее. Но и в этом случае нам гарантируется, что мы получим, как минимум, то, что заказали, что намного лучше, чем ничего.
Итак, мы создали абсолютно правильный метод отсчета временных интервалов, который работает во всех возможных ситуациях (разумеется, с учетом указанных ограничений), но, как известно, совершенству нет предела. Посмотрим внимательнее на задействованные в этом методе ресурсы — нам требуется помнить две переменные и нам необходимо выполнить две операции типа сложение. Чтобы уменьшить требования по ресурсам, нужно вернуться к исходной формуле
Т >= С + И
и обратить внимание на то, что обе величины в правой части известны в момент начала формирования интервала и можно вычислить момент окончания задержки
П = С + И,
и формула превратится в выражение
Т >= П.
К сожалению, главный ее недостаток — ложное срабатывание при переполнении, остается в силе, но мы можем пойти испытанным путем и использовать вычитание Т — П >= 0.
К сожалению, обычная уличная магия нас подвела (факир был пьян и фокус не удался), поскольку данное условие выполняется всегда, так как разность любых двух чисел составляет число от 0 до Мах и всегда не меньше нуля. Вообще то, результат предсказуем, поскольку для двух произвольных чисел совершенно невозможно определить, какое из них предшествует другому, от слова «совсем» невозможно.
Попробуем создать дополнительный критерий и будем считать, что Т предшествует П в том случае, если (Т — П) < (П — Т). Неплохо для начала, но прямое вычисление по этой формуле потребует трех вычитаний — будем уменьшать. Прежде всего установим неоспоримый факт, что (Т — П) + (П — Т) = 0 = Мах + 1.
Из этого очевидного факта мы можем вывести, что Т — П будет больше, чем П — Т в том, и только том случае, если Т — П >= (Мах+1)/2. Поскольку второе выражение совершенно очевидно константное и будет вычислено на этапе компиляции, получившееся условие П — Т >= (Мах+1) /2 требует только двух операций вычитания, а память мы уже сократили на одну единицу хранения, но можно пойти и дальше.
Заметим, что для выполнения последнего условия требуется, чтобы старший бит результата был установлен, и мы могли бы воспользоваться командами условного перехода по значению бита результата, но они есть далеко не в каждом МК и транслятор может использовать их недостаточно эффективно. К счастью, именно для работы со старшим битом любой МК имеет такие команды и любой транслятор реализует их весьма хорошо — команды проверки знака числа. Дело в том, что, если рассмотреть результат, как число в дополнительном коде, то знак кодируется именно в старшем бите и проверка того, что старший бит числа содержит единицу, и того, что число является отрицательным, совпадают. Поэтому наше условие сравнения может быть записано, как Т — П < 0.
Обратим внимание на то, что мы проводим операцию вычитания с без знаковыми числами и лишь интерпретируем результат, как знаковое число при проведении операции сравнения. Данное обстоятельство должно быть учтено при написании программного кода, реализующего данный алгоритм, например для языка С соответствующий фрагмент может быть выполнен следующим образом:
if ( (long) (Т - П) < 0) ....
Итак, нам требуется помнить только одно число (П) и вычислительная сложность проверки составляет одну операцию вычитания (сравнение будет использовать ее результат и дополнительных операций не потребует), едва ли можно достигнуть лучших показателей. Чем нам пришлось заплатить за такую красоту — мы теперь не можем заказать интервал более половины максимально возможного числа, вернее, заказать можем, но он прекратится мгновенно, так что Вам решать, стоит ли выигрыш подобного ограничения. В Linux системах принят именно последний вариант, а то, что подробности скрыты за макросом — так это синтаксический сахар.
Ну, и в заключение, немного в сторону — обнаружил недавно (вообще то давно, просто подзабыл), что поведение компилятора языка С (по крайней мере некоторых из них) лично я не могу назвать логичным. Например, следующий фрагмент программы ведет себя совсем не так, как хотелось бы мне:
typedef unsigned char Timet;
Timet S = 0xF8, I = 12, T = S + I + 2;
// прости, MISRA, за предыдущую строку, я знаю, что так нельзя, но это в учебных целях
if ( (T - S) >= I) printf ( "time"); // не всегда срабатывает
register Timet D = (T - S);
if (D >= I) printf ("time"); // а вот это всегда
Мне совершенно непонятно, почему в таком виде я вижу только одно сообщение об истечении времени, а если меняю тип Timet на unsigned long, то получаю два сообщения. То есть я, конечно, лукавлю, я понимаю, почему это происходит, я не понимаю, почему было принято именно такое решение при реализации компилятора. Но, впрочем, эта проблема практически решается очень легко — включаете поддержку MISRA ( правило 10.1.b) и получаем запрет использования неудачной строки и нам придется делать все правильно, то есть надежно, нас просто заставят написать промежуточное присвоение. Причем это присвоение не стоит ничего и хороший компилятор сделает весьма эффективный код. Да, это костылик, «но ведь работает», к сожалению, другого решения просто нет.
Надо сказать, что еще более забавно выглядит следующий фрагмент кода
if ( (c = uc ) == uc) printf ( "is equal");
в процессе исполнения которого Вы не получите, весьма обоснованно, ожидаемого сообщения о равенстве при некоторых значениях переменной uc, и не получим «что самое ужасное, никакого велосипеда предупреждения». И не надо мне говорить, что эти два байта не равны — они равны и в этом то весь ужас ситуации.
Автор: GarryC





