Реализация грида для работы с большими таблицами. Часть 1

Таблица (грид) с вертикальной полосой прокрутки — наиболее распространённый элемент пользовательского интерфейса для работы с данными реляционной БД. Однако известны сложности, с которыми приходится сталкиваться, когда таблица содержит так много записей, что тактика их полной вычитки и сохранения в оперативной памяти становится неразумной.

Какие-то приложения на большие таблицы не рассчитаны и «зависают» при попытке открыть на просмотр/редактирование таблицу с миллионами записей. Иные отказываются от использования грида с вертикальной полосой прокрутки в пользу постраничного отображения или предлагают пользователю лишь иллюзию, что при помощи полосы прокрутки можно быстро перейти к нужной (хотя бы к самой последней) записи.

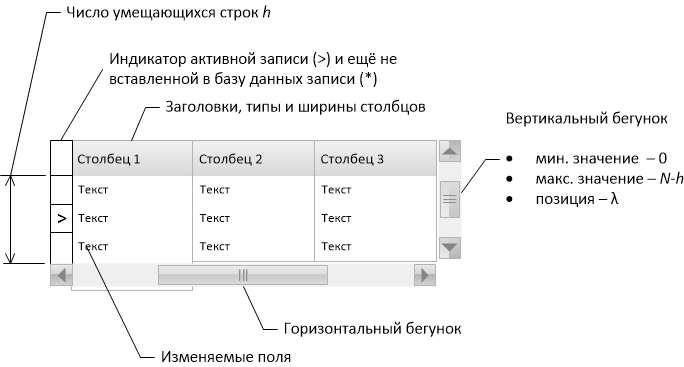
Мы расскажем об одном из возможных методов реализации табличного элемента управления, обладающего свойствами Log(N)-быстрого 1) первоначального отображения 2) прокрутки на всём диапазоне записей 3) перехода к записи с заданным уникальным ключом. Всё это — при двух ограничениях: 1) записи могут быть отсортированы только по индексированному набору полей и 2) collation-правила базы данных должны быть известны алгоритму.

Изложенные в статье принципы были реализованы автором в проекте с его участием на языке Java.

Основной принцип

Двумя ключевыми функциональными возможностями табличного элемента управления (грида) являются

1. прокрутка — отображение записей, соответствующих положению бегунка полосы прокрутки,
2. переход к записи, заданной по комбинации ключевых полей.

Сперва рассмотрим простейшие подходы к их реализации и покажем, почему они непригодны в случае большого числа записей.

Наиболее прямолинейный подход заключается в считывании в оперативную память всех записей (или хотя бы их первичных ключей), после чего прокрутка осуществляется выборкой сегмента массива, а позиционирование — поиском записи в массиве. Но при большом количестве записей, во-первых, слишком много времени занимает процесс изначальной загрузки массива и, как следствие, задерживается отображение грида на экране, а во-вторых, оперативную память начинают занимать данные таблицы, что снижает общее быстродействие.

Другой подход заключается в «перекладывании» вычислений на СУБД: выборку записей для отображения в окне прокрутки осуществлять при помощи конструкций вида select… limit… offset ... ^[1], позиционирование — сводить к select… и count(*). Однако и offset, и count(*) связаны с перебором записей внутри сервера, они имеют в общем случае скорость выполнения O(N), и потому неэффективны при большом числе записей. Частый их вызов приводит к перегрузке сервера БД.

Итак, нам нужно реализовать систему, которая не требовала бы полной закачки данных в память и при этом не перегружала бы сервер неэффективно выполняющимися запросами. Для этого поймём, какие запросы являются эффективными, а какие — нет.

При условии, что по полю k построен индекс, быстрыми являются следующие запросы (они используют index lookup и выполняются за время Log(N)):

1. Запрос A. Найти первую и последнюю запись в наборе данныx:

   select ... order by k [desc] limit 1

2. Запрос B. Найти h первых записей с ключом, большим или равным данному значению K:

   select ... order by k where k >= K limit h

Замечательным свойством запроса B является то, что в качестве параметра ему необязательно подставлять ключ существующей в базе данных записи: он одинаково быстро находит как запись по её первичному ключу, так и ближайшую к заданному ключу запись. Этим мы будем активно пользоваться.

Не являются быстрыми следующие запросы:

1. Запрос C Подсчитать общее количество записей в наборе данных:

   select count(*) ...

2. Запрос D. Подсчитать число записей, предшествующих записи с ключом, большим или равным данному:

   select count(*) ... where key < K

Запросы B и D можно обобщить на случай сортировки по набору из нескольких полей order by k1, k2, k3… при условии, что на этих полях построен составной индекс. Условие k >= K должно быть обобщено на логическое условие сравнения нескольких значений в лексикографическом порядке ^[2]:

where k1 >=  K1 and (k1 > K1 or (k2 >= K_2  and (k2 > K2 or ...)))

Основной принцип заключается в том, чтобы в процедурах, требующих быстрого отклика для пользователя, обходиться только быстрыми запросами к БД.

«Угадывание» зависимости первичного ключа от номера записи

На время представим себе, что первичный ключ нашей таблицы имеет всего одно целочисленное поле (далее мы снимем это ограничение).

Пусть каждому положению бегунка полосы прокрутки соответствует целое число от 0 до , где — общее число записей в таблице, — число строк, умещающихся на одной странице в гриде. Если бегунок полосы прокрутки выставлен в положение , то это означает, что при отрисовке грида необходимо пропустить первых записей в таблице, а затем вывести записей. Это как раз то, за что отвечают ключевые слова offset и limit в PostgreSQL, и при большом числе записей мы не можем ими пользоваться. Но если бы некоторым «волшебным» образом мы бы могли за быстрое время уметь вычислять функцию и обратную ей функцию , связывающую первичный ключ и число записей с ключом, меньшим данного, то тогда при помощи запроса B, подставляя туда значение , мы могли бы быстро получать набор записей для отображения пользователю. Задача перехода к нужной записи решалась бы таким образом: т. к. первичный ключ заранее известен, его сразу можно использовать в качестве параметра быстрого запроса B, а полосу прокрутки следовало бы установить в положение . Поставленная задача была бы решена!

(Заметим, что запрос D, вызываемый с параметром k, как раз возвращает значение , но 1) он медленный и 2) нам нужно уметь вычислять как , так и обратную ей.)

Естественно, функция целиком определяется данными в таблице, поэтому, чтобы точно восстановить взаимозависимость значений ключа и номера записи, необходимо прочесть из базы в оперативную память все ключи через одного: для корректного срабатывания запроса B в промежуточных точках можно считать, что (вспомним замечательное свойство запроса B). Это уже лучше, чем запоминать все подряд ключи, но всё ещё недостаточно хорошо, т. к. требует O(N) времени и оперативной памяти для первоначального отображения таблицы. К счастью, можно обойтись гораздо меньшим значением точно известных точек для функции , и чтобы понять это, нам потребуется небольшой комбинаторный анализ возможных значений .

Пусть мы выполнили запрос

select min(k), max(k), count(*) from foo

и получили результаты: 0, 60, 7. Т. е. теперь мы знаем, что в нашей таблице всего 7 записей (и значит, максимальное значение равно 6), первая из записей имеет ключ 0, а последняя — ключ 60. Одним таким запросом мы фактически узнали значения в трёх точках: , и . И это ещё не всё, ведь из самого определения следует, что:

1. монотонно растёт,
2. при увеличении на единицу, увеличивается на единицу или не увеличивается, поэтому график функции , кроме точки , целиком лежит в параллелограмме , , , ,
3. общее число возможных функций равно числу способов распределения ^[3] записей по значениям ключа (позиции первой и последней записи фиксированы), т. е.
   

4. число возможных функций , которые в точке принимают значение , определяется произведением количества комбинаций записей с ключом, меньшим , и большим или равным :
   

Таким образом, если каждый из возможных вариантов считать равновероятным, то вероятность того, что для заданного значения имеется ровно записей с ключом, строго меньшим , задаётся отношением , известным как гипергеометрическое распределение ^[4]. Для , картина выглядит вот таким образом:

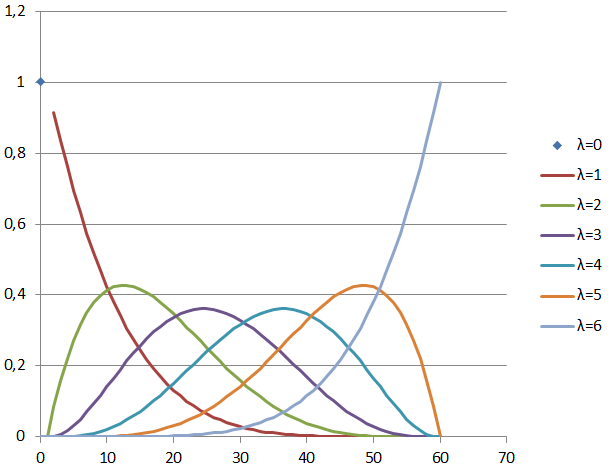
Свойства гипергеометрического распределения хорошо известны. В случае всегда , а на отрезке среднее значение линейно зависит от k:

Дисперсия значения имеет форму перевернутой параболы с нулями на краях отрезка и максимумом посередине

некрасивая формула

(Грубо можно считать, что средняя ошибка меньше, чем .)

Расчёт значений по вышеприведённым формулам для , показывает такую картину для возможных минимальных и максимальных (красные линии), среднего (голубая линия) значений , а также границ среднеквадратичного отклонения (серая область):

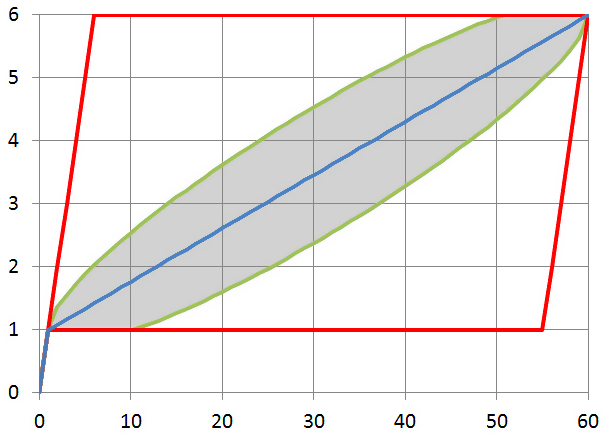
Итак, ломаная, построенная между точками , , и является статистически обоснованным приближением для вычисления функции и обратной , и это приближение даёт нам возможность довольно точно «угадать» значения функции даже если всё, что мы о ней знаем — это её значения в трёх точках, полученные при помощи одного запроса. По сути, мы для «угадывания» выполняем первую итерацию алгоритма интерполяционного поиска ^[5], только аккуратно определив граничные значения.

Если теперь для какого-то , станет известно новое точное значение , мы можем добавить пару к интерполяционной таблице и при помощи кусочной интерполяции получить уточнённый расчёт значения для решения задачи прокрутки, а применяя обратную кусочную интерполяцию, вычислять уточнённое значение при решении задачи позиционирования. С каждой накопленной точкой дипазон возможных расхождений будет сужаться, и мы будем получать всё более и более точную картину для функции .

Если ключевых полей несколько и типы данных не INT

На практике дело не ограничивается единственным целочисленным полем для сортировки набора данных. Во-первых, тип данных может быть другим: строка, дата и прочее. Во-вторых, сортируемых полей может быть несколько. Это затруднение устраняется, если мы умеем вычислять

1. функцию-нумератор , переводящую набор значений полей произвольных типов в натуральное число,
2. обратную ей функцию , переводящую натуральное число обратно в набор значений полей, .

Функция-нумератор должна обладать тем свойством, что если набор меньше набора в смысле лексикографического порядка, то должно быть .

Говоря языком математики, биекция должна устанавливать изоморфизм порядка ^[6] между множеством возможных значений наборов полей и множеством натуральных чисел. Заметим: для того, чтобы задача поиска подходящей была математически разрешима, важно, чтобы множества возможных значений полей были конечными. К примеру, между множеством всех лексикографически упорядоченных пар натуральных (пар действительных) чисел и множеством натуральных (действительных) чисел невозможно построить изоморфизм порядка. Разумеется, множество всех возможных значений любого машинного типа данных является конечным, хотя и очень большим.

Для представления значений не подходят стандартные 32- и 64-битовые целочисленные типы: так, чтобы перенумеровать одни лишь всевозможные 10-байтовые строки, уже не хватит 64-битового (8-байтового) целого. В своей реализации мы использовали класс java.math.BigInteger ^[7], способный представлять целые числа произвольной величины. При этом объём оперативной памяти, занимаемой значением , примерно равен объёму, занимаемому набором значений .

При наличии обратимой функции-нумератора и обратимой функции-интерполятора ,

• прокрутка грида сводится к вычислению значений ключевых полей , где — положение вертикальной полосы прокрутки, после чего быстрый запрос к БД находит первых записей, больших или равных ,
• позиционирование сводится к считыванию первых записей из БД по заранее известным значениям , и к вычислению положения бегунка полосы прокрутки .

Схема взаимодействия процедур

На этом этапе мы можем отвлечься от математики и разобраться собственно с алгоритмической частью. Общая схема взаимодействия процедур системы показана на рисунке ниже. Использована «приблизительная UML Activity» нотация, при этом сплошной стрелкой показана последовательность выполнения процедур, а пунктирной стрелкой — асинхронный вызов в отдельном потоке выполнения:

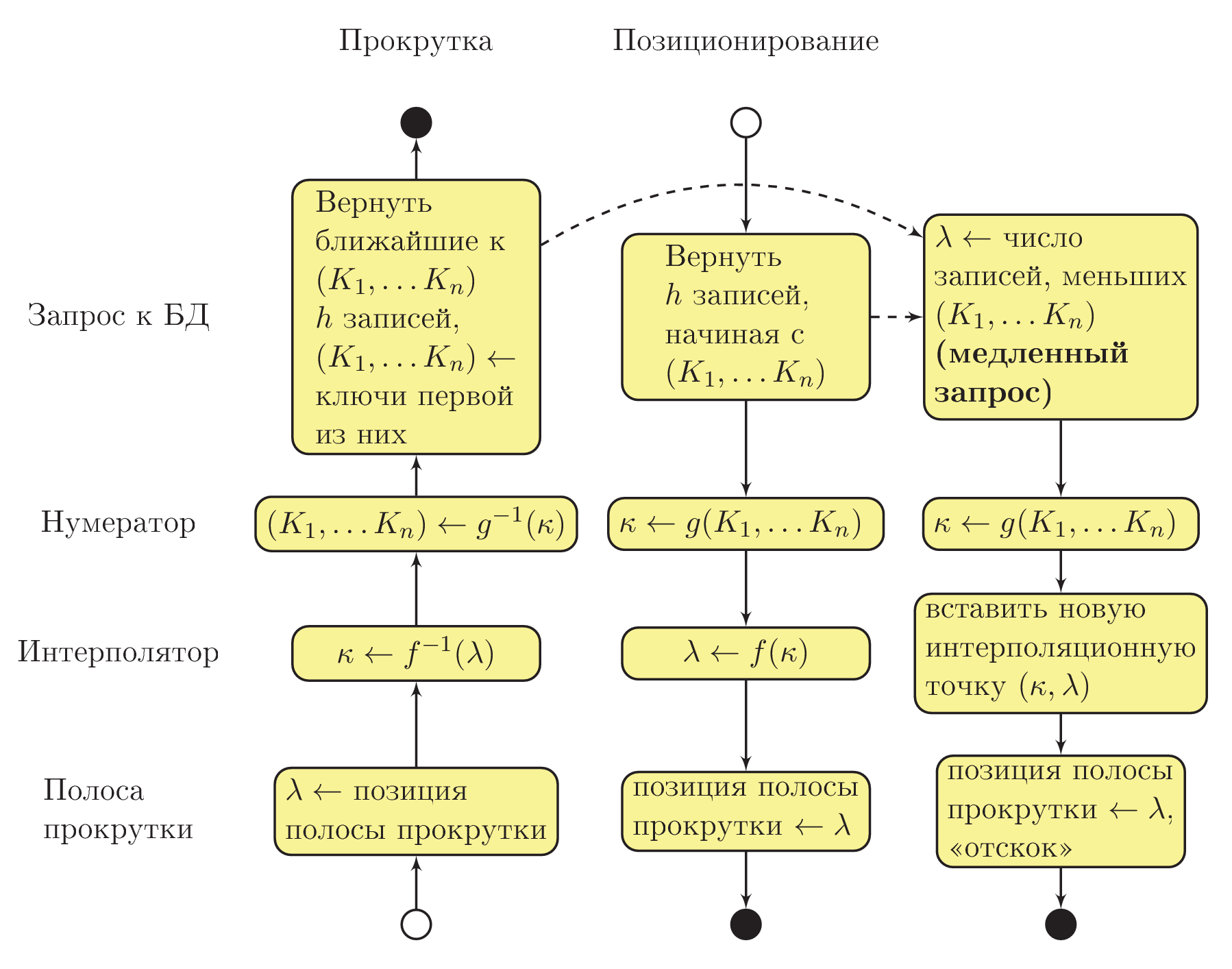
Допустим, что пользователь изменил положение бегунка вертикальной полосы прокрутки (см. в левый нижний угол диаграммы). Интерполятор вычисляет значение номера комбинации значений ключевых полей () с типом BigInteger. На основе этого значения нумератор восстанавливает комбинацию ключевых полей .

Здесь важно понимать, что на данном этапе в полях не обязательно будут находиться значения, действительно присутствующие в базе данных: там будут лишь приближения. В строковых полях, например, будет бессмысленный набор символов. Тем не менее, благодаря замечательному свойству запроса B, вывод из базы данных строк с ключами, большими или равными набору , окажется приблизительно верным результатом для данного положения полосы прокрутки.

Если пользователь отпустил полосу прокрутки и какое-то время не трогал её, асинхронно (в отдельном потоке выполнения) запускается запрос D, определяющий порядковый номер записи, а значит, и точное положение полосы прокрутки, которое соответствует тому, что отображено пользователю. Когда запрос будет завершён, на основе полученных данных будет пополнена интерполяционная таблица. Если к этому моменту пользователь не начал снова прокручивать таблицу, вертикальный бегунок «отскочит» на новое, уточнённое положение.

При переходе к записи последовательность вызовов процедур происходит в обратную сторону. Т. к. значения ключевых полей уже известны, для пользователя запросом B сразу извлекаются данные из базы. Нумератор вычисляет , и затем интерполятор определяет приблизительное положение полосы прокрутки как . Параллельно, в асинхронном потоке выполнения, выполняется уточняющий запрос, по результатам которого в интерполяционную таблицу добавляется новая точка. Через секунду-другую бегунок полосы прокрутки «отскочит» на новое, уточнённое положение.

Чем больше пользователь будет «бродить» по данным вертикальным бегунком, тем больше точек будет собираться в интерполяционной таблице и тем меньше будут «отскоки». Практика показывает, что достаточно всего 4-5 удачных точек в интерполяционной таблице, чтобы «отскоки» стали очень малы.

Экземпляр класса-интерполятора должен хранить в себе промежуточные точки монотонно растущей функции между множеством 32-битных целых чисел (номеров записей в таблице) и множеством объектов типа BigInteger (порядковых номеров комбинаций значений ключевых полей).

Сразу же после инициализации грида необходимо в отдельном потоке выполнения запросить общее количество записей в таблице, чтобы получить корректное значение . До того момента, как это значение будет получено при помощи выполняющегося в параллельном потоке запроса, можно использовать некоторое значение по умолчанию (например, 1000) — это не повлияет на корректность работы.

Интерполятор должен уметь за быстрое по количеству интерполяционных точек время вычислять значение как в одну, так и в другую сторону. Однако заметим, что чаще требуется вычислять значение порядкового номера комбинации по номеру записи: такие вычисления производятся много раз за секунду в процессе прокрутки грида пользователем. Поэтому за основу реализации модуля интерполятора удобно взять словарь на основе бинарного дерева, ключами которого являются номера записей, а значениями — порядковые номера комбинаций (класс TreeMap<Integer, BigInteger> в языке Java).

Ясно, что по заданному номеру такой словарь за логарифмическое время находит две точки (), между которыми строит прямую интерполяцию функции . Но тот факт, что растёт монотонно, позволяет за быстрое время производить и обратное вычисление. В самом деле: если дан номер комбинации , , поиск кусочного сегмента, в котором лежит , можно произвести в словаре методом дихотомии. Отыскав нужный сегмент, мы производим обратную интерполяцию и находим номер , соответствующий .

При пополнении словаря интерполяционными точками необходимо следить за тем, чтобы интерполируемая функция оставалась монотонной. Так как другие пользователи могут удалять и добавлять записи в просматриваемую таблицу, актуальность известных словарю интерполяционных точек может утратиться, а вновь добавляемая точка может нарушить монотонность. Поэтому метод добавления новой интерполяционной точки должен проверять, что «точке слева» от только что добавленной соответствует меньшее, а «точке справа» — большее значение. Если оказывается, что это не так, следует исходить из предположения, что последняя добавленная точка соответствует актуальному положению вещей, а некоторые из старых точек утратили свою актуальность. По отношению к вновь добавленной точке следует удалять все точки слева, содержащие большее значение, и все точки справа, содержащие меньшее значение. Процесс «срезания выбивающейся точки» показан на рисунке:

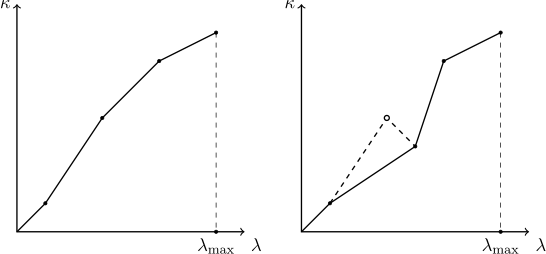
Также интерполятор должен содержать в себе механизм, в целях экономии памяти защищающий словарь от переполнения излишними точками, и отбрасывающий наименее существенные из них (как мы помним, не имеет смысла хранить все точки подряд — достаточно только через одну).

Заключение к первой части

Итак, мы разобрались, как в целом устроена наша система: основными её частями являются интерполятор и нумератор, а также полностью обсудили реализацию интерполятора. Чтобы завершить решение задачи, необходимо теперь реализовать нумератор — биекцию , увязывающую наборы значений ключевых полей, возможно, состоящих из дат, строки, отсортированных при помощи Unicode collation rules и т. п. с растущими в том же порядке числами.

Этому будет посвящена вторая часть статьи.

Ещё я готовлю научную публикацию, и вы можете также ознакомиться с препринтом научной версии этой статьи на arxiv.org ^[8].

Автор: IvanPonomarev

Источник ^[9]