Генетическое программирование. ELTRUT-проблема

Бродя по просторам интернета, заинтересовался такой вещью как генетическое программирование. Если в двух словах, это автоматическое создание программ, которые выполняют ту или иную цель, в соответствии с принципом естественного отбора. То есть сначала случайным образом создается поколение «существ»-программ, которые сортируются по разным критериям (близость к достижению цели), затем часть из них мутирует (также случайно), часть вымирает и часть заменяется новыми случайными существами.

Таким образом, самые достойные существа продолжают свое дело и дают потомков, а самые слабые — отсеиваются в процессе отбора. Несколько экспериментов и их результаты — под катом.

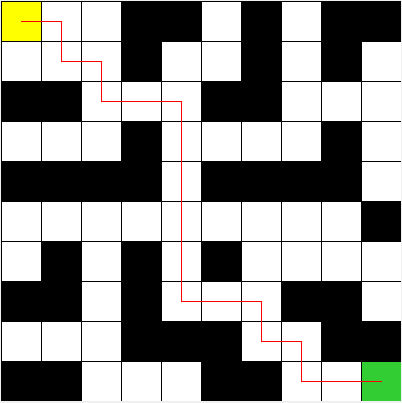
Первые пробы. Прохождение по лабиринту

В качестве пробы пера я решил научить существ (будем называть их так, поскольку термин «программа» слишком громкий для этого случая) искать путь в лабиринте, как на картинке сверху. Сразу оговорюсь, что в данном случае целью было не вывести с помощью генной инженерии существо, которое будет находить путь в произвольном лабиринте, а найти путь в одном конкретном лабиринте, причем чтобы у существ не было органов чувств. После недолгих размышлений было решено использовать простой набор команд, который может легко мутировать и исполняться существом. Итак, наша «программа», или «геном» — это просто набор команд, в какую сторону следует продвинуться существу. В дополнение, был добавлен цикл, который сможет повторять участок программы несколько раз. Геном может быть, например таким:

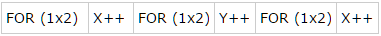
Здесь команда FOR (IxT) означает, что следующие I инструкций будут выполнены T раз. Существо с таким геномом пройдет на 2 клетки вправо, затем на 2 клетки вниз и еще раз на 2 клетки вправо.

Теперь займемся нашим существом, по сути являющимся интерпретатором генома. У каждого нашего существа будет «имя», или идентификатор, по которому мы потом будем его узнавать, «геном», по которому наше существо будет действовать, метод Step, по которому существо будет выполнять следующий ген (при этом будем проверять, не ходит ли существо сквозь стены), функция Fitness, которая будет определять, насколько близко существо подобралось к финишной клетке, и метод Mutate, который будет менять часть генома. О мутациях чуть позже, а пока посмотрим, как наш милый квадратик выполняет нашу тестовую программу:

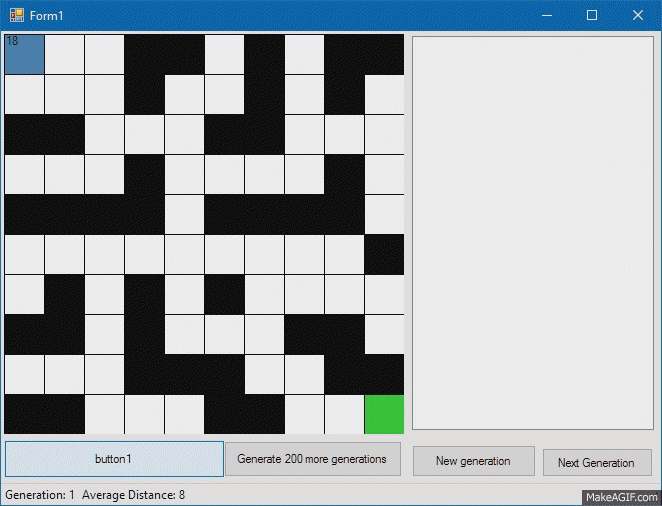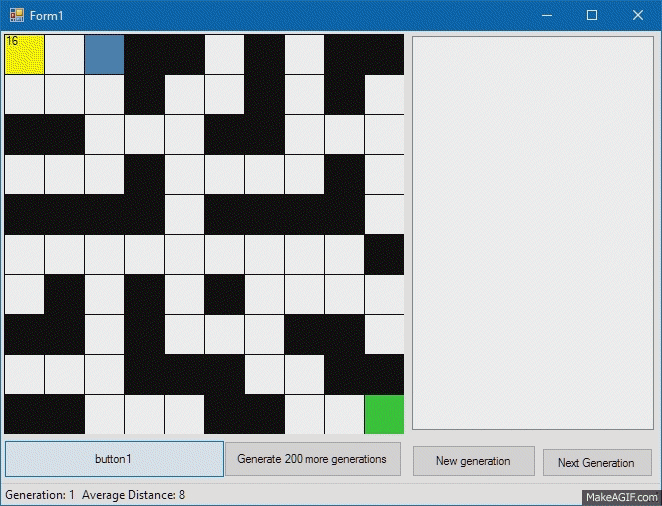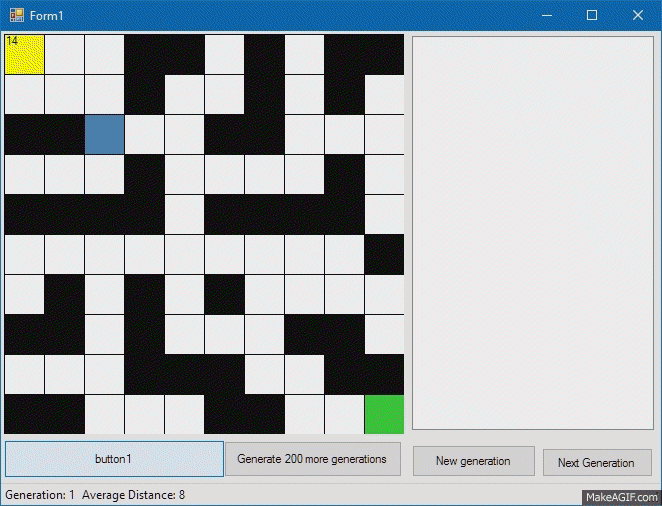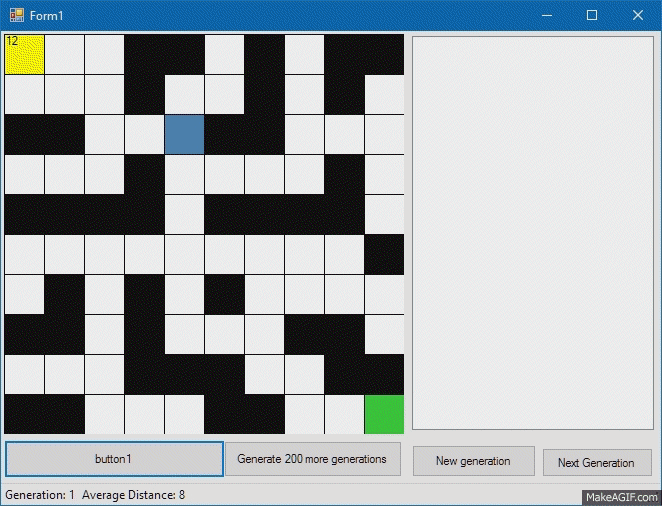
Fitness, или соответствие существа нашим требованиям будем считать как сумму разностей координат финиша и существа. Так, существо с наименьшим расстоянием до цели будет наиболее подходящим.

Эволюция

Существа у нас будут эволюционировать поколение за поколением, по 100 существ в каждом. В рамках каждого поколения мы будем повторять одни и те же шаги:

• Проверка существ на соответствие (вычисление Fitness);
• Сортировка существ по возрастанию расстояния до цели;
• В зависимости от положения в списке:
  — либо не будем менять существо, с предположением что оно и так достаточно хорошо, и незачем его портить;
  — либо изменяем геном: удаляем, добавляем, изменяем часть генов;
  — либо заменяем новым случайным существом, старое при этом «вымирает» как недостойное к продолжению рода.

Методом тыка выберем такое отношение: 10 лучших не меняем, следующие 60 мутируют, остальные 30 вымирают. Пробуем, на 292 поколении получаем результат:

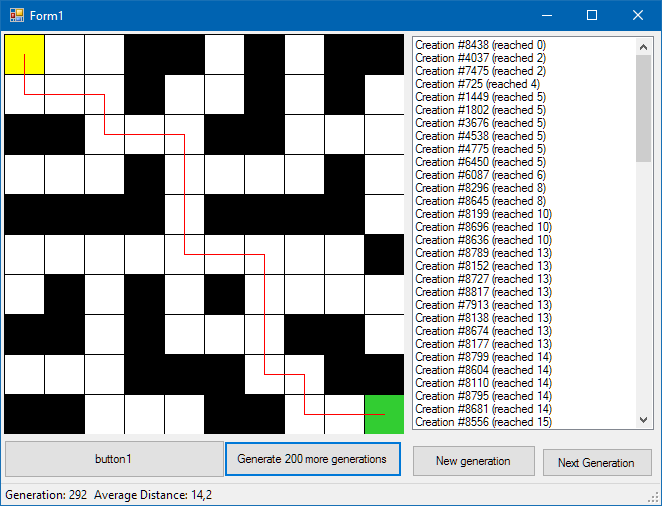
Геном нашего победителя такой:

Y_INC; X_INC; Y_INC; FOR_2x3; X_INC; Y_INC; FOR_1x4; X_DEC; FOR_2x3; Y_INC; X_INC; Y_DEC; Y_INC; FOR_2x4; Y_INC; X_INC; Y_INC; FOR_2x4; X_DEC; X_INC; X_INC;

Как можно увидеть, существо часто топчется на одном месте, что, в общем-то, не совсем хорошо. Попробуем взять в расчет еще и длину генома. Но поставим ее на второе место по важности после расстояния до финиша, чтобы не оказалось так, что короткие программы из 2-3 генов, которые стоят на старте, оказались лучше в сравнении с теми, которые доходят ближе до цели, но при этом имеют длинный геном. Методом, опять же, тыка, пробуем формулу:

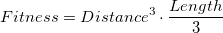
Теперь поиск решения идет несколько дольше. На 335 поколении мы получаем точно такой же результат, но уже со следующим геномом:

FOR_2x4; X_INC; Y_INC; FOR_2x3; Y_INC; X_INC; Y_DEC; Y_INC; FOR_2x4; Y_INC; X_INC;

Собственно, здесь еще многое можно доработать, но задача решена, с приемлемым качеством и с приемлемыми трудозатратами. Свой код я намеренно не привожу в связи с его недоработанностью. Поэтому с чистой совестью можно перейти к теме, вынесенной в заголовок.

ELTRUT-проблема

В 2012 году выпускник Университета штата Калифорния Бенджамин Буш занимался генетическими алгоритмами и, в частности, так называемой ELTRUT-проблемой. Суть задачи такова: существует растровое изображение, найти последовательность команд для черепашки Лого, которая нарисует подобное изображение. Вот видео, где все довольно доступно объяснено:

Если коротко, Бенджамин предлагает такое решение: откажемся от простого линейного генома в пользу двумерного. Почему? Потому что двумерный геном обладает избыточностью, так что далеко не каждая мутация спровоцирует кардинальное изменение генома. Также Бенджамин предлагает интересную форму представления генома: каждому пикселу изображения сопоставляется ген, который указывает в какую сторону и на какое расстояние отправиться черепашке, если она попадет в эту точку, и нужно ли ей при этом рисовать линию. Визуально геном можно отобразить так:

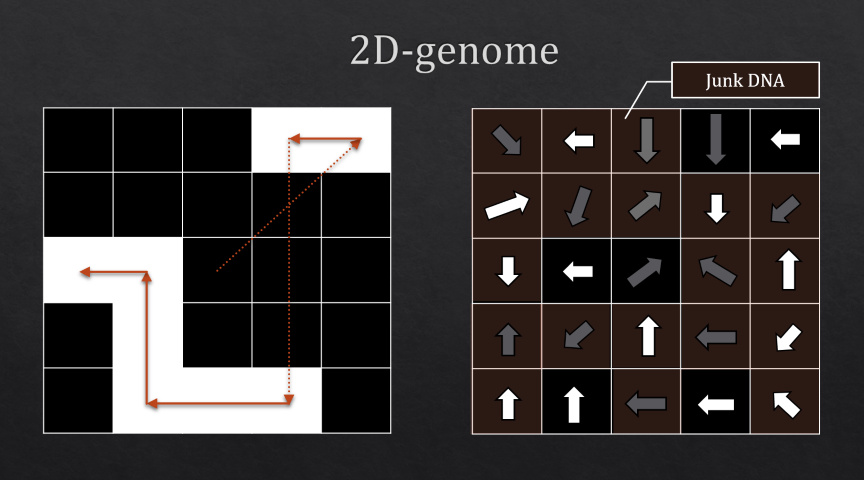
Здесь коричневым выделен избыточный геном. Видно, что почти в 80% мутаций изменений в поведении черепашки не произойдет. Вдобавок, при решении этой задачи предлагается использовать «половое размножение», или кроссинговер: два существа предыдущего поколения обмениваются генами, чтобы получить потомков. Далее идет речь о трехмерном геноме и об оптимизации алгоритма, но оптимизацией я заниматься не хотел, да и три измерения это несколько чересчур для ознакомления с генетическими алгоритмами, поэтому я решил остановиться на воплощении упрощенного алгоритма.

Итак, аналогично предыдущей задаче, в каждом поколении у нас будет по 100 существ. В каждом поколении мы будем:

• Скрещивать 50 лучших существ и заменять 50 худших их потомками;
• Изменять по одному гену каждому существа, кроме 10 лучших;
• Если существо уже выполнило свою задачу, то оно мутировать не будет.

Как мы будем определять степень соответствия существ? За каждый правильно нарисованный пиксел начислим существу некоторое количество очков, за каждый неверно нарисованный будем штрафовать. Если там, где пиксел не закрашен, и он не должен быть закрашен, не меняем счет. Итого, примерный алгоритм подсчета очков:

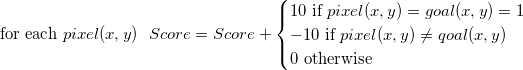
Сразу решим еще одну проблему (как раз она и должна решаться трехмерным геномом): если черепашка встанет на пиксел, где она уже была, то выполнение программы зациклится. Поэтому сделаем так, чтобы наступив на посещенный пиксел, черепашка останавливалась. Заодно мы не будем до посинения гонять бедную рептилию.

Итак, пробуем. Изображение 5х5, не очень сложное, сможем ли мы получить результат?

Неплохо, но как программа справится с несколько большим изображением, например, 8х8?

Видео сильно ускорено (предыдущее тоже ускорено, но слегка). 2000 поколений так и не дали правильный результат. Можно было бы попробовать продолжить, но как видно по графику, около 1000 поколений никаких изменений не происходило, так что вряд ли это решило проблему. Ну и нелюбовь к оптимизации сделали свое дело: на изображение 8х8 потребовалось около 2 часов на моем компьютере. Так что, эксперимент признается частично проваленным.

Спасибо за уделенное время, надеюсь, эта статья покажется кому-то интересной.

Автор: JGDger

Источник