Здравствуй!
В статье, опубликованной на Хабре в прошлом году, мы решали задачу определения математически обоснованных стоимостей шахматных фигур. С помощью регрессионного анализа партий, сыгранных компьютерами и людьми, нам удалось получить шкалу ценности «юнитов», во многом совпадающую с традиционными значениями, известными из книг и практического опыта.
К сожалению, непосредственная подстановка скорректированных значений для фигур не усилила программу автора — во всяком случае, больше, чем в рамках статистической погрешности. Применение же исходного метода «в лоб» к другим параметрам оценочной функции давало несколько абсурдные результаты, алгоритм оптимизации явно нуждался в некоторой доработке. Тем временем, автор решил, что очередной релиз его движка станет заключительным в длинной серии версий, берущих своё начало в коде десятилетней давности. Была выпущена версия GreKo 2015, и дальнейшие изменения в ближайшем будущем не планировались.
Всем интересующихся тем, что было дальше — после просмотра картинки для привлечения внимания добро пожаловать под кат.
Мотивацией к внезапному продолжению работы и, в конечном итоге, появлению этой статьи, послужили два события. Одно из них прогремело на весь мир по каналам массовой информации — это матч в Го корейского топ-игрока Ли Седоля с программой Google AlphaGo.
Разработчики из Google DeepMind сумели эффективно объединить две мощные техники — поиск в дереве методом Монте-Карло и глубокое обучение с использованием нейросетей. Получившийся симбиоз привёл к феноменальным результатам в виде победы над двумя профессиональными игроками в Го (Ли Седолем и Фан Хуэем) с общим счётом 9 — 1. Детали реализации AlphaGo широко обсуждались, в том числе и на Хабре, поэтому сейчас останавливаться на них не будем.
Второе событие, не столь широко разрекламированное, и замеченное в основном энтузиастами шахматного программирования — появление программы Giraffe. Её автор, Matthew Lai, активно использовал идеи машинного обучения, в частности, всё те же глубокие нейросети. В отличие от традиционных движков, в которых оценочная функция содержит ряд заранее предопределённых признаков позиции, Giraffe на этапе обучения самостоятельно извлекает эти признаки из учебного материала. Фактически, была заявлена цель автоматического вывода «шахматного знания» в том виде, в котором его излагают в учебниках.
Кроме оценочной функции, нейронные сети в Giraffe использовались и для параметризации поиска по дереву, что также наводит на мысли о некоторых параллелях с AlphaGo.
Определённые успехи программа продемонстрировала, достигнув с нуля за несколько дней обучения силы международного мастера. Но, к сожалению, интереснейший исследовательский проект был преждевременно завершён… в связи с переходом Matthew Lai на работу в команду Google DeepMind!
Так или иначе, информационная волна, возникшая в связи с AlphaGo и Giraffe, побудила автора данной статьи ещё раз вернуться к коду своего движка и попытаться всё-таки усилить его игру методами столь популярного ныне машинного обучения.
Алгоритм
Возможно, кого-то это разочарует, но в описываемом проекте не будет ни многослойных нейронных сетей, ни автоматического детектирования ключевых признаков позиции, ни метода Монте-Карло. Случайный поиск по дереву в шахматах практически не требуется в силу ограниченности задачи, а хорошо работающие факторы оценки шахматной позиции известны ещё со времён «Каиссы». Кроме того, автору было интересно насколько можно усилить игру программы в рамках достаточно минималистичного их набора, который реализован в GreKo.
Базовым методом был выбран алгоритм настройки оценочной функции, который предложил шведский исследователь и разработчик Peter Österlund, автор сильной программы Texel. Выигрышными сторонами этого метода, по словам его создателя, являются:
- Возможность одновременно оптимизировать до нескольких сотен параметров оценочной функции.
- Отсутствие необходимости в источнике «внешнего знания» в виде экспертных оценок позиций — нужны только тексты и результаты партий.
- Корректная работа с сильно коррелированными признаками — не требуется никакая предварительная подготовка вроде их ортогонализации.
Пусть θ = (θ1, ..., θK) — вектор параметров оценочной функции (веса материала и позиционных признаков).
Для каждой позиции pi, i = 1...N из тестового набора мы вычисляем её статическую оценку Eθ(pi), представляющую собой некоторую скалярную величину. Традиционно оценку нормируют так, чтобы она давала представление о перевесе той или другой стороны в единицах шахматного материала — например, сотых долях пешки. Мы будем рассматривать оценку всегда с точки зрения белых.
Перейдём теперь из материального представления оценки в вероятностное. С помощью логистической функции сделаем следующее преобразование:
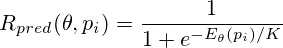
Величина Rpred имеет смысл математического ожидания результата партии для белых в данной позиции (0 — поражение, 0.5 — ничья, 1 — победа). Нормировочная константа K может быть определена как такой материальный перевес, при котором «всё становится ясно». В данном исследовании использовалось значение K = 150, т.е. полторы пешки. Разумеется, «становится ясно» только в статистическом смысле, в реальных шахматных партиях можно найти огромное количество контрпримеров, когда к выигрышу не приводит и гораздо больший материальный перевес.
В оригинальном алгоритме вместо статической оценочной функции для вычисления Rpred использовался результат так называемого ФВ-поиска. Название связано с понятием форсированного варианта, в английском варианте — quiescence search. Это альфа-бета поиск из заданной позиции, в котором рассматриваются только взятия, превращения пешек, иногда — шахи и уходы от них. Хотя деревья перебора получаются небольшими, по сравнению со статической оценкой скорость вычисления уменьшается в десятки и сотни раз. Поэтому было решено использовать более быструю схему, а динамичные позиции отсеивать на этапе подготовки исходных данных.
Теперь, зная для каждой позиции предсказанный Rpred и фактический Rfact результаты партии, в которой она встретилась, мы можем вычислить среднеквадратичную ошибку предсказания:
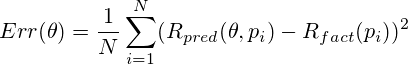
Фактически, полученная среднеквадратичная оценка уже может рассматриваться как целевой функционал, подлежащий минимизации. Такой подход изложен в оригинальном описании метода.
Сделаем ещё одну небольшую модификацию — введём учёт оставшегося до конца партии количества ходов. Очевидно, что позиционный признак, существовавший на доске в самом начале партии, может вообще никак не влиять на её исход, если основные события в игре произошли гораздо позже. Например, белые в дебюте могут иметь гордого коня в центре доски, но проиграть в глубоком эндшпиле, когда этот конь уже давно разменян, из-за вторжения неприятельской ладьи в свой лагерь. В данном случае признак «конь в центре доски» не должен получать слишком большого наказания по сравнению с признаком «ладья на второй горизонтали» — конь-то ни в чём не виноват!
Соответственно, добавим в нашу целевую функцию поправку, связанную с числом оставшихся до конца партии ходов ni. Для каждой позиции она будет представлять собой множитель экспоненциального затухания с параметром λ. «Физический смысл» этого параметра — количество ходов, в течение которого тот или иной позиционный признак оказывает влияние на партию. Опять же, в среднем. В описанных ниже экспериментах λ принимает значения в несколько десятков полуходов.
В оригинальном описании Texel's Tuning Method из обучающей выборки отбрасывались первые ходы в партиях. Введение "λ-забывания" позволяет нам не вводить явное ограничение на ходы из дебютной книги — их влияние так или иначе оказывается малым.
Окончательный вид нашего целевого функционала:
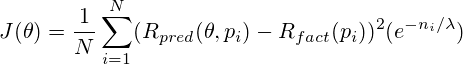
Задача обучения оценочной функции сводится теперь к минимизации J в пространстве значений вектора θ.
Почему этот метод работает? Фактически, бо́льшая часть признаков, возникающих в позициях на больших массивах партий, из-за усреднения взаимно нейтрализуются. Сохраняют своё значение и получают более высокие веса только те из них, которые реально оказали влияние на результат. Чем раньше оценочная функция в ходе партии начнёт их замечать — тем лучше будет предсказание и точнее оценка позиции, тем более сильную игру станет демонстрировать программа.
Обучение и результаты
В качестве массива данных для обучения использовались позиции из 20 тысяч партий, сыгранных программой с самой собой. Из их числа были исключены позиции, возникшие после взятия фигуры или объявления шаха. Это необходимо для того, чтобы обучающее множество примеров как можно лучше совпадало с реальными позициями из дерева перебора, для которых применяется статическая оценка.
В результате получилось порядка 2.27 млн. позиций. Не все они уникальные, но для используемого метода это не является критичным. Позиции случайным образом были разделены на тренировочный и проверочный наборы в соотношении 80 / 20, соответственно 1.81 млн. и 460 тыс. позиций.
Минимизация функционала проводилась на тренировочном наборе методом покоординатного спуска. Известно, что для задач многомерной оптимизации этот метод обычно не является наилучшим выбором. Однако, в пользу данного алгоритма сыграли простота реализации, а также приемлемое время выполнения. На типичном современном PC оптимизация для 20 тыс. партий занимает от одного до нескольких часов, в зависимости от выбранного для настройки подмножества из 27 возможных весов.
Ниже приведён график изменения функционала в зависимости от времени. Критерием остановки обучения является неулучшение результата для проверочного подмножества после очередного цикла спусков по всем параметрам.
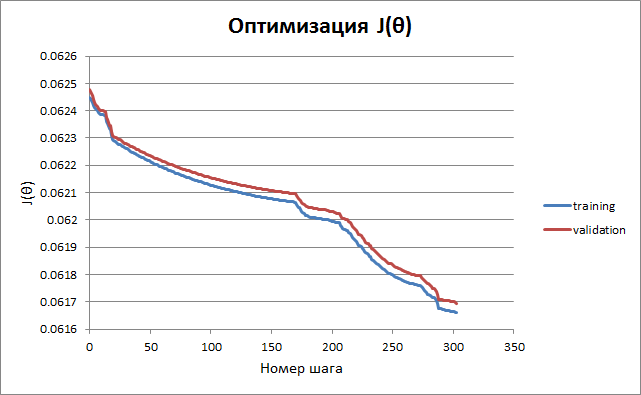
Эволюция группы параметров, имеющих отношение к пешкам, показана на следующем графике. Видно, что процесс сходится достаточно быстро — по крайней мере, к локальному минимуму. Задача поиска глобального минимума пока не ставилась, наша цель сейчас — усилить программу хотя бы на какую-то величину…
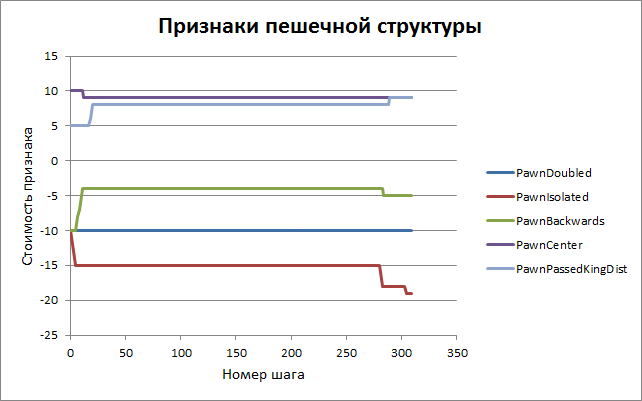
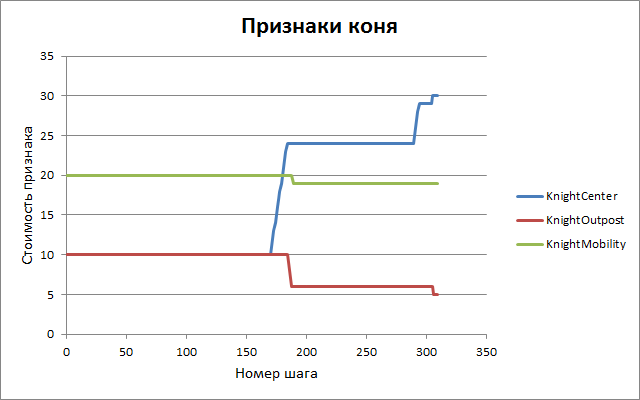
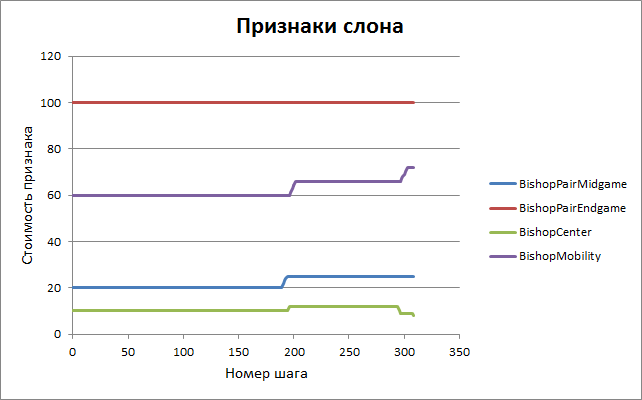
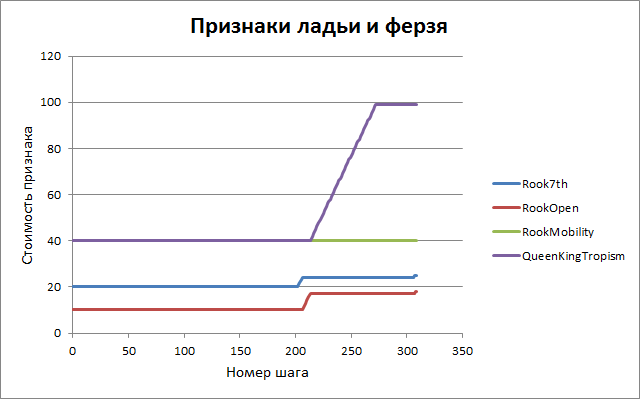
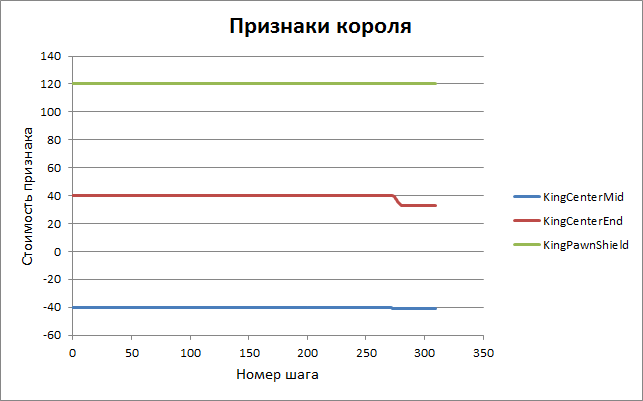
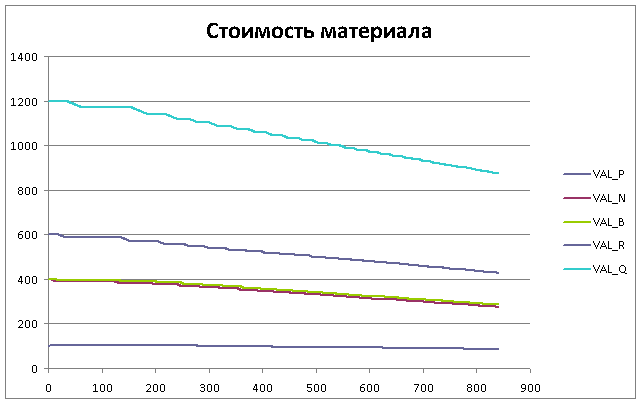
Приведём полный список параметров оценки с начальными и конечными значениями. Смысл большей части понятен без дополнительных комментариев, желающие ознакомиться с точным их назначением приглашаются в исходный код программы — файл eval.cpp, функция Evaluate().
| Номер | Признак | Описание | До обучения | После обучения |
|---|---|---|---|---|
| 1. | VAL_P | стоимость пешки | 100 | 100 |
| 2. | VAL_N | стоимость коня | 400 | 400 |
| 3. | VAL_B | стоимость слона | 400 | 400 |
| 4. | VAL_R | стоимость ладьи | 600 | 600 |
| 5. | VAL_Q | стоимость ферзя | 1200 | 1200 |
| 6. | PawnDoubled | сдвоенная пешка | -10 | -10 |
| 7. | PawnIsolated | изолированная пешка | -10 | -19 |
| 8. | PawnBackwards | отсталая пешка | -10 | -5 |
| 9. | PawnCenter | пешка в центре доски | 10 | 9 |
| 10. | PawnPassedFreeMax | незаблокированная проходная | 120 | 128 |
| 11. | PawnPassedBlockedMax | заблокированная проходная | 100 | 101 |
| 12. | PawnPassedKingDist | удалённость проходной от короля противника в эндшпиле | 5 | 9 |
| 13. | PawnPassedSquare | проходная, недостижимая по «правилу квадрата» | 50 | 200 |
| 14. | KnightCenter | централизация коня | 10 | 27 |
| 15. | KnightOutpost | защищённый пункт для коня | 10 | 7 |
| 16. | KnightMobility | мобильность коня | 20 | 19 |
| 17. | BishopPairMidgame | пара слонов в миттельшпиле | 20 | 20 |
| 18. | BishopPairEndgame | пара слонов в эндшпиле | 100 | 95 |
| 19. | BishopCenter | централизация слона | 10 | 9 |
| 20. | BishopMobility | мобильность слона | 60 | 72 |
| 21. | Rook7th | ладья на 7-й горизонтали | 20 | 24 |
| 22. | RookOpen | ладья на открытой вертикали | 10 | 17 |
| 23. | RookMobility | мобильность ладьи | 40 | 40 |
| 24. | QueenKingTropism | близость ферзя к королю противника | 40 | 99 |
| 25. | KingCenterMid | централизация короля в миттельшпиле | -40 | -41 |
| 26. | KingCenterEnd | централизация короля в эндшпиле | 40 | 33 |
| 27. | KingPawnShield | пешечный щит короля | 120 | 120 |
В таблице приведён пример для одной из сессий обучения, в которой оптимизировались только позиционные параметры оценки, а стоимости фигур оставались неизменными. Это не является критическим требованием, в ходе описанных ниже тестов использовалось и полное обучение по всем 27 параметрам. Но наилучшие результаты в практической игре показала версия с неизменной шкалой материала.
Какие можно сделать выводы из полученных весов? Видно, что некоторые из них остались практически неизменными по сравнению с оригинальной версией программы. Можно предположить, что за годы отладки движка они были подобраны интуитивно достаточно верно. Однако, в некоторых моментах холодная математика внесла поправки в человеческую интуицию. Так, вред отсталых пешек был автором переоценен. А вот следующие параметры показались алгоритму более важными, их веса были подняты практически вдвое:
- изолированная пешка
- ладья на открытой вертикали
- удалённость проходной от короля противника в эндшпиле
- централизация коня
- близость ферзя к королю противника
Отдельно стоит упомянуть признак проходной, недостижимой по «правилу квадрата». Его оптимизированное значение достигло поставленной в алгоритме границы допустимого интервала. Очевидно, оно могло бы оказаться и больше. Причина, вероятно, в том, что в обучающем файле при наличии такой проходной пешки партии выигрывались в 100% случаев. В качестве веса было оставлено значение 200, как вполне достаточное — на силу игры его увеличение практически не влияет.
Проверка за шахматной доской
Итак, мы обучили оценочную функцию предсказывать исход партии на основании позиции на доске. Но впереди главная проверка — насколько это умение окажется полезным в практической игре. С этой целью было подготовлено несколько версий движка с различными настройками, каждая из которых получена в своём режиме обучения.
| Версия | Обучающий файл | Число партий | Коэффициенты оценки | Константа масштабирования λ |
|---|---|---|---|---|
| A | 20000.pgn | 20000 | 6...27 | 40 |
| B | 20000.pgn | 20000 | 1...27 | 40 |
| C | 20000.pgn | 20000 | 6...27 | 20 |
| D | 20000.pgn | 20000 | 1...27 | 20 |
| E | 20000.pgn | 20000 | 6...27 | 60 |
| F | 20000.pgn | 20000 | 1...27 | 60 |
| G | gm2600.pgn | 27202 | 6...27 | 20 |
| H1 | large.pgn | 47202 | 6...27 | 20 |
| H2 | large.pgn | 47202 | 1...27 | 20 |
20000.pgn — партии программы с самой собой (суперблиц)
gm2600.pgn — партии гроссмейстеров с FTP-сайта автора Crafty Роберта Хьятта (классический контроль)
large.pgn — объединение двух этих файлов
Каждая из версий сыграла по 100 партий с исходной программой GreKo 2015, а также с набором других движков с контролем времени «1 секунда + 0.1 секунды на ход». Результаты приведены в таблице ниже. С помощью программы bayeselo были подсчитаны относительные рейтинги версий, сила GreKo 2015 зафиксирована в качестве точки отсчёта на уровне 2600. Определена также величина LOS (likelihood of superiority) — вероятность того, что конкретная версия играет сильнее GreKo 2015 с учётом доверительного интервала расчёта рейтинга.
| Версия | GreKo 2015 | Fruit 2.1 | Delfi 5.4 | Crafty 23.4 | Kiwi 0.6d | Рейтинг | LOS |
|---|---|---|---|---|---|---|---|
| GreKo 2015 | 33 | 40.5 | 39.5 | 73.5 | 2600 | ||
| A | 53.5 | 38 | 49.5 | 46.5 | 76 | 2637 | 97% |
| B | 55 | 43.5 | 71 | 36.5 | 78.5 | 2667 | 99% |
| C | 52.5 | 39.5 | 81 | 42.5 | 75 | 2672 | 99% |
| D | 42 | 23.5 | 58 | 33.5 | 68 | 2574 | 7% |
| E | 53.5 | 37 | 51.5 | 46 | 81.5 | 2646 | 99% |
| F | 59 | 36.5 | 63 | 31.5 | 79.5 | 2648 | 98% |
| G | 48 | 24.5 | 59 | 43.5 | 65.5 | 2602 | 54% |
| H1 | 45.5 | 40 | 51.5 | 40.5 | 75.5 | 2616 | 81% |
| H2 | 55 | 33.5 | 65 | 39 | 74 | 2646 | 99% |
Видно, что улучшение игры произошло во всех случаях, кроме одного (версия D). Также интересно, что обучение на партиях гроссмейстеров (версия G) дало незначительный эффект. А вот добавление к партиям гроссмейстеров собственных игр программы плюс модификация стоимостей фигур (версия H2) оказалось достаточно удачной комбинацией.
Сильнейшей же по совокупности результатов оказалась версия C, с прибавкой в рейтинге порядка 70 пунктов. Для данного количества партий этот перевес статистически значимый, погрешность составляет плюс-минус 30 пунктов.
Мы обучали и тестировали программу на ультракоротком контроле времени, когда одна партия длится несколько секунд. Проверим, насколько наши улучшения сработают в «серьёзной» игре, с более длительными контролями.
| Контроль времени | Число партий | Результат | Рейтинг | LOS |
|---|---|---|---|---|
| 1 мин. + 1 сек. / ход | 200 | 116.5 — 83.5 | + 56 | 99% |
| 3 мин. + 2 сек. / ход | 100 | 57.5 — 42.5 | + 45 | 94% |
| 5 мин. на 40 ходов | 100 | 53.5 — 46.5 | + 21 | 77% |
Итак, несмотря на некоторое падение эффективности с увеличением длительности партий, обученная версия определённо демонстрирует более сильную игру, чем движок с оригинальным вариантом настроек. Она и была выпущена в качестве ещё одного финального релиза программы.
GreKo 2015 ML
Программу GreKo 2015 ML можно свободно скачать вместе с исходным кодом на C++. Она представляет собой консольное приложение под Windows или Linux. Для игры с человеком, анализа или спарринга с другими движками вам может понадобиться графический интерфейс — например, Arena, Winboard, или какой-либо ещё. Впрочем, можно играть и непосредственно из командной строки, вводя ходы стандартной англоязычной нотацией.
Функция самообучения в GreKo реализована как встроенная команда консольного режима (автору в данный момент неизвестны другие движки, поддерживающие подобную функциональность). Вектор из 27 коэффициентов оценочной функции хранится в файле weights.txt. Для его автоматической подстройки на базе PGN-файла нужно набрать команду learn, например:
White(1): learn gm2600.pgn
Программа прочитает все партии из указанного файла, создаст промежуточный файл с позициями для обучения и разобьёт его на тренировочное и тестовое подмножества:
Creating file 'gm2600.fen'
Games: 27202
Loading positions...
Training set: 1269145
Validation set: 317155
Затем сохранит исходные значения параметров в файл weights.old, и приступит к процессу оптимизации. Во время работы на экран и в файл learning.log выдаются промежуточные значения весов и целевого функционала.
Old values saved in file 'weights.old'
Start optimization...
0 0.139618890118 0.140022159883 2016-07-21 17:01:16
Parameter 6 of 27: PawnDoubled = -10
Parameter 7 of 27: PawnIsolated = -19
1 0.139602240177 0.140008376153 2016-07-21 17:01:50 [1.7] -20
2 0.139585446564 0.139992945184 2016-07-21 17:01:58 [1.7] -21
3 0.139571113698 0.139980624436 2016-07-21 17:02:07 [1.7] -22
4 0.139559690029 0.139971803640 2016-07-21 17:02:15 [1.7] -23
5 0.139552067028 0.139965861844 2016-07-21 17:02:23 [1.7] -24
6 0.139547879916 0.139964477620 2016-07-21 17:02:32 [1.7] -25
7 0.139543242843 0.139961056939 2016-07-21 17:02:40 [1.7] -26
8 0.139542575174 0.139962314286 2016-07-21 17:02:48 [1.7] -27
Parameter 8 of 27: PawnBackwards = -5
9 0.139531995624 0.139953185941 2016-07-21 17:03:04 [1.8] -4
10 0.139523642489 0.139947035972 2016-07-21 17:03:12 [1.8] -3
11 0.139518695795 0.139943580937 2016-07-21 17:03:21 [1.8] -2
12 0.139517501456 0.139943802704 2016-07-21 17:03:29 [1.8] -1
Parameter 9 of 27: PawnCenter = 9
Parameter 10 of 27: PawnPassedFreeMax = 128
13 0.139515067927 0.139941456600 2016-07-21 17:04:00 [1.10] 129
14 0.139500815202 0.139927669884 2016-07-21 17:04:08 [1.10] 130
...
По окончании обучения файл weights.txt будет содержать уже новые значения весов, которые вступят в силу при следующем запуске программы.
Команда learn может содержать ещё два аргумента, нижнюю и верхнюю границы интервала оптимизации. По умолчанию они равны 6 и 27 — т.е. оптимизируются все признаки, кроме стоимости фигур. Чтобы включить полную оптимизацию, следует указать границы явно:
White(1): learn gm2600.pgn 1 27
Алгоритм рандомизирован (в части разбиения на обучающую и тестовую выборки), поэтому при разных запусках могут получаться неодинаковые вектора коэффициентов.
Выводы
Для настройки оценочной функции мы использовали самообучение программы (reinforcement learning). Наилучшие результаты были достигнуты при анализе игр программы против самой себя. Фактически, единственным источником шахматных знаний выступала дебютная книга оболочки, необходимая для рандомизации игравшихся партий.
Нам удалось увеличить прогнозирующую способность оценки, что привело к статистически достоверному увеличению силы игры на разных контролях времени как с предыдущей версией, так и с набором независимых оппонентов. Улучшение составило 50...70 пунктов Эло.
Стоит отметить, что результат был достигнут на достаточно скромных объёмах: порядка 20 тыс. партий и 1 млн. позиций (для сравнения: AlphaGo обучалась на 27 миллионах позиций из партий с сервера, не считая дальнейших игр с самой собой). Оценочная функция GreKo также весьма несложная, включает всего 27 независимых параметров. У сильнейших шахматных движков их счёт может идти на сотни или тысячи. Тем не менее, даже в таких условиях методы машинного обучения привели к успеху.
Дальнейшее усовершенствование программы могло бы включать добавление новых критериев к оценочной функции (в частности, учёт стадии игры для всех рассмотренных параметров) и использование более продвинутых методов многомерной оптимизации (например, поиск глобальных экстремумов). В настоящий момент, однако, планы автора в данном направлении ещё не определены.
Ссылки
- Определяем веса шахматных фигур регрессионным анализом — вводная статья о модели оценки материала.
- GreKo — шахматная программа GreKo, обучением которой мы в этой статье занимались.
- Texel's Tuning Method — описание базового метода оптимизации оценочной функции.
- Mastering the Game of Go with Deep Neural Networks and Tree Search (англ.) — оригинальная статья об AlphaGo в Nature.
- AlphaGo на пальцах — изложение основных принципов устройства AlphaGo на русском языке.
- Giraffe: Using Deep Reinforcement Learning to Play Chess (англ.) — статья о шахматной программе Giraffe.
- bayeselo — утилита для расчёта рейтингов на основе PGN-файлов.
Автор: WinPooh73
