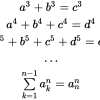Нам представилась замечательная возможность провести небольшое, но крайне поучительное тактическое занятие.
Вопросы оптимизации программ, производящих значительное количество вычислений, к сожалению, недостаточно хорошо освещены в литературе и, как правило, сводятся в некоторым общим принципам, верность которых совершенно не очевидна ни до прочтения аргументов автора, не даже после. Поскольку в упомянутом посте (ищите по закавыченным словам) была предложена не-безынтересная вычислительная задача, которая позволяет продемонстрировать эти принципы и конкретные приемы оптимизации в действии, и был создан настоящий пост, который, хоть и несколько отклоняется от направления, излюбленного автором (я вполне себе вижу решение данной задачи на МК класса М3 и даже Ардуино, попробуйте, но все таки микроконтроллеры предназначены несколько для других целей), но тем не менее вписывается в концепцию курса по программированию МК.
Итак, мы начинаем.
Напомню задачу — требуется найти пять целых неотрицательных чисел, таких, что сумма пятых степеней первых четырех из них равна пятой степени последнего. Формулировка не вполне корректная и будет в дальнейшем уточняться, но для начала сойдет. Естественный алгоритм решения этой задачи будет состоять в переборе возможных наборов чисел и проверке выполнения для них данного условия. Сразу же уточним условие — чисел, не превосходящих некоторой границы, иначе перебор может никогда не закончится, если такого набора вообще не существует (мы же не надеемся всерьез проверить ВСЕ наборы по пять из целых неотрицательных чисел, не знаю, как читатели, я то точно не доживу до окончания перебора). Напишем это естественное решение, чтобы сразу отметить одну важную черту современного программирования, и вот оно.
Сразу договоримся, что мы запускаем все свои программы в компиляторе MinGW версии 6.2 на х86 машине i3-2120 3.3 ГГц, что бы эти цифры не обозначали. Если у вас параметры системы отличаются от моих, то и абсолютные значения временных показателей будут несколько другими, хотя относительное время работы разных вариантов должно быть близко.
Что мы видим — среди наборов чисел, меньших 100, набора, отвечающего заданному условию, не найдено ( на самом деле найдено и их много, но они нас не устраивают, поскольку числа должны быть разными и не равными нулю… я об этом раньше не сказал? — еще один аргумент в пользу аккуратного формулирования ТЗ) и в процессе перебора мы проверили 1е10 комбинаций. При этом время работы программы составило 63 сек.
Мы уже поняли, что программа неверна в силу неполного формирования условий, но, прежде чем мы начнем ее модифицировать, поговорим о возможном ускорении вычислений при неизменном алгоритме. В мое время были книги, в которых давались рекомендации по машинно-независимой оптимизации исполнения по времени, и для данного алгоритма подошли бы следующие рекомендации:
— вынести часть вычислений из внутреннего цикла и сформировать промежуточную сумму первых трех чисел;
— организовать внутренний цикл по уменьшению индекса, а не возрастанию;
— организовать внутренний цикл в виде do {} while, а не for;
— сделать индексную переменную регистровой;
— оптимизировать вычисление пятой степени, что сократит число умножений с 4 до 3,
— перемежать вычисления степеней, чтобы не блокировать конвейер и так далее…
и первоначально я собирался все эти изменения провести и показать их влияние на быстродействие и продемонстрировать, как десятки процентов превращаются в разы увеличения быстродействия, но потом от этой идеи отказался.
Дело в том, что эти рекомендации несколько устарели и в настоящее время единственное, что от программиста требуется, так это разрешить компилятору провести оптимизацию на уровне 3. Да, нужно знать, как это сделать, в моем случае управление оптимизацией прячется в разделе Project/Settingы…-Compile/Optimization, но это все, что необходимо знать для проведения подобной оптимизации. Постоянные читатели моих постов (льщу себя надеждой, что такие есть) уже привыкли видеть в моих опусах стенания по поводу упадка нравов и недостаточно зеленой травы в современной электронике по сравнению с временами моего входа в профессию, но сейчас я, нисколько не отказываясь от высказанных ранее мнений, должен со всей определенностью заявить — современные компиляторы намного лучше своих предшественников и почти идеальны с точки зрения порождаемого кода, если им разрешить оптимизацию.
Столь сильное утверждение требует доказательства и вот оно — компилируем нашу программу с включенной оптимизацией и на том же самом процессоре видим время исполнения 20 секунд, то есть рост быстродействия в 3 раза (в основном за счет первой рекомендации, хотя остальные тоже дали свой вклад до пятой части ускорения) и без малейших усилий с нашей стороны — потрясающе. Желающие могут попробовать провести все перечисленные мною способы увеличения быстродействия и посмотреть на результат, но я настоятельно рекомендую просто посмотреть на продуцируемый ассемблерный код и понять, что улучшить его практически невозможно. Присоединяясь к автору исходного поста, могу настоятельно рекомендовать сайт gcc.godbolt.org, который дает возможность посмотреть код, порождаемый компилятором gcc для разных архитектур и для разных режимов оптимизации.
Увеличения быстродействия существенное, тема алгоритмо-независимой оптимизации исчерпана, но пост на этом не заканчивается — неужели есть еще что проделать. Да, есть чем и как улучшить программу (повысить ее быстродействие) и здесь компилятор нам уже не помощник, поскольку он не понимает сути производящихся в коде действий и не может предложить необходимых изменений, это может сделать только программист. На мой взгляд, это удача, раз даже современные средства разработки программ оставляют место для творчества, хотя мой молодой коллега нашел определенные неудобства в продвинутости современных компиляторов, заявив ;«Вам было проще, Вы знали, что компилятор ничего оптимизировать не будет, на него не надеялись и все делали вручную, а нам приходится решать, с какого момента начинается наша часть работы». Ну что сказать — если Вы сделаете ручками все необходимые оптимизации, то хуже точно не будет (лучше тоже не станет, поскольку работа будет задублирована), так что Вам ничто не мешает идти до конца, я всего лишь подсказал более короткую дорогу.
Возвращаемся к нашей программе и ищем способы ускорить ее. Вернее, прежде чем искать такие способы, необходимо удостоверится в необходимости данного действия. Проверяем время выполнения при разных значениях границы и обнаруживаем, что для значений 60 и 70 времена отличаются более, чем в 2 раза, что подтверждает нашу гипотезу относительно времени работы алгоритма как о(N**5): 70/60=1.17**5=2.2 раза. Воспользуемся полученной формулой для оценки времени выполнения нашей программы для границы 1000 и получим 553 часа, что несколько превосходит наши ожидания, для больших чисел время меньше точно не будет — есть смысл оптимизировать.
Далее перед абзацами будут указаны принципы решения инженерных задач системы ТРИЗ, как я ее помню.
ПРИНЦИП ИСКЛЮЧЕНИЯ, ИЛИ УБИРАЕМ ПОВТОРНУЮ РАБОТУ.
Пока мы не видим возможность изменить полученную оценку времени исполнения алгоритма, но можно уменьшить коэффициент при определяющем члене. Видно, что мы перебираем все перестановки заданного множества натуральных чисел, если учесть возможность их ранжировать и независимость результата от порядка операндов, то приходим к выводу, что нам необходимо рассматривать сочетания элементов заданного множества. Перебор сочетаний легко реализуется изменением начального значения переменной цикла для очередного элемента, что мы и проделываем и скорость работы программы возрастает разительно, на два порядка. Ну так и должно быть, мы рассчитывал на прирост в 5! раз, а это именно 120.
Небольшое отступление — в оригинальном посте автор приходит к подобной идее после выписывания на листочке различных комбинаций индексов и рассмотрения получившихся результатов, поскольку честно признается, что в комбинаторике не силен. Отдавая дань уважения его усилиям, должен заявить, что комбинаторика и элементы теории вероятностей (именно элементы, поскольку ТерВер во всей его красе и мощи не назовешь простым) — это та часть математики, без которой заниматься анализом алгоритмов контрпродуктивно. Я, конечно, рад, что автору удалось воссоздать метод генерации сочетаний, но его просто надо знать и все, как таблицу умножения. Это я по поводу периодически возникающих споров на тему, нужна ли программисту математика, но это мое личное мнение, выраженное в частной беседе, и оно может быть ошибочным.
Возвращаясь к основной теме — это именно та оптимизация, которую не сделает компилятор, поскольку тут нужно понимать суть задачи и реализующего ее решение алгоритма, а он на это пока не способен (компилятор с двумя командами все еще остается нереализованным идеалом, хотя кто знает, что будет дальше). И еще одна важная особенность — обычно выгода от подобной оптимизации многократно превышает любую возможную выгоду от оптимизации, осуществляемой компилятором, что и подтверждается в данном случае, поскольку 120>>5. Сведем полученные результаты и попытаемся экстраполировать их до некоторых больших значений, получаем
Граница__Без оптимизации____Компилятор______Наша________Обе
10_________0.00 _____________0.00__________0.00________0.00
50_________2.32______________0.66__________0.02________0.01
100________62.91_____________19.93_________0.49________0.16 ( 1.43)
150_______476.20____________150.67_________3.80________1.21 (10.99)
1000_______1800 ч*____________553 ч*_________14 ч*_______5 ч*(35 ч*)
(в скобках дано время вычислений для типа результата long long).
Видим, что если исходный вариант был практически неприемлем при значениях границы выше 200, то последний вариант применим до значения 1000. И мы даже нашли решение, причем целых два, правда, одно из них ложное из-за переполнения, но об этом чуть позже, а пока попытаемся еще улучшить быстродействие.
ПРИНЦИП ПРЕДВАРИТЕЛЬНОГО ИСПОЛНЕНИЯ.
Очевидное решение — вычислить значения степеней заранее и выбирать его из таблицы, несомненно, дало результат, но, честно говоря, несколько меньший, чем я надеялся, видимо, с реализацией умножения у х86 все хорошо, а вот с выбором из массива хуже. Но все равно, прирост почти в 8 раз – очень приятно. (Почему то для варианта с типом результата int прироста производительности вообще нет). Чисто теоретически, я могу себе представить компилятор, который подобную оптимизацию проведет, но пока я такого не видел. Обратим внимание на то, что в данном случае нам пришлось за быстродействие заплатить дополнительной памятью, что характерно, поскольку два направления оптимизации — по времени и по памяти, как правило, противоречат друг другу.
#include "time.h"
#include "stdio.h"
#define LOOP(n,m) for (int n=m+1; n<=MAX; n++)
#define REZ(i) (Pow5[i])
typedef long long int rez_t;
int main(void) {
rez_t Pow5[1001];
for (int i=0; i<=1000; i++) Pow5[i]=(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i;
for (int MAX=50; MAX<=500; MAX+=50) {
clock_t t = clock();
unsigned long long v=0;
int r=0;
LOOP(i1,0)
LOOP(i2,i1)
LOOP(i3,i2) {
rez_t Sum = REZ(i1)+REZ(i2)+REZ(i3);
LOOP(i4,i3)
LOOP(i5,i4)
{
v++;
if (Sum+REZ(i4)==REZ(i5)) {
r++;
printf("%4d %4d %4d %4d %4d n",i1,i2,i3,i4,i5);
};
};
};
t = clock() - t;
printf ("MAX=%d time is %f seconds.n",
MAX, ((double)t)/CLOCKS_PER_SEC);
printf(" %llu %dn",v,r);
};
return 1;
};
ПРИНЦИП ОГРАНИЧЕНИЯ, ИЛИ ИСКЛЮЧАЕМ НЕПОДХОДЯЩИЕ ВАРИАНТЫ.
Идем дальше и ищем дополнительные пути, для чего несколько переформулируем задачу — нам нужно найти число, пятая степень которого равна некоторому конкретному числу (представляющему собой сумму пятых степеней четырех других чисел, но это неважно). Данная формулировка позволяет нам сосредоточится на слове «найти» и сразу же наталкивает на мысль о направлении оптимизации — ускорении поиска, у нас он был линейный путем перебора всех возможных значений, а это не лучший способ для упорядоченного набора данных. Первая мысль — бинарный поиск и такое направление могло бы дать нам существенный прирост производительности, но мы пойдем другим путем — для начала перестанем просматривать варианты, которые заведомо не могут быть решением, поскольку мы перебираем значения в порядке возрастания и искомое значение уже превышено. Можно ожидать прироста скорости раза в два, точная аналитическая оценка едва ли возможна и мы действительно получаем ускорение почти в 5 раз.
Небольшое замечание — для того, чтобы перейти к этому методу нам пришлось изменить тип результата на двойное целое. Дело в том, что предложенный метод требует упорядоченности пятых степеней чисел-кандидатов, а из равенства n>m, к моему глубочайшему сожалению, не следует n%k > m%k, если любое из n или m превосходит k. Вы спросите, откуда тут взялось k, ведь мы просто работаем с целыми числами, но дело в том, что в любой практически реализуемой архитектуре целые числа (если скорость выполнения арифметических операция с ними разумна) имеют ограниченную разрядность и, соответственно, подразумевают взятие результата каждой операции по модулю максимально представимого числа. Если у нас результат 32 разрядный, то это число составит (2**32)-1 ~ 2**32 = (2**2)*(2**30) = 4*((2**10)**3) ~ 4*((10**3)**3) = 4*(10**9) = 0.4*(10**10) и корень пятой степени из этого числа составит число, близкое к 100 (точное значение 84). тогда для 64 разрядного результата получим наибольшее значение границы 7130, а для 128 разрядного ~ 50е6.
#include "time.h"
#include "stdio.h"
#define LOOP(n,m) for (int n=m+1; n<=MAX; n++)
#define REZ(i) (Pow5[i])
typedef long long rez_t;
int main(void) {
rez_t Pow5[1001];
for (int i=0; i<=1000; i++) Pow5[i]=(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i;
for (int MAX=50; MAX<=500; MAX+=50) {
clock_t t = clock();
unsigned long long v=0;
int r=0;
LOOP(i1,0)
LOOP(i2,i1)
LOOP(i3,i2) {
rez_t Sum3 = REZ(i1)+REZ(i2)+REZ(i3);
int i4=i3+1;
do {
rez_t Sum4 = Sum3 + REZ(i4);
int i5=i4+1;
do {
v++;
if (Sum4==REZ(i5)) {
r++;
printf("%4d %4d %4d %4d %4d n",i1,i2,i3,i4,i5);
};
i5++; } while ((Sum4>=REZ(i5)) && (i5<=MAX));
i4++; } while (i4<=MAX);
};
t = clock() - t;
printf ("MAX=%d time is %f seconds.n",
MAX, ((double)t)/CLOCKS_PER_SEC);
printf(" %llu %dn",v,r);
};
return 1;
};ПРИНЦИП ОЦЕНОК, ИЛИ ИСПОЛЬЗУЕМ ПРЕДЫДУЩИЕ РЕЗУЛЬТАТЫ (ГУСЕНИЦА).
Неплохо, хотя для бинарного поиска должно быть намного лучше, но мы учитываем еще одно соображение, которое делает такой способ предпочтительнее — мы можем существенно сократить время поиска, если не будем просматривать числа, меньшие найденного в предыдущем цикле, ведь раз они были меньше предыдущей суммы, то гарантированно будут меньше текущей, которая предыдущую превосходит. Получается, что мы можем работать по принципу гусеницы («Caterpillar method») для четвертого и пятого числа, а при применении данного метода гарантированное количество итераций не может превзойти значения 2*n, где n — длина интервала и мы по сравнению с предыдущим необходимым количеством итераций n*(n-1)/2 выигрываем в (n-1)/4 раз, что весьма и весьма значительно для больших чисел. При этом количество итераций даже лучше, чем для бинарного поиска, которое составит n*log2(n) и превзойдет наше значение уже при n>2**2=4.
#include "time.h"
#include "stdio.h"
#define LOOP(n,m) for (int n=m+1; n<=MAX; n++)
#define REZ(i) (Pow5[i])
typedef long long rez_t;
int main(void) {
rez_t Pow5[1001];
for (int i=0; i<=1000; i++) Pow5[i]=(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i;
for (int MAX=50; MAX<=500; MAX+=50) {
clock_t t = clock();
unsigned long long v=0;
int r=0;
LOOP(i1,0)
LOOP(i2,i1)
LOOP(i3,i2) {
rez_t Sum3 = REZ(i1)+REZ(i2)+REZ(i3);
int i4=i3+1;
int i5=i4+1;
do {
rez_t Sum4 = Sum3 + REZ(i4);
if (Sum4 >= REZ(i5)) do {
v++;
if (Sum4==REZ(i5)) {
r++;
printf("%4d %4d %4d %4d %4d n",i1,i2,i3,i4,i5);
};
i5++; } while ((Sum4>=REZ(i5)) && (i5<=MAX));
i4++; } while ((i4<=MAX) && (i5<MAX));
};
t = clock() - t;
printf ("MAX=%d time is %f seconds.n",
MAX, ((double)t)/CLOCKS_PER_SEC);
printf(" %llu %dn",v,r);
};
return 1;
};
Замечательный факт — нам впервые удалось понизить не коэффициент перед определяющим членом, а порядок его, что приводит к весьма существенному ускорению работы для больших значений границ рассматриваемых чисел. Сведем еще раз результаты в таблицу и порадуемся полученным значениям
Граница__Таблица степеней___Ограничение 5__Метод гусеницы__Метод инверсии
100________0.3_________________0.1__________0.02____________0.04
150________1.8_________________0.6__________0.14____________0.28
200________6.6_________________2.3__________0.49____________0.36
300_______50.4________________16.1__________2.14____________2.26
1000_______6 ч*________________1.5 ч*_______210.0____________880*
5000_______2 г*________________0.5 г*________36 ч*
Дальнейшие расчеты показывают, что мы можем ожидать получение результата для границы 10 тысяч в течении 24 дней, что практически приемлемо, хотя этого мы делать и не будем.
Дальнейшее рассмотрение темы планировалось с учетом замечательного свойства пятой степени, а именно небольшого числа остатков по модулю 11, но эта тема неплохо раскрыта в очередном посте на тему гипотезы Эйлера и повторяться не буду, замечу только, что простого способа использования данного свойства предложено не было (и я его не вижу) а непростые требуют прямо таки неприличного количества памяти.
МЕТОД ИНВЕРСИИ.
Поэтому рассмотрение вопроса продолжим с другой стороны — переформулируем задачу следующим образом — найти четыре натуральных числа, сумма пятых степеней которых составит пятую степень натурального числа. На первый взгляд, ничего особенного не произошло, но мы можем начать задачу с конца — задаемся искомой суммой и пытаемся ее составить. Такой подход сразу позволяет нам сформулировать некоторые ограничения на подходящие числа. Например, для наибольшего из четырех чисел мы знаем, что оно не может превосходить искомого числа (это тривиально) и его пятая степень не может быть меньше одной четвертой пятой степени искомого числа (а вот это не столь тривиально, но очевидно), что сужает область допустимых кандидатов с n-1 до n*(1-корень пятой степени из 4=1.32), то есть в три раза. Далее, взяв кандидата на роль четвертого числа, мы можем сразу вычислить оставшуюся разность и выбирать кандидата на роль третьего числа с учетом аналогичных соображений по отношению к ней. Оценить результат подобной оптимизации аналитически лично я не берусь, поэтому просто пишем программу и смотрим на результат.
#include "time.h"
#include "stdio.h"
#define LOOP(n,m) for (int n=m+1; n<=MAX; n++)
#define REZ(i) (Pow5[i])
typedef long long rez_t;
int main(void) {
rez_t Pow5[1001];
for (int i=0; i<=1000; i++) {
Pow5[i]=(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i;
};
for (int MAX=100; MAX<=1000; MAX+=50) {
clock_t t = clock();
unsigned long long v=0;
int r=0;
int i5=MAX; do {
int i4=i5-1;
do {
rez_t Ost1=REZ(i5)-REZ(i4);
int i3=i4-1;
if (REZ(i4)*4 > Ost1)
do {
rez_t Ost2 = Ost1-REZ(i3);
int i2=i3-1;
if ((REZ(i3)*3 > Ost2) && (Ost2>0))
do {
rez_t Ost3=Ost2-REZ(i2);
int i1=i2-1;
if ((REZ(i2)*2 > Ost3) && (Ost3>0))
do {
v++;
if (Ost3==REZ(i1)) {
r++;
printf("%4d %4d %4d %4d %4d n",i1,i2,i3,i4,i5);
};
i1--; } while (i1>0);
i2--; } while (i2>0);
i3--; } while (i3>0);
i4--; } while (i4>0);
i5--;} while (i5>0);
t = clock() - t;
printf ("MAX=%d time is %f seconds.n",
MAX, ((double)t)/CLOCKS_PER_SEC);
printf(" %llu %dn",v,r);
};
return 1;
};Неплохо, нам удалось существенно уменьшить коэффициент, но порядок остался прежним и на больших значениях мы проигрываем предыдущей программе.
И тут приходит озарение – мы можем начать по новому методу, существенно сократив перебор двух старших слагаемых, а два младших будем искать методом гусеницы, поскольку мы уже знаем их сумму!!! (Количество восклицательных знаков вполне соответствует мощности идеи). То есть мы возьмем младшее число равным единице, следующее – максимально возможному с учетом старших и будем двигать нижнюю либо верхнюю границу интервала в зависимости от результата.
#include "time.h"
#include "stdio.h"
#define LOOP(n,m) for (int n=m+1; n<=MAX; n++)
#define REZ(i) (Pow5[i])
typedef long long rez_t;
int main(void) {
rez_t Pow5[1001];
for (int i=0; i<=1000; i++) {
Pow5[i]=(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i*(rez_t)i;
};
for (int MAX=100; MAX<=1000; MAX+=50) {
clock_t t = clock();
unsigned long long v=0;
int r=0;
int i5=MAX; do {
int i4=i5-1;
do {
rez_t Ost1=REZ(i5)-REZ(i4);
int i3=i4-1;
if (REZ(i4)*4 > Ost1)
do {
rez_t Ost2 = Ost1-REZ(i3);
int i2=i3-1;
int i1=1;
if ((REZ(i3)*3 > Ost2) && (Ost2>0))
do {
v++;
rez_t Sum2=REZ(i1)+REZ(i2);
if (Ost2==Sum2) {
r++;
printf("%4d %4d %4d %4d %4d n",i1,i2,i3,i4,i5);
};
if (Sum2>=Ost2) i2--; else i1++;
} while (i1<=i2);
i3--; } while (i3>0);
i4--; } while (i4>0);
i5--;} while (i5>0);
t = clock() - t;
printf ("MAX=%d time is %f seconds.n",
MAX, ((double)t)/CLOCKS_PER_SEC);
printf(" %llu %dn",v,r);
};
return 1;
};Вот программа, а вот и результат – для значений до тысячи мы считаем всего лишь 21.7 секунды – в 10 раз быстрее предыдущей версии, а уж с начальной и сравнивать не будем. С такой программой можно уже замахиваться и на значения порядка тысяч, оставляю это на долю пытливого читателя.
Всех с Новым годом.
Автор: GarryC