Как известно, OpenGL версии 1 позволяет использовать не менее восьми штатных источников света. Используя эти источники можно достаточно просто строить качественное цветное освещение без применения карт освещённости. Как оказалось, при разработке самодельных простейших трёхмерных движков, их авторам эта возможность не кажется очевидной и потому ими игнорируется. Описанный ниже способ не подходит для перемещающихся в пространстве источников света, но отлично подходит, если остальные параметры источника света изменяются во времени (например, изменяется цвет источника освещения, или он мигает). Как построить качественное освещение с использованием штатных источников освещения OpenGL и будет рассказано в статье.
Должен сказать, что статья эта планировалась очень давно – года так с 2004, когда был написан трёхмерный движок, использующий описываемый метод. Однако, обилие формул и лень заставили меня уже в скором времени забросить написание статьи. Последний раз я касался текста в 2008 году. На этой дате статья и остановилась, и возрождать я её не планировал. Но недавно, в теме про исходники Quake 2, меня попросили всё же рассказать о применённой в моём трёхмерном движке технологии построения картинки. Актуальность столь запоздавших статей для современного программирования трёхмерной графики, конечно, нулевая, но возможно, начинающим изучать OpenGL эта статья будет интересна.
Для начала я покажу, какие именно получаются изображения при применении описываемого метода. Вот скриншоты моего движка 2004 года:

Скриншоты трёхмерного движка.
Как видите, для простейшего движка получаются достаточно красивые картинки.
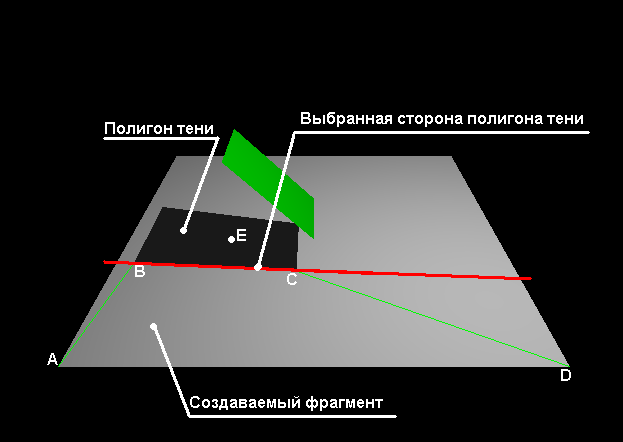
Идея алгоритма заключается в том, что многоугольник, источник тени (в дальнейшем – МИТ), своей тенью разбивает многоугольник, приёмник тени (в дальнейшем – МПТ) на фрагменты A, B, C, D, E, как показано на рисунке ниже. Можно заметить, что для фрагментов A, B, E, D источник света включён, а для фрагмента C источник света отключён
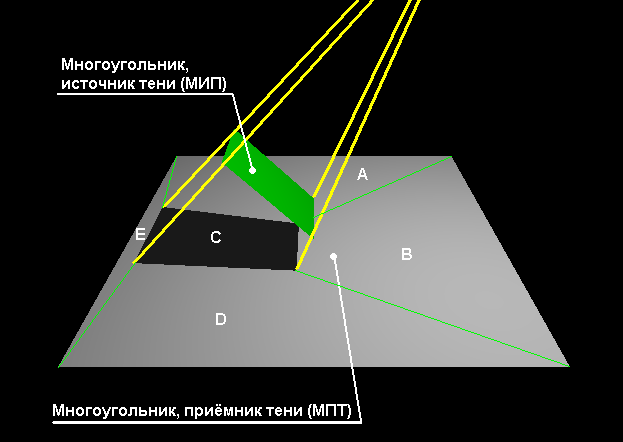
Разбиение на фрагменты тенью.
Общий алгоритм построения освещения таков:
- Выбираем источник света.
- Каждый многоугольник сцены разбиваем на фрагменты многоугольником, который может отбрасывать тень. При этом вновь получившиеся фрагменты будут являться новыми многоугольниками сцены, на которые нужно будет вновь построить тени от других многоугольников (но которые сами не будут источниками теней – бессмысленно использовать для построения тени части вместо исходного целого многоугольника). Такую операцию необходимо провести для всех многоугольников сцены.
- Переходим на шаг 1 для следующего источника света.
В результате такого разбиения мы получим для каждого исходного многоугольника набор фрагментов, для каждого из которых известно, какие источники света его освещают. На практике это означает, что при выводе этих фрагментов движок должен включать или отключать источники света, для которых точно известно, что они данный фрагмент не освещают.
Поскольку мы используем только восемь источников света OpenGL, то при разбиении сцены можно просто выбрать только те источники из общего списка источников света, которые максимально сказываются на выбранном многоугольнике сцены. В самом простом случае это можно сделать, например, посчитав расстояние от источника до вершин многоугольника и выбрать источники с минимальными расстояниями до вершин. Конечно, в этом случае часть источников могут оказаться бесполезными для выбранного многоугольника (источник может вообще быть полностью загорожен другим многоугольником), но зато алгоритм выбора очень прост.
Как видите, метод несложный, однако, потребует алгоритма построения фрагментов, зная МИТ, МПТ и положение источника света.
Реализация алгоритма
Условимся считать все многоугольники выпуклыми. Есть это не так, их следует разбить на выпуклые части. Для реализации алгоритма нахождения фрагментов нам понадобятся некоторые функции, а именно:
Функция, определяющая позицию точки относительно некоторой плоскости.
Входные данные:
— Точка плоскости $inline$P(P_{x},P_{y},P_{z})$inline$;
— Вектор нормали к плоскости $inline$n(n_{x},n_{y},n_{z})$inline$;
— Точка, для которой определяется положение относительно плоскости $inline$V(V_{x},V_{y},V_{z})$inline$.
Возвращаемое значение: 1 — точка находится выше плоскости, -1 — точка находится ниже плоскости, 0- точка находится в плоскости.
Для реализации этой функции воспользуемся уравнением плоскости, тогда $inline$ begin{equation}t=n_{x}(V_{x}-P_{x})+n_{y}(V_{y}-P_{y})+n_{z}(V_{z}-P_{z})end{equation} $inline$ (1).
Полученное $inline$t$inline$ определяет положение точки $inline$V$inline$ относительно плоскости.
Функция должна возвращать -1, если $inline$t<0$inline$, возвращать 1, если $inline$t>0$inline$ и возвращать 0, если $inline$t=0$inline$.
Однако, мы работаем на разрядной сетке ЭВМ, поэтому сравнивать с нулём нельзя. Вместо этого мы будем здесь и далее сравнивать с некоторым малым $inline$varepsilon$inline$, значение которого проще всего подобрать опытным путём так, чтобы алгоритм не давал сбоев.
В этом случае функция должна возвращать -1, если $inline$t<-varepsilon$inline$, возвращать 1, если $inline$t>varepsilon$inline$ и возвращать 0 во всех остальных случаях.
Функция, определяющая точку пересечения прямой с плоскостью.
Входные данные:
— Точка плоскости $inline$P(P_{x},P_{y},P_{z})$inline$;
— Вектор нормали к плоскости $inline$n(n_{x},n_{y},n_{z})$inline$;
— Первая точка прямой $inline$A(A_{x},A_{y},A_{z})$inline$;
— Вторая точка прямой $inline$B(B_{x},B_{y},B_{z})$inline$;
Возвращаемое значение: координаты точки пересечения либо флаг, показывающий что пересечения нет.
Вектор $inline$L(L_{x},L_{y},L_{z})$inline$, задающий направление прямой вычисляется как $inline$ begin{array}{c}L_{x}=B_{x}-A_{x},\L_{y}=B_{y}-A_{y},\L_{z}=B_{z}-A_{z}.end{array} $inline$
Тогда скалярное произведение между вектором нормали и вектором прямой будет $inline$E=L_{x}cdot n_{x}+L_{y}cdot n_{y}+L_{z}cdot n_{z}$inline$.
Если $inline$E=0$inline$ (в нашем случае это условие примет вид $inline$Egeq-varepsilon$inline$ и $inline$Eleqvarepsilon$inline$ ), то прямая и плоскость пересекаться не могут, поскольку вектора перпендикулярны.
Если же пересечение возможно, то координаты точки пересечения могут быть получены по формулам
$$display$$begin{array}{c}V_{x}=A_{x}-L_{x}frac{t}{E}\V_{y}=A_{y}-L_{y}frac{t}{E},\V_{z}=A_{z}-L_{z}frac{t}{E}.end{array} $$display$$
где $inline$t$inline$ — значение, полученное по формуле (1).
Функция, определяющая точку пересечения луча с плоскостью.
Входные данные:
— Точка плоскости $inline$P(P_{x},P_{y},P_{z})$inline$;
— Вектор нормали к плоскости $inline$n(n_{x},n_{y},n_{z})$inline$;
— Первая точка луча (начало луча) $inline$A(A_{x},A_{y},A_{z})$inline$;
— Вторая точка луча $inline$B(B_{x},B_{y},B_{z})$inline$.
Возвращаемое значение: координаты точки пересечения либо флаг, показывающий что пересечения нет.
Задача сводится к предыдущей, но появляются дополнительные условия возможности пересечения, поскольку луч, в отличие от прямой, полубесконечен.
Так, если получится, что $inline$-t<E$inline$ для $inline$E>0$inline$ или $inline$t>E$inline$ для $inline$E<0$inline$ (в нашем случае $inline$-t<E+varepsilon$inline$ для $inline$E>0$inline$ или $inline$t>E-varepsilon$inline$ для $inline$E<0$inline$ ), то луч плоскость не пересекает.
Функция, определяющая, нахождение точки внутри выпуклого многоугольника, лежащего в плоскости.
Входные данные:
— Точки многоугольника, лежащие в одной плоскости $inline$P0(P0_{x},P0_{y},P0_{z})...Pn(Pn_{x},Pn_{y},Pn_{z})$inline$;
— Точка, находящаяся в плоскости многоугольника, для которой проверяется её нахождение внутри многоугольника $inline$V(V_{x},V_{y},V_{z})$inline$.
Возвращаемое значение: флаг, показывающий находится точка внутри многоугольника или нет.
Алгоритм работы функции выглядит так:
Введём переменную $inline$a$inline$=индекс последней точки многоугольника;
Цикл по $inline$i$inline$ от 0 до $inline$a$inline$;
Введём переменные индексов трёх последовательных точек $inline$i0=i$inline$,$inline$i1=i+1$inline$,$inline$i2=i+2$inline$;
Если $inline$i1>a$inline$, то $inline$i1=i1-a-1$inline$;
Если $inline$i2>a$inline$, то $inline$i2=i2-a-1$inline$;
Возьмём три последовательные точки многоугольника $inline$A=P(i0)$inline$,$inline$B=P(i1)$inline$,$inline$C=P(i2)$inline$;
Создадим три вектора: $inline$F(F_{x},F_{y},F_{z}),G(G_{x},G_{y},G_{z}),H(H_{x},H_{y},H_{z})$inline$ по формулам
$$display$$ begin{array}{c}F_{x}=B_{x}-A_{x},\F_{y}=B_{y}-A_{y},\F_{z}=B_{z}-A_{z}.end{array}$$display$$
$$display$$ begin{array}{c}G_{x}=C_{x}-A_{x},\G_{y}=C_{y}-A_{y},\G_{z}=C_{z}-A_{z}.end{array}$$display$$
$$display$$ begin{array}{c}H_{x}=V_{x}-A_{x},\H_{y}=V_{y}-A_{y},\H_{z}=V_{z}-A_{z}.end{array}$$display$$
Вычислим векторные произведения $inline$N1(N1_{x},N1_{y},N1_{z})=Ftimes G$inline$ и $inline$N2(N2_{x},N2_{y},N2_{z})=Ftimes H$inline$;
Вычислим скалярное произведение $inline$R=N1_{x}*N2_{x}+N1_{y}*N2_{y}+N1_{z}*N2_{z}$inline$;
Если $inline$R<0$inline$ (в нашем случае $inline$R<-varepsilon$inline$), то точка внутрь многоугольника не попадает.
Конец цикла;
Точка попадает внутрь многоугольника.
Идея работы функции заключается в том, что три подряд идущие точки многоугольника задают два ребра многоугольника, преобразовав которые в вектора, можно вычислить векторное произведение векторов первого ребра со вторым и первого ребра с вектором, составленным из первой точки многоугольника и исследуемой точкой.
При этом, направления получившихся векторов зависят от того, по какую сторону от первого ребра находится точка. Для вычисления согласованности получившихся векторов используется их скалярное произведение, которое будет отрицательным, если вектора направлены в противоположные стороны.
Алгоритм построения фрагментов
Входные данные:
— Точки $inline$PS(PS0_{x},PS0_{y},PS0_{z})...PSn(PSn_{x},PSn_{y},PSn_{z})$inline$ выпуклого многоугольника, являющегося источником тени), лежащие в одной плоскости;
— Точки $inline$PD(PD0_{x},PD0_{y},PD0_{z})...PDn(PDn_{x},PDn_{y},PDn_{z})$inline$ выпуклого многоугольника, на который отбрасывается тень), лежащие в одной плоскости;
-Точка положения источника света $inline$L(L_{x},L_{y},L_{z})$inline$ (далее по тексту ИС — «источник света»);
Возвращаемые данные: флаг, показывающий существует тень или нет, и массив многоугольников, на которые разбивается МПТ тенью.
Получение точек тени в плоскости МПТ
Рассмотрим алгоритм получения точек тени в системе координат МПТ.
- Проверим, что МИТ и МПТ имеют не менее трёх точек, иначе это, строго говоря, вообще не многоугольники, и тени нет.
- Проверим, может ли ИС освещать МПТ. Условимся, что если ИС лежит выше плоскости МПТ (нормаль МПТ направлена в сторону ИС), то он может освещать МПТ, иначе, это невозможно. Если ИС освещать МПТ не может, то тени нет.
- Поскольку МИТ может пересекать МПТ, то нужно скорректировать МИТ так, чтобы он всегда был выше МПТ. Для этого нужно пройтись циклом по рёбрам МИТ, оставляя точки, которые лежат выше плоскости МПТ и отбрасывая точки, лежащие ниже плоскости МПТ, причём, если точки какого-либо ребра находятся по разные стороны от плоскости, задаваемой МПТ, то нужно добавить к новому МИТ эти точки пересечения. Таким образом, у нас будет новый МИТ, лежащий точно выше МПТ. Если после коррекции точек МИТ меньше трёх, то тени нет.
- Возможна ситуация, когда МПТ и ИС находятся по одну сторону от МИТ. В этом случае тоже тени нет. Это можно проверить определив положение ИС относительно плоскости МИТ и сравнивая с этим положением положения точек МПТ относительно плоскости МИТ. Если хоть одна точка МПТ лежит по другую сторону плоскости МИТ, нежели ИС, то тень существует, иначе тени нет.
- Теперь нужно сформировать теневой объём. Всё, что попадает в теневой объём, ИС не освещается. Фигура, задающая теневой объём, ограничивается сверху МИТ, снизу её ничто не ограничивает (так как объём простирается в бесконечность), а по бокам её ограничивают четырёхугольные грани, у которых две вершины так же находятся в бесконечности, а две другие совпадают с вершинами ребра МИТ.
- Поскольку МИТ уже задан, то требуется найти четырёхугольные грани. Так как нам от этих граней нужно сейчас только то, что они задают плоскости, то заменим бесконечные вершины на конечные. Для этого возьмём рёбра МИТ, и пустим луч от ИС через вершины рёбер. Для примера возьмём первые две точки МИТ $inline$PS0$inline$ и $inline$PS1$inline$, тогда координаты точек грани теневого объёма $inline$V0,V1,V2,V3$inline$ определяются как
$$display$$begin{array}{l}V0_{x}=PS0_{x}+N0_{x};\V0_{y}=PS0_{y}+N0_{y};\V0_{z}=PS0_{z}+N0_{z};\V1_{x}=PS0_{x};\V1_{y}=PS0_{y};\V1_{z}=PS0_{z};\V2_{x}=PS1_{x};\V2_{y}=PS1_{y};\V2_{z}=PS1_{z};\V3_{x}=PS1_{x}+N1_{x};\V3_{y}=PS1_{y}+N1_{y};\V3_{z}=PS1_{z}+N1_{z},end{array}$$display$$
где
$$display$$begin{array}{l}N0_{x}=PS0_{x}-L_{x};\N0_{y}=PS0_{y}-L_{y};\N0_{z}=PS0_{z}-L_{z};\N1_{x}=PS1_{x}-L_{x};\N1_{y}=PS1_{y}-L_{y};\N1_{z}=PS1_{z}-L_{z}.end{array}$$display$$
Поскольку МИТ мог быть ориентирован как угодно, то нормали граней теневого объёма могут быть направлены как внутрь объёма, так и наружу. Условимся, что нормали теневого объёма должны быть направлены наружу.
Для этого сравним положение точки, точно попадающей в теневой объём относительно плоскостей, задаваемых гранями теневого объёма. Такая точка может быть получена, если найти геометрический центр МИТ
$$display$$begin{array}{l}x_{c}=frac{sum_{i=0}^{max}PSi_{x}}{max};\y_{c}=frac{sum_{i=0}^{max}PSi_{y}}{max};\z_{c}=frac{sum_{i=0}^{max}PSi_{z}}{max}.end{array}$$display$$
и пустить луч от ИС через этот центр, так же, как это делалось для нахождения вершин граней теневого объёма. Если при определении положения этой точки относительно плоскостей граней будет получено для какой-либо грани, что точка находится выше выбранной грани, то грань следует “перевернуть”, т.е. поменять знаки координат вектора нормали грани на противоположные. Направление обхода самих точек, задающих грань можно не менять, так как это в дальнейшем не понадобится.
- Теперь мы должны найти точки тени. Сначала мы найдём точки МПТ, лежащие внутри теневого объёма. Делается это так: каждую точку МПТ нужно сравнить со всеми плоскостями, задаваемыми гранями теневого объёма, и если окажется, что для всех граней она находится ниже плоскости грани (или в грани), то такая точка точно лежит внутри теневого объёма. После этого надо найти точки пересечения теневого объёма с МПТ. Для этого мы для каждой грани теневого объёма проходим по всем рёбрам МПТ и находим пересечения ребёр с плоскостью данной конкретной грани, проверяя, попадает ли точка пересечения внутрь теневого объёма. Однако, это ещё не все точки из которых может собираться тень. Нужны ещё точки пересечения граней теневого объёма с МПТ. Для того чтобы их найти, нам нужно вычислить точки пересечения плоскости МПТ и лучей, выходящих из ИС и проходящих через вершины МИТ, проверив, что все полученные точки лежат внутри МПТ. В конечном итоге, у нас должен получиться массив точек, из которых собирается тень на плоскости МПТ. Однако эти точки ещё не упорядочены.
- Дальше точки тени следует перевести в систему координат МПТ (будет плоскость XZ, где координата Y=0), то есть спроецировать на плоскость МПТ. Чтобы отсортировать точки тени, можно взять центр этих точек (считается как среднее арифметическое координат в плоскости) и отсортировать по углу (считается через арктангенс (atan2) координат) и расстоянию от центра.
- Теперь точки тени у нас упорядочены, пересчитаны в плоскость МПТ и пора строить фрагменты. Совершенно естественно, что первым фрагментом будет сама тень (если, конечно, она не стянулась в линию (с допуском по погрешности), что тоже возможно — в этом случае считаем, что тени нет). Теперь берём каждую сторону многоугольника тени и добавляем в фрагмент все те точки, которые находятся снаружи многоугольника тени (лежат с центральной точкой многоугольника тени по разные стороны от выбранной стороны многоугольника тени), как показано на рисунке. Кроме того, следует добавить и точки пересечения сторон МПТ и прямой, содержащей выбранную сторону многоугольника тени. Разумеется, одинаковые до погрешности по координатам точки добавлять не следует. После добавления всех точек во фрагмент, обрезаем МПТ по краям и повторяем операции со следующей стороной многоугольника тени.
Создание фрагмента
- Получив все фрагменты, пересчитываем их координаты обратно в трёхмерную систему координат, не связанную с МПТ.
Вот, собственно, и весь алгоритм. Все пункты с 1 по 10 можно посмотреть в файле shadow.cpp, находящегося в папке с демонстрационной программой Lighting.
В архиве по ссылке (опять не на github — я с ним пока ещё не подружился) присутствуют программы с исходниками:
- Демонстрационная программа Lighting, строящая в реальном времени тени от двух источников света на пирамидку и плоскость под ней.
- 3D-движок, использующий вышеописанную технологию.
- Редактор карт 3D-движка (целиком на Win32API, никакого OVL или MFC).
Автор: da-nie