Метод Уэлфорда — простой и эффективный способ для вычисления средних, дисперсий, ковариаций и других статистик. Этот метод обладает целым рядом прекрасных свойств:

• достигает отличных показателей по точности решений;
• его чрезвычайно просто запомнить и реализовать;
• это однопроходный онлайн-алгоритм, что крайне полезно в некоторых ситуациях.

Оригинальная статья Уэлфорда была опубликована в 1962 году. Тем не менее, нельзя сказать, что алгоритм сколь-нибудь широко известен в настоящее время. А уж найти математическое доказательство его корректности или экспериментальные сравнения с другими методами и вовсе нетривиально.

Настоящая статья пытается заполнить эти пробелы.

^[1]

Содержание

• Введение ^[2]
• 1. Погрешности при вычислении средних ^[3]
• 2. Обозначения ^[4]
• 3. Вычисление средних ^[5]
• 4. Вычисление ковариаций ^[6]
• 5. Экспериментальное сравнение методов ^[7]
• Заключение ^[8]

Введение

В первые месяцы своей деятельности в качестве разработчика я занимался созданием метода машинного обучения, в котором градиентному бустингу подвергались деревья решений с линейными регрессионными моделями в листьях. Такой алгоритм был выбран отчасти в пику модной тогда и победившей сегодня концепции строить огромные композиции очень простых алгоритмов: хотелось, напротив, строить небольшие композиции достаточно сложных моделей.

Сама эта тема оказалась настолько для меня интересной, что я потом даже диссертацию ^[9] про это написал. Для построения модели из нескольких сотен деревьев приходится решать задачу линейной регрессии десятки тысяч раз, и оказалось сложным достичь хорошего качества во всех случаях, ведь данные для этих моделей весьма разнообразны, и проблемы мультиколлинеарности, регуляризации и вычислительной точности встают в полный рост. А ведь достаточно одной плохой модели в одном листе одного дерева для того, чтобы вся композиция оказалась совершенно непригодной.

В процессе решения проблем, связанных с автоматическим построением огромного количества линейных моделей, мне удалось узнать некоторое количество фактов, которые пригодились мне в дальнейшем в самых разных ситуациях, в том числе не связанных с собственно задачей линейной регрессии. Теперь хочется рассказать о некоторых из этих фактов, и для начала я решил рассказать о методе Уэлфорда.

У статьи следующая структура. В пункте 1 ^[3] мы рассмотрим простейшую задачу вычисления среднего, на примере которой поймём, что эта задача не так уж и проста, как это кажется на первый взгляд. Пункт 2 ^[4] вводит используемые в данной статье обозначения, которые пригодятся в разделах 3 ^[5] и 4 ^[6], посвящённых выводу формул метода Уэлфорда для, соответственно, вычисления взвешенных средних и взвешенных ковариаций. Если вам неинтересны технические подробности вывода формул, вы можете пропустить эти разделы. Пункт 5 ^[7] содержит результаты экспериментального сравнения методов, а в заключении ^[8] находится пример реализации алгоритмов на языке С++.

Модельный код для сравнения методов вычисления ковариации находится в моём проекте на github ^[10]. Более сложный код, в котором метод Уэлфорда применяется для решения задачи линейной регрессии, находится в другом проекте ^[11], речь о котором пойдёт в следующих статьях.

1. Погрешности при вычислении средних

Начну c классического примера. Пусть есть простой класс, вычисляющий среднее для набора чисел:

class TDummyMeanCalculator {
private:
    float SumValues = 0.;
    size_t CountValues = 0;
public:
    void Add(const float value) {
        ++CountValues;
        SumValues += value;
    }
    double Mean() const {
        return CountValues ? SumValues / CountValues : 0.;
    }
};

Попробуем применить его на практике следующим способом:

int main() {
    size_t n;
    while (std::cin >> n) {
        TDummyMeanCalculator meanCalculator;
        for (size_t i = 0; i < n; ++i) {
            meanCalculator.Add(1e-3);
        }
        std::cout << meanCalculator.Mean() << std::endl;
    }
    return 0;
}

Что же выведет программа?

Ввод	Вывод
10000	0.001000040
1000000	0.000991142
100000000	0.000327680
200000000	0.000163840
300000000	0.000109227

Начиная с некоторого момента, сумма перестаёт меняться после прибавления очередного слагаемого: это происходит, когда SumValues оказывается равным 32768, т.к. для представления результата суммирования типу float просто не хватает разрядности.

Из этой ситуации есть несколько выходов:

1. Перейти с float на double.
2. Использовать один из более сложных методов суммирования ^[12].
3. Использовать метод Кэхэна ^[13] для суммирования.
4. Наконец, можно использовать метод Уэлфорда ^[14] для непосредственного вычисления среднего.

Не так просто найти данные, на которых плохо работает решение с использованием double. Тем не менее, такие данные встречаются, особенно в более сложных задачах. Также неприятно, что использование double увеличивает затраты памяти: иногда требуется хранить большое количество средних одновременно.

Методы Кэхэна и другие сложные способы суммирования по-своему хороши, но в дальнейшем мы увидим, что метод Уэлфорда всё же работает лучше, и, кроме того, он удивительно прост в реализации. Действительно, давайте посмотрим на соответствующий код:

class TWelfordMeanCalculator {
private:
    float MeanValues = 0.;
    size_t CountValues = 0;
public:
    void Add(const float value) {
        ++CountValues;
        MeanValues += (value - MeanValues) / CountValues;
    }

    double Mean() const {
        return MeanValues;
    }
};

К вопросу о корректности этого кода мы вернёмся в дальнейшем. Пока же заметим, что реализация выглядит достаточно простой, а на тех данных, что используются в нашей программе, еще и работает с идеальной точностью. Это происходит из-за того, что разность value - MeanValues на первой итерации в точности равна среднему, а на последующих итерациях равна нулю.

Этот пример иллюстрирует основное достоинство метода Уэлфорда: все участвующие в арифметических операциях величины оказываются "сравнимы" по величине, что, как известно, способствует хорошей точности вычислений.

Ввод	Вывод
10000	0.001
1000000	0.001
100000000	0.001
200000000	0.001
300000000	0.001

В этой статье мы рассмотрим применение метода Уэлфорда к ещё одной задаче — задаче вычисления ковариации. Кроме того, мы проведём сравнение различных алгоритмов и получим математические доказательства корректности метода.

2. Обозначения

Вывод формулы часто можно сделать очень простым и понятным, если выбрать правильные обозначения. Попробуем и мы. Будем считать, что заданы две последовательности вещественных чисел: и , и последовательность соответствующих им весов :

Поскольку мы хотим вычислять средние и ковариации, нам понадобятся обозначения для взвешенных сумм и сумм произведений. Попытаемся описать их единообразно:

Тогда, например, — это сумма весов первых элементов, — это взвешенная сумма первых чисел первой последовательности, а — сумма взвешенных произведений:

Также понадобятся средние взвешенные величины:

Наконец, введём обозначения для ненормированных "разбросов" и нормированных ковариаций :

3. Вычисление средних

Докажем взвешенный аналог формулы, использованной нами выше для вычисления среднего по методу Уэлфорда. Рассмотрим разность :

В частности, если все веса равняются единице, получим, что

Кстати, формулы для "взвешенного" случая позволяют легко реализовывать операции, отличные от добавления ровно одного очередного числа. Например, удаление числа из множества, по которому вычисляется среднее — это то же, что добавление числа с весом . Добавление сразу нескольких чисел — то же, что добавление одного из среднего с весом, равным количеству этих чисел, и так далее.

4. Вычисление ковариаций

Покажем, что и для взвешенной задачи верна классическая формула для вычисления ковариации. Сейчас для простоты будем работать с ненормированными величинами.

Отсюда уже легко видеть, что

Эта формула чрезвычайно удобна, в том числе и для онлайн-алгоритма, однако, если величины и окажутся близкими и при этом большими по абсолютному значению, её использование приведёт к существенным вычислительным погрешностям.

Давайте попробуем вывести рекуррентную формулу для , в каком-то смысле аналогичную формуле Уэлфорда для средних. Итак:

Рассмотрим последнее слагаемое:

Подставим получившееся в выражение для :

Код, реализующий вычисления по этой формуле, при отсутствии весов выглядит очень просто. Необходимо обновлять две средних величины, а также сумму произведений:

double WelfordCovariation(const std::vector<double>& x, const std::vector<double>& y) {
    double sumProducts = 0.;
    double xMean = 0.;
    double yMean = 0.;

    for (size_t i = 0; i < x.size(); ++i) {
        xMean += (x[i] - xMean) / (i + 1);
        sumProducts += (x[i] - xMean) * (y[i] - yMean);
        yMean += (y[i] - yMean) / (i + 1);
    }

    return sumProducts / x.size();
}

Также интересным является вопрос об обновлении величины собственно ковариации, т.е. нормированной величины:

Рассмотрим первое слагаемое:

Вернёмся теперь к рассмотрению :

Это можно переписать, например, так:

Получилась формула, действительно обладающая удивительным сходством с формулой для обновления среднего!

5. Экспериментальное сравнение методов

Я написал небольшую программу ^[10], в которой реализуются три способа вычисления ковариации:

1. "Стандартный" алгоритм, напрямую вычисляющий величины , и .
2. Алгоритм, использующий метод Кэхэна.
3. Алгоритм, использующий метод Уэлфорда.

Данные в задаче формируются следующим образом: выбираются два числа, и — средние двух выборок. Затем выбираются еще два числа, и — соответственно, отклонения. На вход алгоритмам подаются последовательности чисел вида

причём знаки при отклонениях меняются на каждой итерации, так, чтобы истинная ковариация вычислялась следующим образом:

Истинная ковариация константна и не зависит от числа слагаемых, поэтому мы можем вычислять относительную погрешность вычисления для каждого метода на каждой итерации. Так, в текущей реализации , а средние принимают значения 100000 и 1000000.

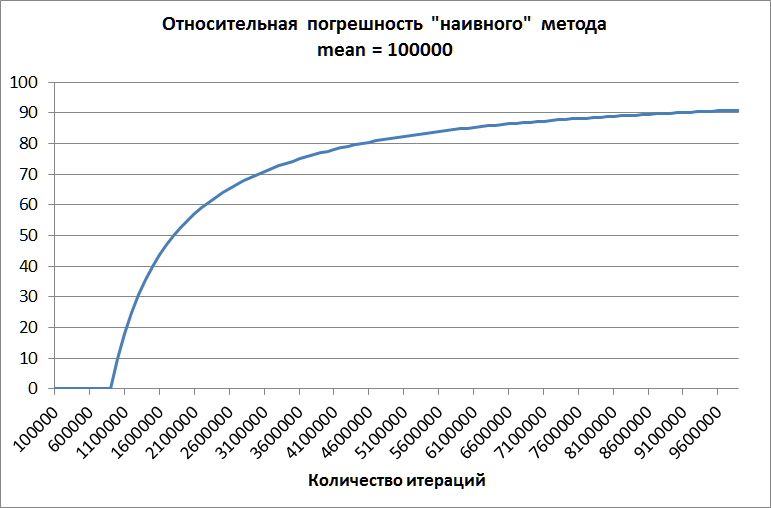
На первом графике изображена зависимость величины относительной погрешности при использовании наивного метода для среднего, равного 100 тысячам. Этот график демонстрирует несостоятельность наивного метода: начиная с какого-то момента погрешность начинает быстро расти, достигая совершенно неприемлемых величин. На тех же данных методы Кэхэна и Уэлфорда не допускают существенных ошибок.

Второй график построен для метода Кэхэна при среднем, равном одному миллиону. Ошибка не растёт с увеличением количества слагаемых, но, хотя она и существенно ниже, чем ошибка "наивного" метода, всё равно она слишком велика для практических применений.

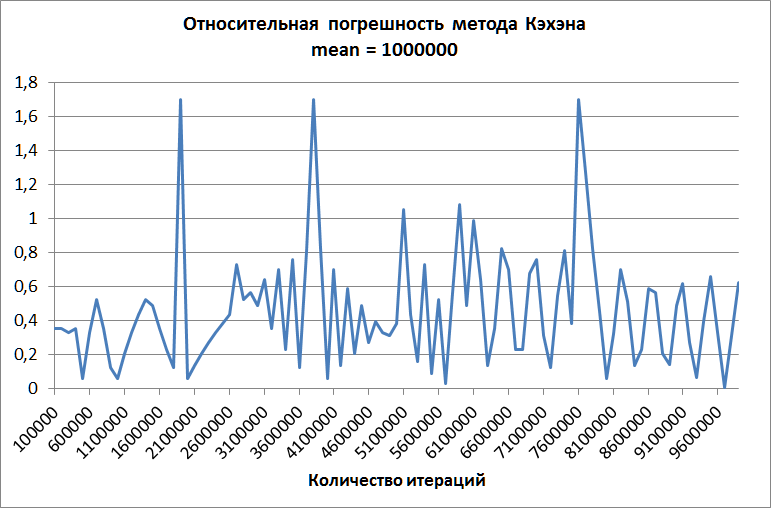
Метод Уэлфорда, в свою очередь, и на этих данных демонстрирует идеальную точность!

Заключение

В этой статье мы сравнили несколько способов вычисления ковариации и убедились в том, что метод Уэлфорда даёт наилучшие результаты. Для того, чтобы использовать его на практике, достаточно запомнить лишь две следующие реализации:

class TWelfordMeanCalculator {
private:
    double Mean = 0.;
    size_t Count = 0;
public:
    void Add(const float value) {
        ++Count;
        Mean += (value - Mean) / Count;
    }
    double GetMean() const {
        return Mean;
    }
};

class TWelfordCovariationCalculator {
private:
    size_t Count = 0;
    double MeanX = 0.;
    double MeanY = 0.;
    double SumProducts = 0.;
public:
    void Add(const double x, const double y) {
        ++Count;
        MeanX += (x - MeanX) / Count;
        SumProducts += (x - MeanX) * (y - MeanY);
        MeanY += (y - MeanY) / Count;
    }
    double Covariation() const {
        return SumProducts / Count;
    }
};

Использование этих методов может сэкономить много времени и сил в ситуациях, когда данные устроены достаточно "неудачно". Натолкнуться на проблемы с точностью вычислений можно в сколь угодно неожиданных ситуациях, даже при реализации одномерного алгоритма kMeans.

В следующей статье мы рассмотрим применение рассмотренных методов в задаче восстановления линейной регрессии, поговорим о скорости вычислений и о том, как справляются с "плохими" данными распространённые реализации методов машинного обучения.

Литература

1. github.com: Different covariation calculation methods ^[10]
2. machinelearning.ru: Сложение большого множества чисел, существенно отличающихся по величине ^[12]
3. ru.wikipedia.org: Алгоритм Кэхэна ^[13]
4. en.wikipedia.org: Algorithms for calculating variance: Online algorithm ^[14]

Автор: ashagraev

Источник ^[1]