Naive Spellchecking, или поиск ближайших слов из словаря по метрике Левенштейна на Scala

Приветствую! В этой статье будет показан алгоритм поиска ближайших к заданному слов из корпуса в терминах метрики Левенштейна. Наивным spellchecking-ом назван потому, что не учитывает ни морфологии, ни контекста, ни вероятности появления скорректированного слова в предложении, однако в качестве первого приближения сойдет вполне. Также алгоритм может быть расширен на поиск ближайших последовательностей из любых других сравнимых объектов, нежели простой алфавит из Char-ов, и, после допиливания напильником, его можно приспособить и для учета вероятностей появления скорректированных слов. Но в данной статье сосредоточимся на базовом алгоритме для слов определенного алфавита, скажем, английского.

Код в статье будет на Scala.

Всех заинтересовавшихся прошу под кат.

Intro

Вообще говоря, для поиска в метрическом пространстве существуют специализированные структуры данных, такие как VP-Tree (Vantage Point Tree). Однако эксперименты показывают, что для пространства слов с метрикой Левенштейна VP-дерево работает крайне плохо. Причина банальна — данное метрическое пространство очень плотное. У слова из, скажем, 4х букв, имеется огромное множество соседей на расстоянии 1. На больших расстояниях количество вариантов становится сопоставимо с размером всего множества, что делает поиск в VP-дереве ничуть не более производительным, чем линейный поиск по множеству. К счастью, для строк существует более оптимальное решение, и сейчас мы его разберем.

Описание

Для компактного хранения множества слов с общим префиксом используем такую структуру данных, как бор (trie).

Картинка бора из Википедии

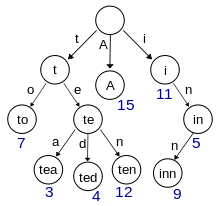
В двух словах алгоритм описывается как простой поиск алгоритмом Дейкстры на неявном графе вариантов префиксного совпадения искомого слова и слов в боре (trie). Узлами графа при нечетком поиске будут являться вышеназванные варианты, а весами ребер — собственно расстояние Левенштейна заданного префикса строки и узла бора.

Базовая реализация бора

Для начала, опишем узел бора, напишем алгоритм вставки и четкого поиска слова в боре. Нечеткий поиск оставим на закуску.

class Trie(
  val ends: Boolean = false, // whether this node is end of some string
  private val parent: Trie = null,
  private val childs : TreeMap[Char, Trie] = null,
  val value : Char = 0x0)

Как видим, ничего сверхъестественного. Узел бора представляет собой объект со ссылкой на родителя, Map-ой ссылок на потомков, буквенным значением узла, и флагом, является ли узел конечным узлом для какой-нибудь строки.

Теперь опишем четкий поиск в боре:

/// exact search
def contains(s: String) = {
  @tailrec def impl(t: Trie, pos: Int): Boolean =
    if (s.size < pos) false
    else if (s.size == pos) t.ends
    else if (t.childs == null) false
    else if (t.childs.contains(s(pos)) == false) false
    else impl(t.childs(s(pos)), pos + 1)

  impl(this, 0)
}

Ничего сложного. Спускаемся по детям узла до тех пор, пока не встретим совпадение (t.ends) или не увидим, что дальше спускаться некуда.

Теперь — вставка:

/// insertion
def +(s: String) = {
  def insert(trie: Trie, pos: Int = 0) : Trie = 
    if (s.size < pos) trie
    else if (pos == 0 && trie.contains(s)) trie
    else if (s.size == pos)
      if (trie.ends) trie
      else new Trie(true, trie.parent, trie.childs, trie.value)
    else {
      val c = s(pos)
      val children = Option(trie.childs).getOrElse(TreeMap.empty[Char, Trie])
      val child = children.getOrElse(
          c, new Trie(s.size == pos + 1, trie, null, c))
      new Trie(
        trie.ends, 
        trie.parent, 
        children + (c, insert(child, pos + 1)), 
        trie.value)
  }

  insert(this, 0)
}

Наш бор — immutable, так что функция + возвращает нам новый бор.

Построение бора из корпуса слов выглядит как-то так:

object Trie {
  def apply(seq: Iterator[String]) : Trie = 
    seq.filter(_.nonEmpty).foldLeft(new Trie)(_ + _)

  def apply(seq: Seq[String]) : Trie = apply(seq.iterator)
}

Базовое построение готово.

Нечеткий поиск, базовая функция

Опишем узел графа:

case class Variant(val pos: Int, val node: Trie)(val penalty: Int)

Pos — позиция, на которой заканчивается префикс искомой строки в рассматриваемом варианте. Node — префикс бора в рассматриваемом варианте. Penalty — расстояние Левенштейна префикса строки и префикса бора.

Каррированный case-class означает, что функции equals/hashCode компилятор будет генерить только для первого argument-list'а. Penalty в сравнении Variant-ов не учитываются.

Перебором узлов графа с неубывающим penalty заведует функция с вот такой сигнатурой:

def prefixes(toFind: String): Stream[Variant]

Для ее реализации напишем небольшой хелпер, генерирующий Stream функцией-генератором:

 def streamGen[Ctx, A]
    (init: Ctx)(gen: Ctx => Option[(A, Ctx)]): Stream[A] =
  {
    val op = gen(init)
    if (op.isEmpty) Stream.Empty
    else op.get._1 #:: streamGen(op.get._2)(gen)
  }

Теперь реализуем immutable context поиска, который мы будем передавать в функцию выше, и который содержит в себе все, что нужно для перебора узлов неявного графа алгоритмом Дейкстры: очередь с приоритетом и множество посещенных узлов:

 private class Context(
    // immutable priority queue, Map of (penalty-, prefix pos+) -> List[Variant]
    val q: TreeMap[(Int, Int), List[Variant]],
    
    // immutable visited nodes cache
    val cache: HashSet[Variant])                 
  {
    // extract from 'q' value with lowest penalty and greatest prefix position
    def pop: (Option[Variant], Context) = {
      if (q.isEmpty) (None, this)
      else {
        val (key, list) = q.head
        if (list.tail.nonEmpty)
          (Some(list.head), new Context(q - key + (key, list.tail), cache))
        else
          (Some(list.head), new Context(q - key, cache))
      }
    }

    // enqueue nodes
    def ++(vars: Seq[Variant]) = {
      val newq = vars.filterNot(cache.contains).foldLeft(q) { (q, v) =>
        val key = (v.penalty, v.pos)
        if (q.contains(key)) { val l = q(key); q - key + (key, v :: l) }
        else q + (key, v :: Nil)
      }
      new Context(newq, cache)
    }

    // searches node in cache
    def apply(v: Variant) = cache(v)

    // adds node to cache; it marks it as visited
    def addCache(v: Variant) = new Context(q, cache + v)
  }

  private object Context {
    def apply(init: Variant) = {
      // ordering of prefix queue: min by penalty, max by prefix pos
      val ordering = new Ordering[(Int, Int)] {
        def compare(v1: (Int, Int), v2: (Int, Int)) =
          if (v1._1 == v2._1) v2._2 - v1._2 else v1._1 - v2._1
      }

      new Context(
        TreeMap(((init.penalty, init.pos), init :: Nil))(ordering),
        HashSet.empty[Variant])
    }
  }

Очередь узлов сделана из простой immutable TreeMap-ы. Ноды в очереди сортированы по возрастанию penalty и убыванию prefix pos.

Ну и наконец сам генератор стрима вариантов:

  // impresize search lookup, returns stream of prefix match variants with lowest penalty
  def prefixes(toFind: String) : Stream[Variant] = {
    val init = Variant(0, this)(0)

     // returns first unvisited node
    @tailrec def whileCached(ctx: Context): (Option[Variant], Context) =
    {
      val (v, ctx2) = ctx.pop
      if (v.isEmpty) (v, ctx2)
      else if (!ctx2(v.get)) (Some(v.get), ctx2)
      else whileCached(ctx2)
    }

    // generates graph edges from current node
    def genvars(v: Variant): List[Variant] = {
      val replacePass: List[Variant] = 
        if (v.node.childs == null) Nil
        else v.node.childs.toList flatMap { pair =>
          val (key, child) = pair
          val pass = Variant(v.pos, child)(v.penalty + 1) :: Nil
          if (v.pos < toFind.length)
            Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1}) :: pass
          else pass
        }

      if (v.pos != toFind.length) {
        Variant(v.pos + 1, v.node)(v.penalty + 1) :: replacePass
      } else replacePass
    }

    streamGen(Context(init)) { ctx =>
        val (best, ctx2) = whileCached(ctx)
        best.map { v =>
          (v, (ctx2 ++ genvars(v)).addCache(v))
        }
      }
  }

Наибольшего внимания тут заслуживает, разумеется, genvars. Она для данного узла графа генерирует ребра, исходящие из него. Для каждого потомка узла бора данного варианта поиска мы генерируем вариант со вставкой символа

val pass = Variant(v.pos, child)(v.penalty + 1)

и заменой символа

Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1})

Если не дошли до конца строки — то генерим еще и вариант с удалением символа

Variant(v.pos + 1, v.node)(v.penalty + 1)

Нечеткий поиск, юзабилити

Конечно, функция prefixes для общего использования малопригодна. Напишем обертки, позволяющие нам искать более-менее осмысленно. Для начала, ограничим перебор вариантов некоторым разумным значением penalty для предотвращения застревания алгоритма на каком-нибудь слове, для которого в словаре не существует более-менее адекватной замены

def limitedPrefixes(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = {
  prefixes(toFind).takeWhile(_.penalty < penaltyLimit)
}

Далее отфильтруем варианты с полным, а не префиксным совпадением, то есть такие, у которых pos равен длине искомой строки, и node указывает на конечный узел с флагом ends == true:

def matches(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = {
  limitedPrefixes(toFind, penaltyLimit).filter { v => v.node.ends && v.pos == toFind.size }
}

Ну и наконец преобразуем стрим вариантов в стрим слов, для этого в классе Trie напишем код, который возвращает нам найденное слово:

def makeString() : String = {
    @tailrec def helper(t: Trie, sb: StringBuilder): String =
      if (t == null || t.parent == null) sb.result.reverse
      else {
	helper(t.parent, sb += t.value)
      }

    helper(this, new StringBuilder)
  }

Ничего сложного. Поднимаемся по parent-ам, записывая значения узлов, пока не встретим корень бора.

Ну и наконец:

def matchValues(toFind: String, penaltyLimit: Int = 5): Stream[String] = {
  matches(toFind, penaltyLimit).map(_.node.makeString)
}

Итого

Надо сказать, что функция matches весьма универсальна. Используя ее, можно производить поиск K ближайших, делая просто

matches(toFind).take(k).map(_.node.makeString)

или поиск Delta-ближайших, то есть строк на расстоянии не больше D:

matches(toFind).takeWhile(_.penalty < d).map(_.node.makeString)

Еще алгоритм можно расширить, вводя разные веса для вставки/удаления/замены символов. В класс Variant можно добавить конкретные счетчики замен/удалений/вставок. Trie можно обобщить, чтобы можно было в конечных узлах хранить значения, и в качестве ключей использовать не только строки, но и индексированные последовательности любых сравнимых типов ключей. Также можно каждый узел бора помечать вероятностью его встретить (для конечного узла это вероятность встретить слово + вероятности встретить все слова-потомки, для промежуточного — только сумма вероятностей потомков) и учитывать этот вес при расчете penalty, но это все находится уже за рамками данной статьи.

Надеюсь, было интересно. Код тут

Автор: Ilya

Источник