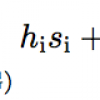
В компании Intel разрабатывается довольно много ПО для моделирования различных физических процессов. В некоторых из них мы используем пакет OpenFOAM, и в этом посте я постараюсь дать краткое описание его возможностей.
Что такое OpenFOAM? Это, пользуясь термином Википедии, открытая (GPL) платформа для численнного моделирования — в первую очередь для моделирования, связанного с решением уравнений в частных производных методом конечных объемов, и в самую первую очередь — для решения задач механики сплошных сред.
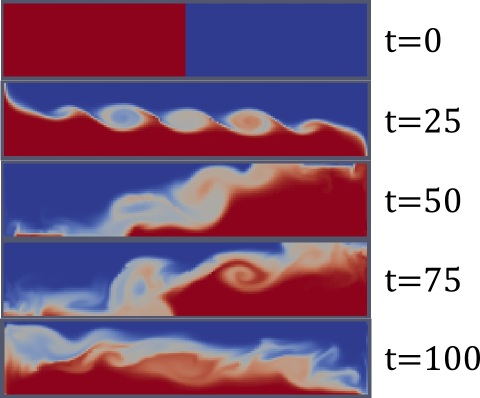
КПДВ: эволюция двух несмешивающихся жидкостей разной плотности, изначально разделенных тонкой перегородкой (пример «lockExchange» из стандартной поставки OpenFOAM). Переходные цвета обозначают ячейки сетки, где присутствует доля и той, и другой жидкости (более точно: при симуляции используется метод объёма жидкости).
Реально OpenFOAM, фактически, состоит из двух частей: это, во-первых, библиотека классов для многих операций, необходимых при численном моделировании, — и во-вторых, библиотека программ («солверов»), использующих эти классы и позволяющих решать конкретные задачи моделирования. Соответственно, и пост мой будет состоять из двух разделов: в первом я (вкратце) опишу библиотеку программ и расскажу об использовании OpenFOAM с позиции человека, который не хочет лезть в непосредственно программный код; во втором я постараюсь слегка подробнее остановиться на программировании под OpenFOAM.
Использование OpenFOAM
Я не буду подробно останавливаться на пошаговых инструкциях по подготовке данных для OpenFOAM и непосредственно по его запуску. Простейший пример описан в официальном руководстве и дает довольно хорошее представление о том, как работать с практически любым OpenFOAM-солвером. Скажу только, что для запуска OpenFOAM вам надо подготовить целый каталог с определенной структурой файлов, в которых разместить различные параметры задачи (описание сетки, длительность моделирования, параметры для выбора шага по времени и т.д.), физические свойства исследуемой системы (вязкости/теплоемкости жидкостей или т.п.) и начальные/граничные условия. Конкретная структура каталогов и файлов, конечно, определяется конкретной программой-солвером, но общая схема почти всегда одинакова. В частности, все файлы, содержащие разные данные, записываются в особом иерархическом формате «словарей», имеющих довольно простую структуру; примеры есть по ссылке выше.
После подготовки структуры файлов надо запустить солвер. Все стандартные OpenFOAM-солверы — консольные приложения с минимальным взаимодействием с пользователем. В итоге, если все будет хорошо, в рабочем каталоге будет создано несколько новых подкаталогов, в которые будут записаны результаты вычислений в указанные промежуточные моменты времени. Эти файлы можно преобразовывать в различные форматы (например, в популярный VTK), для этого в OpenFOAM предусмотрено множество конверторов, — а можно и непосредственно просматривать, например, в ParaView.
Перечислю также некоторых из нескольких стандартных OpenFOAM-солверов. В OpenFOAM входят программы для:
• решения «простых» задач движения сжимаемых и несжимаемых жидкостей с поддержкой разных термодинамических моделей и разных моделей турбулентности;
• решения задач движения жидкостей/газов с учетом химических процессов;
• решения задач магнитной гидродинамики;
• и многого другого, вплоть до даже финансовой модели Блэка—Шоулза.
Полный список стандартных солверов с кратким их описанием есть на сайте OpenFOAM. Правда, к сожалению, многие из них документированы довольно плохо, и, чтобы понять, какие конкретно уравнения они решают и каких параметров требуют, приходится лезть в код. Вообще, это относится ко многим аспектам OpenFOAM — многие возможности или вообще не документированы, или документированы весьма плохо, и о них можно узнать либо из кода, либо из примеров.
Программирование под OpenFOAM
Базовые классы
Как же выглядит OpenFOAM с точки зрения программиста? Ну, во-первых, конечно, здесь есть набор многих элементарных классов и поддержка элементарных операций, которые стоит ожидать от любого физического кода. Векторы, тензоры; скалярное, векторное, тензорное произведения; след тензора и т.д. Правда, к сожалению, все только трехмерное, и с тензорами выше второго, если не ошибаюсь, ранга плохо.
Далее, конечно, класс сетки (точнее, целая иерархия классов, хранящих разные данные сетки — чисто геометрические координаты; информацию, необходимую для работы с разреженными матрицами; информацию, необходимую для метода конечных объемов; и т.д.). Класс (а точнее, опять иерархия классов) для физических полей, определенных на сетке. Иерархия классов для граничных условий — все граничные условия задаются классами со стандартным интерфейсом, что позволяет выбирать нужное гранусловие на этапе запуска солвера, а вовсе не в процессе его написания.
Естественно, для всех этих классов переопределены операторы сложения/умножения и т.д., сложение двух полей или вычисление (поточечное) функции Бесселя от поля делается в одну строчку.
Дифференцирование
Собственно, уже эти классы позволяют существенно проще писать код, выполняющий численное моделирование. Но на самом деле жемчужина OpenFOAM, возможность, без которой не обходится ни один его обзор, — это пространства имен fvc и fvm. В них определены такие функции как grad, div, curl, laplacian и т.д. для вычисления различных пространственных производных (соответственно, градиента, дивергенции, ротора, лапласиана и т.д.), а также ddt и d2dt2 для производных по времени. В результате, если у вас есть какое-то поле psi, то его градиент вычисляется простым вызовом fvc::grad(psi), и т.п.
На самом деле fvc::grad и т.п. — это «внешний интерфейс» для ряда разных функций, вычисляющих градиент по разным схемам; выбор конкретной схемы выполняется на этапе выполнения программы в соответствии с тем, что написано в файлах параметров задачи. Соответственно, есть возможность, не меняя кода солвера, изменять используемые для численного дифференцирования схемы.
Таким образом, если мне надо вычислить поле 
, я так и пишу в коде:
fvc::div(U) + alpha * fvc::laplacian(phi)
Обратите внимание, что, во-первых, в этом коде нигде не фигурируют никакие параметры сетки — функции типа div сами их узнают (за счет того, что каждое поле хранит ссылку на свою сетку) и правильно учтут. Во-вторых, аналогично, здесь не фигурируют явно гранусловия — но они так же будут корректно учтены.
OpenFOAM может работать с сетками произвольной структуры (ну собственно на то он и метод конечных объемов), но даже если бы в стандартном коде и были бы ограничения по структуре сетки, от них можно было бы избавиться переписыванием функций типа grad, не исправляя код солверов.
fvm:: и решение уравнений
Но, чтобы решать уравнения, недостаточно просто уметь вычислять выражения с пространственными производными. Рассмотрим для начала достаточно простой случай: уравнение (классическое для обзоров по OpenFOAM)
Мы хотим его решать последовательными шагами по времени, вычисляя значения для каждого очередного момента времени по значениям переменных на предыдущем моменте времени. (Скорее всего, у нас будут еще уравнения в системе, но с ними все делается аналогично.)
Независимо от способов дискретизации производных, искать «новые» значения можно, как известно, «явным» и «неявным» методом. В первом случае мы просто вычисляем, исходя из «текущих» значений , все пространственные производные, из них получаем производную — и в соответствие с ней находим «новое» значение . Во втором случае мы ищем такие «новые» значения , чтобы при их подстановке в уравнение во все места вхождения оно выполнялось — т.е. мы получаем (в данном случае линейную, см. на этот счет ниже) систему уравнений на «новое» значение , которую и решаем.
В общем-то, понятно, что оба случая можно представить в виде уравнения , где — некоторая матрица, а — некоторое поле. В первом случае матрица будет диагональной (имея вид ), а поле будет содержать член и полностью все вычисленные значения пространственных производных. А во втором случае матрица будет содержать еще и недиагональные элементы, определяемые пространственными производными, а, соответственно, поле будет содержать меньше составляющих.
Именно для различия этих двух подходов и есть пространства имен fvc и fvm. А именно, функции пространства имен fvc возвращают соответствующее поле — т.е. как раз то, что нужно для явного метода; а функции fvm возвращают особый объект, хранящий вклад от соответствующего члена в матрицу и в поле .
Соответственно, на OpenFOAM явный способ выглядит так:
solve
(
fvm::ddt(rho,U)
+ fvc::div(phi,U)
- fvc::laplacian(mu,U)
==
- fvc::grad(p)
);
а неявный так:
solve
(
fvm::ddt(rho,U)
+ fvm::div(phi,U)
- fvm::laplacian(mu,U)
==
- fvc::grad(p)
);
И все. Очень красиво и удобно читать. Ну и легко явное представление каждого члена поменять на неявное и обратно.
(Оба этих кода делают только один шаг по времени, т.е. вычисляют новые значения по текущим значениям всех полей. Чтобы получить полноценный код моделирования, надо этот вызов solve — вместе с аналогичными вызовами для других решаемых уравнений — заключить во внешний цикл по времени.)
Три примечания. Во-первых, про то, почему функции дифференцирования иногда принимают два аргумента. На этот счет есть отдельные тонкости, связанные как с формой соответствующего члена (например, laplacian(mu, psi) соответствует , и аналогично для векторных полей), так и с тем, что поля, на самом деле, бывают заданы как в центрах ячеек сетки, так и на гранях сетки.
Во-вторых, конечно, все так красиво только пока уравнение линейное. Но понятно, что нелинейность явным способом учитывается легко, а вот если мы хотим ее учесть как-нибудь неявно, то придется что-то придумывать вручную, и общего разумного метода тут нет.
В-третьих, естественно, аналогичные подходы можно применять и для других уравнений и задач. Например, простое уравнение решается одним вызовом solve:
solve( fvm::laplacian(psi) + k*k*fvm::Sp(1, psi) = f );
— причем (поскольку уравнение линейное и не эволюционное) вы сразу получаете полностью искомое поле .
(Здесь fvm::Sp — функция, вводящая в уравнение непосредственно искомую функцию неявным образом без каких-либо производных. Если бы я написал просто psi, то получил бы ее явный учет, т.е. просто подстановку ее «текущих» значений.)
Размерности
Еще одна очень удобная возможность OpenFOAM — это встроенная поддержка размерности. Все поля, все численные параметры задачи хранят свою размерность. (Точнее, возможно докопаться до таких глубин кода, где размерность пропадает; но даже и там как правило можно добавить проверку размерности.) Поэтому в OpenFOAM надо очень постараться, чтобы сложить метры с килограммами.
На первый взгляд это кажется как минимум не очень нужной функциональностью — а порой даже откровенно мешающей; например, когда я только начинал писать простые солверы на OpenFOAM для уравнений типа приведенного выше , меня очень раздражала необходимость выставлять правильные размерности для и .
Но как только выражения становятся чуть более сложными, контроль размерностей реально помогает, устраняя проблемы и ошибки типа «вот эта — это энергия суммарная в ячейке? Или локальная энергия на единицу массы вещества? Или на один моль? Или на одну молекулу? А вот тут я вычисляю силу со стороны электрического поля и подставляю в уравнение — мне надо ее умножать на плотность или нет?»
Правда, все не так радужно — местами есть куски кода, где никакого контроля размерностей не производится, а местами приходится и самому такой код писать (особенно если надо делать настолько нетривиальные операции над полями, что приходится таки писать цикл по всем ячейкам, а не пользоваться перегруженными операторами для полей). В одном месте вообще в большом куске кода потеряна размерность «моль», т.е. все вычисления реально ведутся в молях, но в размерностях это нигде не фигурирует. Но даже то, что есть — очень удобно.
Модели для расчетов механики сплошных сред
Фактически, все, что обсуждалось выше, не имеет непосредственного отношения к механике сплошных сред, а относится только к методу конечных объемов. Это позволяет считать OpenFOAM не просто платформой для расчетов МСС, но вообще платформой для расчетов методом конечных элементов — и действительно, есть примеры применения OpenFOAM для моделирования, не связанного с МСС.
Но тем не менее, помимо классов для метода конечных объемов, огромная часть кода OpenFOAM относится именно к задачам механики сплошных сред. Это — уже вкратце упоминавшиеся модели термодинамических свойств веществ, реализующие, к примеру, модель постоянной теплоемкости или рассчитывающие теплоемкости по таблицам JANAF. Это различные модели турбулентности. Это целая иерархия классов для химических расчетов. Это модели поверхностных пленок и т.д.
Причем все эти модели как правило реализованы в полноценных традициях объектно-ориентированного программирования: все классы для разных моделей одного физического процесса имеют общий интерфейс, и код, использующий эти классы, не должен знать о том, какая именно модель используется. Более того, выбор конкретной модели определяется на этапе выполнения — пользователь может сам в файле настроек выбрать нужную модель.
Эти возможности динамического выбора моделей относятся не только к МСС-моделям, но и к основному коду метода конечных объемов. Например, как уже упоминалось, конкретные схемы вычисления градиента, или конкретные типы граничных условий тоже выбираются на этапе выполнения.
Цепочки шаблонов
Код OpenFOAM очень широко использует шаблоны. При этом очень активно используется следующая интересная структура (если кто-нибудь подскажет, как она называется, я буду благодарен). Есть, допустим, некоторый базовый класс. И есть целое множество шаблонных классов, наследующих свой параметр:
template <class T> class Foo: public T
при этом каждый такой класс добавляет к своему предку какие-либо новые свойства/особенности, а в итоге используется целая цепочка таких шаблонов типа Foo<Bar<Baz<Base> > >.
Например, простейший класс, хранящий термодинамические свойства вещества, имеет вид constTransport<specieThermo<hConstThermo<perfectGas> > >. Здесь perfectGas — класс, отвечающий (грубо) за вычисление плотности газа по давлению и температуре и т.п.; hConstThermo добавляет к классу хранение (постоянной) теплоемкости при фиксированном давлении и вычисление энтальпии по температуре и наоборот; specieThermo позволяет пересчитывать другие функции типа теплоемкости при фиксированном объеме или энтропии; а constTransport добавляет хранение (постоянных) вязкости и теплопроводности и предоставляет к ним доступ.
Для каждого такого «уровня» есть, как правило, несколько реализаций. Например, вместо constTransport можно использовать sutherlandTransport, вычисляющий вязкость и теплопроводность по температуре в соответствии с формулой Сазерленда. В результате можно сочетать разные модели для разных термодинамических свойств, тем самым порождая те комбинации, которые требуются. Аналогичные конструкции встречаются во всем коде OpenFOAM.
Другие программистские особенности
Еще хочется отметить несколько более технических деталей, скорее со знаком минус.
Во-первых, несмотря на то, что основная библиотека представляет из себя набор классов, допускающих простое повторное использование, все стандартные солверы написаны в простом процедурном стиле, а в большинстве случаев — весь код солвера состоит из одной функции main. А именно, например, солвер icoFoam реализует не самый тривиальный метод PISO. И в нем и собственно основной цикл моделирования, и весь внутренний цикл PISO реализованы в функции main, что существенно усложняет использование этого же кода в своем солвере.
Во-вторых, в коде солверов активно используется подключение .H-файлов не как заголовочных файлов, а просто как заранее заготовленных кусков кода. Например, почти во всех солверах функция main начинается так:
int main(int argc, char *argv[])
{
#include "setRootCase.H"
...
при этом файл setRootCase.H имеет следующее содержание (с точностью до комментариев):
Foam::argList args(argc, argv);
if (!args.checkRootCase())
{
Foam::FatalError.exit();
}
(и находится даже не в каталоге солвера, а в каталоге исходников библиотеки OpenFOAM — и все солверы используют один файл.)
В-третьих, в OpenFOAM нет поддержки комплексных чисел. Причем, когда они мне понадобились, я подумал, что все будет просто: все поля, все основные классы, все основные функции — шаблонные, и я думал, что достаточно написать Field<complex>. Но нет! Оказалось (и это в-четвертых), что поле-то шаблонные, а вот многие функции определены только для конкретной специализации шаблона.
Наконец, в-пятых, у OpenFOAM весьма нетривиальная и, насколько я понимаю, нестандартная, процедура сборки, установки и настройки. Она требует прописывания вручную в файле настроек пути, куда установлен OpenFOAM, требует (автоматизированного, правда) прописывания нескольких переменных окружения, использует свои скрипты для сборки (wmake) и т.д.
Заключение
Еще много чего хочется написать, привести какие-нибудь примеры и т.д. — но пост и так уже очень длинный. Поэтому просто еще раз отмечу, что использование OpenFOAM реально упрощает и ускоряет разработку программ для численного моделирования физических процессов, — а еще и резко снижает опасность ошибок.
Ссылки
- Официальный сайт OpenFOAM
- Официальная документация (User Guide)
- Doxygen-документация по исходному коду
- Programmer's guide (почему-то отсутствует напрямую на сайте, а присутствует только в репозитории исходного кода)
- OpenFOAM-extend — форк OpenFOAM, содержащий, видимо, много дополнений, но существенно хуже документированный.
- Форум по OpenFOAM на cfd-online.com — ценный источник информации по элементарным проблемам с OpenFOAM; правда, чуть только проблемы становятся сложными, найти на форуме ответы становится затруднительно.
- В интернете есть еще много сайтов разных конференций по OpenFOAM, на которых выставлены pdf-файлы презентаций; они тоже бывают весьма полезны.
Автор: pkalinin
