В части 2 мы закончили с определениями всех формальных терминов и символов, которые вы можете увидеть в вопросе на StackOverflow об алгоритме Хиндли-Милнера. Так что теперь мы готовы перевести, о чём же там спрашивается, а именно — правила вывода утверждений о выводе типов. Приступим!
Правила для выведения утверждений о выводе типов
[Var]
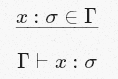
Это переводится так: если "x имеет тип σ" — положение из нашей коллекции положений Γ, то из Γ вы можете вывести, что x имеет тип σ. Здесь x — переменная (отсюда и название правила). Да, звучит оно до боли очевидно, однако содержит в себе глубокие и сложные факты в краткой и лаконичной форме, которую машина может понять. Это позволяет автоматизировать вывод типов.
[App]
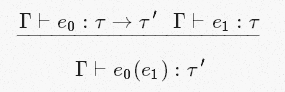
Это переводится так: если мы можем вывести, что e0 — это выражение с типом τ→τ′ (т.е. e0 может быть анонимной функцией, которая, в соответствии с Γ, принимает на вход значение типа τ и возвращает значение типа τ′), и что e1 имеет тип τ, тогда мы можем сделать вывод о том, что e0(e1) — выражение, полученное в результате применения e0к e1, имеет тип τ′. Интуитивно понятная суть: если мы можем вывести тип входа и выхода функции, а так же то, что некоторое выражение имеет тот же тип, что и вход, то когда мы применим функцию к этому выражению, мы можем смело делать вывод о том, что результирующее выражение будет иметь тип выхода функции. Ничего сбивающего с толку здесь нет.
[Abs]
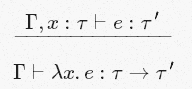
Это переводится так: если мы можем предположить, что x имеет тип τ, а e имеет тип τ′, то мы можем заключить, что также способны вывести тип абстракции/анонимизации e по отношению к переменной x — λx.e. Им будет являться τ→τ′. Т.е., например, если мы знаем, что тип x — String, то выражение x[0] будет иметь тип Char. Сейчас [Abs] позволяет нам заключить, что:
function(x) { return x[0]; }
имеет тип String→Char.
В сторону. Ранее я уже упоминал политипы. Давайте вернёмся к ним в этом примере, просто чтобы это понятие лучше уложилось в голове. Итак, вы уже заметили, что функция выше имеет тип Array[Int]→Int. Фактически, для любого типа t функция имеет тип Array[t]→t. Так что на самом деле она имеет множество различных типов, и String→Char — всего лишь один из них. Каждый из типов вида Array[t]→t является монотипом. Мы можем вывести, что данная функция обладает всеми этими монотипами, просто говоря, что она имеет политип ∀t(Array[t]→t). Читается: «для любых t — тип Array[t]→t», и мы обозначаем кучу всего единым типом (правда, более абстрактным). Итак, заметьте, что когда мы выводим тип какого-то выражения, то это не означает, что он является единственным для этого выражения. Оно может иметь множество различных типов, некоторые из которых будут более специализированными, а другие наоборот более абстрактными. Простейшие разновидности типов — это монотипы: Int, String, String→Char и тому подобное, но если мы захотим, то можем завести и более абстрактные/общие типы — политипы.
[Let]
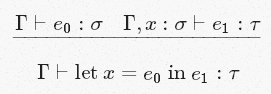
Вообще легко:
Если мы можем вывести, что e0 имеет тип σ
и
Если мы предполагаем, что x тоже имеет тип σ и из этого можем вывести, что e1 имеет тип τ
то
Мы можем заключить, что результат полагания x равным e0 и подстановки его в e1 будет иметь тип τ.
Последние четыре правила есть ни что иное, как формальное отображение наших интуитивных знаний о том, какой итоговый тип мы можем получить, если у нас есть переменные, с которыми мы создаём анонимные функции, или к которым применяем обычные функции, или подставляем выражения внутрь выражений. Это то, что мы, как программисты, делаем интуитивно. Здесь же мы просто говорим о том, как всё это описать формально. В конце-концов, не всё, что происходит в наших мозгах — неведомая магия. Стоит также отметить, что последние четыре правила в точности соответствуют четырём правилам, определяющим, что является допустимым выражением в лямбда-исчислении. И это не совпадение.
[Inst]
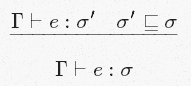
Это правило об экземплярах. Вы можете думать о монотипе Array[Int]→Int как об экземпляре политипа ∀t.Array[t]→t. Другими словами, это «специализация»: Array[Int]→Int более специализированный, чем ∀t.Array[t]→t. Мы обозначаем «более специализированный, чем» с помощью ⊑. Т.е.
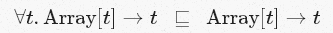
Таким образом, непосредственный перевод [Inst] таков: если мы можем вывести, что e имеет тип σ′, а σ является экземпляром/специализацией σ′, то мы можем заключить, что e имеет тип σ. Вы можете думать о σ и σ′ как об Array[t]→t и ∀t.Array[t]→t соответственно.
[Gen]
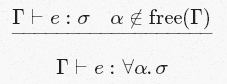
Это наиболее сложная часть для понимания. По-настоящему, только она имеет значение в контексте процесса вывода типов с использованием того узкого набора правил, который был изложен выше. У неё нет чёткого аналога, так как она во многом зависит от концепции переменной типа — чего-то, что никогда не встречается в реальных языках программирования, но является незаменимым, когда мы пытаемся работать с мета-языком, чтобы говорить о типах в любом произвольном языке программирования. В общих чертах идею можно показать на следующем «примере»:
Предположим, что у вас есть две переменные x и y, и в сначала вы предполагаете, что обе они имеют тип α, где α — переменная, обозначающая тип. Позже вам встречается выражение, для которого вы каким-то образом вывели, что его тип α→α в данном контексте (контексте предположения, что x и y имеют тип α). А теперь внимание — вопрос: будет ли эта функция иметь политип ∀α.α→α? Т.е. связывает ли эта функция в общем объекты с одинаковым типом, или так только кажется, потому что вы предположили, что x и y имеют одинаковый тип α?
Поскольку α — переменная типа, т.е. может обозначать любой тип, то мы хотели бы думать, что раз уж мы вывели, что e имеет тип α→α, то оно обладает и политипом ∀α.α→α. Но мы не можем сказать, что это обобщение является обязательным, без более полного понимания того, как e связано с x и y. В частности, если наш вывод о том, что оно имеет тип α→α, сильно завязан на наши предыдущие предположения, связанные с этим типом, то мы вообще не можем делать вывод, что e имеет политип ∀α.α→α.
А теперь (наконец-то!) перевод правила:
Если некоторая переменная типа α не «свободно» упоминается в нашем текущем контексте/наборе знаний/предположений, и мы можем вывести, что некое выражение e имеет какой-то тип σ, то мы можем заключить, что e имеет тип σ вне зависимости от того, чем в итоге обернётся α. Чуть более технически: e имеет политип ∀α.σ.
Ладно, но что означает «свободно упомянутый»? В политипе ∀α.α→α, α не упоминается «по-настоящему». Этот тип полностью аналогичен, например, ∀β.β→β. Выражение с любым из этих типов — обычная функция, которая имеет одинаковые типы входа и выхода. С другой стороны, x:α — «настоящее» упоминание α.
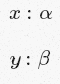
и
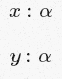
означают разные вещи. Последний говорит о том, что x и y определённо имеют одинаковый тип (даже если этот тип ещё не был определён). Первый же не сообщает о связи типов x и y ровным счётом ничего. Разница в том, что когда α упоминается внутри области ∀ (как в случае ∀α.α→α), то она — всего лишь фикция, которую можно заменить на любую другую переменную типа, независимо от оставшейся части контекста. Таким образом, мы можем интерпретировать положение “α несвободно упоминается в контексте Γ” как “α либо вообще не упомянуто, либо считается фикцией и в принципе может быть заменена на что-то совершенно другое без изменения семантики знаний/предположений в нашем контексте”.
Вот и всё.
Примечание переводчика: я буду очень признательна за любые замечания в личку по поводу перевода.
Автор: AveNat








