Недавно я решил написать программу, которая будет выдавать алгоритм решения некоторых механических головоломок, таких как кубик 2х2х2, 3х3х1, пирамидка и других. Полный список есть в интерфейсе программы, а также на её сайте, но об этом позже. Естественно, алгоритм этот должен быть самым коротким, иначе не интересно: можно было бы забить туда известные формулы, чтобы она собирала как человек. Сразу скажу две причины, почему я не стал включать в список кубик Рубика 3х3: во-первых, из за его популярности. Наверняка есть уже куча софта для этого, не хочется изобретать велосипед. Ну и во-вторых, из за его сложности: начав писать программу, я хотел «потренироваться» на чём-нибудь попроще. Итак, приступим.
Для начала, рассмотрим всё на примере головоломки под названием floppy cube, которая по форме является параллелепипедом 3x3x1:

Это самая простая вещь, которая есть в моей коллекции. Что же с ней можно делать? Можно повернуть правую сторону из трёх кусочков на 180 градусов, будем обозначать это движение как R. С таким же успехом можно повернуть левую сторону (L), переднюю (F) и заднюю (B).
Всего на головоломке 30 наклеек. Цвета этих наклеек будем хранить в массиве s[0..29]; действия R,L,B,F оформим в виде функций, которые каким-то образом меняют местами некоторые элементы нашего массива. Если маркером пронумеровать наклейки, то несложно будет проследить, какие именно. Но вообще-то можно это сделать, начертив на бумаге развёртку куба (в дальнейшем все головоломки я буду называть именно кубами, вне зависимости от их формы).
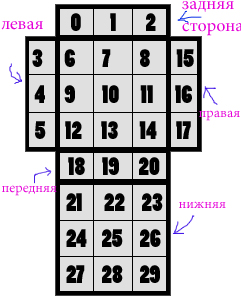
Движение R меняет наклейки 15<->17, 11<->26, 20<->2, 8<->23, 14<->29. Аналогично расписываются оставшиеся три движения. Наконец, нам нужно условие того, что куб собран. Очевидно, это условие будет выглядеть примерно так:
if (s[0]==s[1]&&s[1]==s[2]&&s[3]==s[4]…
Но для оптимизации лучше оформить его в виде функции, которая будет возвращать false сразу, как только наткнётся на не устраивающую на ситуацию:
bool issolvedfloppy()
{
for (int i=6; i<14; i++) if (s[i]!=s[i+1]) return false;
for (int i=0; i<2; i++) if (s[i]!=s[i+1]) return false;
for (int i=3; i<5; i++) if (s[i]!=s[i+1]) return false;
for (int i=18; i<20; i++) if (s[i]!=s[i+1]) return false;
return true;
}
Как вы уже догадались, не обязательно проверять все 6 сторон; достаточно проверить эти четыре — тогда куб точно будет собран. Ну вот и всё, теперь можно приступать к самому перебору.
Прикинув, что эту штуку в принципе можно собрать за 7-10 ходов, я сделал 10 вложенных циклов (от рекурсии пришлось отказаться, так как многократные вызовы функций — лишние прерывания, сильно тормозящие перебор). Циклы по переменным w[i] идут от -1 до 3, где -1 — не делать ничего, 0 — сделать R и тп. В итоге получилось что-то такое:
for (w[10]=-1; w[10]<=3; w[10]++)
for (w[9]=-1; w[9]<=3; w[9]++)
...
for (w[2]=-1; w[2]<=3; w[2]++)
for (w[1]=0; w[1]<=3; w[1]++) {
for (i=10; i>0; i--) floppyTurn(w[j]);
if (issolvedfloppy()) printSolution(w);
}
Ну и всё, после десяти минут дебаггинга получил нормально работающую программку, после чего добавил туда другие головоломки и пользовательский интерфейс. Сделал для неё сайтOAproject.ru, выложил всё туда, в т.ч. и исходники.
Автор: mr_salik








