Пролог: Концепции Boost
Часть 1: Подключение ассоциированных типов без вмешательства в интерфейс исходного класса
Часть 2: Завершаем реализацию поддержки концепций
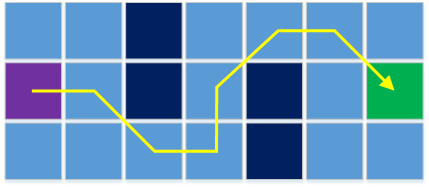
В прошлых статьях цикла описывался процесс адаптации класса клеточного игрового поля под концепции графов boost. Сейчас рассмотрим собственно то, ради чего все затевалось — поиск пути на клеточном поле. Реализация поиска boost позволяет достаточно тонко настраивать алгоритм, в этой статье будет приведет только один пример такой параметризации — возможность задавать различную длину ребер графа.
С описания параметра и начнем. Требуется создать карту весов ребер, которая удовлетворяет концепции ReadablePropertyMapConcept. Реализуется она достаточно просто — нужно определить несколько типов и оператор [], который на основе ключа-ребра, возвращает его длину. Для простоты расчеты будут опущены — примем размер всех ребер равным единице.
struct EdgeWeightMap {
typedef double value_type;
typedef value_type reference;
typedef Edge key_type;
typedef boost::readable_property_map_tag category;
reference operator[](key_type e) const {
return 1;
}
};
С помощью typedef определяются тип ключа (Edge), тип возвращаемого значения (double) и метка, по которой boost сможет понять, что из карты можно получать значения (boost::readable_property_map_tag). Edge и другие пользовательские типы определены в первой части статьи.
Далее нужно реализовать требуемую концепцией функцию. Но сначала введем короткие псевдонимы типов (для себя)
typedef boost::property_map<GameField, boost::edge_weight_t>::const_type EdgeWeightMapConst;
typedef boost::property_traits<EdgeWeightMapConst>::reference EdgeWeightMapValueType;
typedef boost::property_traits<EdgeWeightMapConst>::key_type EdgeWeightMapKey;
Функция должна возвращать значение из карты по ключу
EdgeWeightMapValueType get(EdgeWeightMapConst pMap, EdgeWeightMapKey pKey) {
return pMap[pKey];
}
Теперь можно задать карту весов ребер. Обратите внимание — объявление делается в пространстве имен boost.
namespace boost
{
template<>
struct property_map< GameField, edge_weight_t > {
typedef EdgeWeightMap type;
typedef EdgeWeightMap const_type;
};
}
Проверяем концепцию
boost::function_requires<boost::ReadablePropertyMapConcept<EdgeWeightMap, Edge> >();
Можно еще задать свойства вершин — этого мы делать не будем, однако придется создать заглушку, чтобы boost мог сгенерировать карту для вершин по умолчанию. Для этого достаточно указать тип свойств вершин, пусть это будет тип индекса вершины
namespace boost {
template <> struct vertex_property_type<GameField>
{
typedef boost::graph_traits<GameField>::vertex_descriptor type;
};
}
Это определение также должно располагаться в пространстве имен boost.
Реализуем поддержку нашим графом еще одной концепции — ReadablePropertyGraphConcept, т.е. «граф со свойствами». Для этого потребуется задать две функции. Первая создает карту свойств графа
EdgeWeightMapConst get(boost::edge_weight_t, const GameField& graph)
{
return EdgeWeightMapConst();
}
Обратите внимание, в данной статье веса ребер не рассчитываютcя (равны 1), поэтому и указатель на граф в ней сохранять незачем, соответственно и параметр graph не используется. Также зададим функцию определения веса ребра
EdgeWeightMapValueType get(boost::edge_weight_t tag, const GameField& g, EdgeWeightMapKey e)
{
return get(tag, g)[e];
}
На этом с очередной концепцией закончено, можно выполнить проверку
boost::function_requires<boost::ReadablePropertyGraphConcept<GameField, Edge, boost::edge_weight_t> >();
Алгоритм поиска пути A* относится к классу информированных, а, значит, ему можно (и нужно) помочь. Для этого определим эвристику, которая позволит найти более эффективные направления поиска. Эвристика представляет собой функтор, определяющий насколько заданная вершина далека от целевой. Используется эвклидова метрика
class GameFieldHeuristic: public boost::astar_heuristic<GameField, int>
{
public:
GameFieldHeuristic(const GameField& gameField, Vertex goal)
: mGameField(&gameField)
{
std::pair<int, int> goalPosition = getCoordinates(goal, gameField);
mGoalX = goalPosition.first;
mGoalY = goalPosition.second;
};
int operator()(Vertex v) {
std::pair<int, int> position = getCoordinates(v, *mGameField);
int dx = mGoalX - position.first;
int dy = mGoalY - position.second;
int result =dx * dx + dy * dy;
return result;
}
private:
int mGoalX;
int mGoalY;
const GameField* mGameField;
};
Класс достаточно прост — в конструктор ему передается игровое поле и индекс целевой вершины. По индексу вычисляются координаты вершины на клеточном поле (подробнее об этом рассказано в первой части статьи). Для алгоритма важно увеличение или уменьшение расстояние — точное значение не требуется, поэтому вычисляется квадрат расстояния (квадратный корень в формуле опущен).
Ну и, наконец, создадим класс, который сможет просигнализировать о найденном решении. Сигнализировать будем посредством возбуждения исключения FoundGoal.
struct FoundGoal {};
Создадим класс-посетитель, метод которого examine_vertex вызывается для каждой вершины, до которой дошел алгоритм. Как только окажемся в целевой вершине — возбудим исключение
struct AstarGoalVisitor : public boost::default_astar_visitor {
AstarGoalVisitor(Vertex goal)
: mGoal(goal)
{
}
void examine_vertex(Vertex u, const GameField&) {
if (u == mGoal) {
throw FoundGoal();
}
}
private:
Vertex mGoal;
};
Наконец, пишем функцию поиска пути из одной точки графа в другую. В качестве параметров она принимает координаты исходной и целевой вершин, а также ссылку на граф
typedef std::list<NextStep> StepsList;
StepsList findPath(int sourceX, int sourceY, int targetX, int targetY, const GameFieldMap& graph) {
GraphVertex source = getVertex(sourceX, sourceY, graph);
GraphVertex destination = getVertex(targetX, targetY, graph);
std::vector<GraphVertex> predecessor(num_vertices(graph));
std::vector<edge_weight_map_value_type> dist(num_vertices(graph));
StepsList result;
try {
astar_search(graph, source, GameFieldHeuristic(graph, destination),
boost::visitor(AstarGoalVisitor(destination)).
predecessor_map(&predecessor[0]).
distance_map(&dist[0]));
} catch (FoundGoal f) {
for (int i = destination; i != source; i = predecessor[i]) {
std::pair<int, int> coordinates = getCoordinates(i, graph);
result.push_front(NextStep(coordinates.first, coordinates.second));
}
}
return result;
}
Функция переводит координаты вершин в целочисленные индексы. Затем создается вектор predecessor, из которого будет извлекаться результат и вектор расстояний dist.
Остановлюсь не нескольких моментах. Во-первых, вызов функции поиска astar_search. Вначале ничего не предвещает — идут обычные параметры: граф, исходная точка, эвристика, но потом начинается конструкция через точку вместо запятой. Это не опечатка. Для функций с большим количеством необязательных параметров boost предлагает свой способ передачи именованных аргументов (чтобы не запутаться), тонкости механизма к статье не относятся, лишь несколько замечаний.
- Названия всех параметров определены в пространстве имен boost, однако указывать его нужно лишь один раз вначале цепочки
- Параметры передаются следующим образом: пишется название параметра, далее в скобках — значение, параметры разделяются точкой
- Порядок параметров может быть любым
Если мы попадаем в блок catch — путь найден. Записан он в вектор predecessor, в виде списка предшествующих вершин. Т.е на позиции predecessor[vertex] находится индекс вершины, из которого мы попадаем в vertex. Перебирая таким образом предшественников один за одним, можно получить более привычный путь — последовательность вершин, которые нужно пройти из пункта А в пункт Б. Результат записывается в список result.
Автор: vadim_ig