
4 октября прошел финальный раунд крупнейшей в России ежегодной олимпиады по спортивному программированию Russian Code Cup. Победителем Russian Code Cup 2014 и обладателем главного приза — $10000 — стал Геннадий Короткевич. Второе место занял Петр Митричев — он получил $5000. Третьим финишировал Егор Куликов, его денежный приз составил $3000. Также в этом году впервые были награждены все участники, вошедшие в первую десятку: обладатели 4-10 мест получили по $1000.
Финал прошел в новом для чемпионата онлайн-формате. В отличии от оффлайнового финала прошлого года, участникам сейчас не пришлось приезжать в Москву, а все предложенные задачи финалисты решали онлайн, в комфортной для них атмосфере. За звание лучшего программиста сражались 50 финалистов, преодолевших квалификацию и отборочный тур. 23 человека из финалистов этого года, участвовали в финале RCC 2013 года.
Интересные факты финала
Самая простая задача — A, ее решили 45 финалистов. Самая сложная — F, по ней не было ни одной попытки. Если рассматривать только решенные задачи, то самой сложной была задача E, ее решили только 3 финалиста, причем первым это сделал Евгений Капун. А Алексей Шлюнкин решил только эту задачу.
Финалисты использовали для решения задач только 2 языка программирования!
C++ — 254 решения, из них 91 принято
Java — 52 решения, их них 24 принято
Первое правильное решение — Петр Митричев на 23 минуте, это самый сложный финал по этому показателю.
Победитель — Геннадий Короткевич — сдал пятую задачу за 1 минуту 51 секунду до конца контеста и вышел на первое место. Сдав пятую задачу, его могли бы опередить Петр Митричев, Егор Куликов или Дмитрий Джулгаков.
Яков Длугач сдал 3 задачи за последний час, две за последние 16 минут и ворвался в десятку на 7 место.
Разбор задач
Задача A. Игра
Ограничение по памяти: 256 мегабайт
Король Байтландии проводит ежегодную интеллектуальную игру. По правилам игры все участники делятся на две команды, и каждому из игроков сообщается набор подсказок. Во время проведения игры, участники могут обмениваться подсказками по следующим правилам: Каждый игрок первой команды может подойти к одному игроку второй и запросить у него подсказку, которую он еще не знает. Если таких подсказок несколько, участник второй команды сообщает ему любую на свой выбор. Каждый участник первой команды может спросить подсказку только у одного игрока второй команды, при этом к игроку второй команды может обратиться несколько игроков. Первая команда выигрывает, если ей удастся собрать все подсказки. Помогите ее капитану узнать, сможет ли его команда собрать все подсказки, вне зависимости от ответов второй команды.
Формат входных данных. В первой строке входного файла записаны три целых числа n, m (1 ≤ n, m ≤ 500) и k (1 ≤ k ≤ 5000) — размеры команд и количество подсказок соответственно. Следующие n+m строк содержат информацию о подсказках имеющихся у игроков в начале игры в следующем формате. Первое число в строке соответствует количеству подсказок у игрока, а следующие числа содержат номера подсказок — натуральные числа не превосходящие k.
Формат выходных данных. Если первая команда может собрать все подсказки, в первой строке выходного файла выведите 1. На следующей строке выведите n чисел, для каждого участника первой команды укажите, к кому из игроков второй команды ему обратиться за подсказкой. Если ответов несколько, выведите любой. Если же первая команда не сможет собрать все подсказки в первой и единственной строке выведите 2.
Идея: Анна Малова
Реализация: Анна Малова
Разбор: Анна Малова
Рассмотрим двудольный граф — первая команда, вторая команда. На ребре написано, какими подсказками владеет участник второй команды, которые еще не знает участник первой, то есть разность множеств подсказок участников. Оставим только те ребра, на которых записано одно число. Среди таких ребер оставим только те, на которых записано только одно число.
Используя построенный граф, составим другой двудольный граф: вершинами первой доли являются участники первой команды, вершины второй доли — те подсказки, которые еще неизвестны первой команде. Между двумя вершинами есть ребро, если было ребро в предыдущем двудольном графе, выходящее из той же вершины, на котором была записана эта информация. Если в полученном графе найдётся максимальное паросочетание, значит, первая команда может выиграть. Иначе, первая команда выиграть не может.
Чтобы уложиться в заданные ограничения по времени, для нахождения разности множеств нужно использовать битсет. Кроме этого, перед запуском алгоритма Куна для поиска максимального паросочетания, нужно сравнить размеры долей, если размер доли с подсказками превышает размер доли участников, то сразу выдается ответ 2. Без этой проверки, решение не укладывается в ограничения по времени.
Видеоразбор:
Задача B. Покраска здания
Ограничение по памяти: 256 мегабайт
В одной компании решили перекрасить серую стену своего офиса длиной n метров в корпоративные цвета: синий и оранжевый. Для этого они купили инновационного робота-маляра.
Робот может красить стены в соответствии с записанной в него программой. Программа представляет собой последовательностью команд. Каждая команда задается двумя целыми числами и цветом и сообщает роботу, какой отрезок c стены в какой цвет необходимо покрасить. Например, стену с планом раскраски BBOOO можно получить при помощи программы, состоящей из двух команд: покрасить в синий с первого метра по пятый, а затем — в оранжевый с третьего по пятый.
Одному из программистов компании поручили написать программу, исполнив которую, робот окрашивал бы стены в соответствие с заданной схемой. Он с легкостью справился с заданием и даже написал программу, содержащую в себе минимально возможное количество команд. После этого он задался вопросом: сколько всего существует программ такой же длины, которые покрасят стену в соответствии с планом раскраски?
Формат входных данных. В первой строке задано число T — количество тестов. Далее следуют описания T тестов.
В единственной строке теста дана строка, состоящая из букв B и O, где буква на i-й позиции отвечает за то, в синий или в оранжевый цвет нужно покрасить i-й метр стены.
Суммарная длина строк не превышает 500000.
Формат выходных данных. Для каждого из T тестовых примеров выведите одно число — количество программ программ минимальной длины, приводящих к покраске забора соответствующим образом. Так как ответ может быть большим, то выведите ответ по модулю 109 + 7.
Идея: Виталий Аксёнов
Реализация: Николай Ведерников
Разбор: Николай Ведерников
В задаче требовалось покрасить полоску в два цвета. Мы умеем красить любой подотрезок в какой-то цвет. Требовалось посчитать количество способов раскрасить полоску за минимальное число покрасок.
В данной задаче есть два случая: концы полоски покрашены в один цвет или в разные. Рассмотрим первый случай.
Концы покрашены в один цвет, значит, всего отрезков 2k + 1. Покажем сколько минимум покрасок надо. Рассмотрим конечную раскраску полоски, если последним отрезком мы покрасили отрезок в середине, то общее количество отрезков увеличилось на два (мы разбили какой-то отрезок на два и добавили новый). Таким способом мы можем извлечь k отрезков и в конце останется 1. Итого мы потратили k + 1 ходов. Если в какой-то момент мы взяли отрезок не из середины, а с края, мы потратим больше ходов, чем надо.
Теперь посчитаем количество способов. Рассмотрим конечную раскраску и последним ходом мы красили отрезок в середине, тогда количество способов выбрать этот отрезок равно общему число отрезков минус крайние, итого 2k — 1. Тем самым мы свели задачу к задаче меньшего размером. Продолжая таким способом, мы получим итоговый ответ (2k — 1) · (2k — 3) ·… · 3 · 1, что равно (2k — 1)!!..
Рассмотрим случай, в котором концы покрашены в разные цвета, тогда всего отрезков 2k. Рассмотрим конечную раскраску полоски. Пусть в начале мы l раз извлекали отрезки из середины, а потом извлекли отрезок с краю. Тогда мы потратили l + 1 и у нас осталось 2k-2l-1 отрезков, причём концы оказались одинакового цвета. По предыдущим рассуждениям мы не сможем раскрасить это быстрее, чем за k-l. Итого: k+1 ходов. Кроме того, отсюда следуют факт, что мы первым ходом красим, отрезок с одного из концов.
Теперь посчитаем количество способов. Назовём первый отрезок черным. Пусть первым ходом мы покрасили отрезок с левого края. Переберем докуда он покрасит, а всё, что справа от него, надо будет покрасить в белый, по нашим рассуждениям. Заметим, что теперь у нас получились две предыдущие задачи, у которых концы покрашены в один цвет. Пусть в левом отрезке l черных отрезков, тогда ответ на этом отрезке будет ((2l — 1) — 2)!!, а на правом ((2k — (2l — 1)) — 2)!!.. Кроме того, мы можем можем красить отрезки из левой половины и из правой в любом порядке. То есть произведение отрезков надо ещё умножить на choose(l — 1, k), так как мы уже один отрезок покрасили, значит нам осталось сделать ещё k покрасок, а в левой осталось сделать l — 1 покрасок. Кроме того, первый отрезок мы могли красить и дальше, потому что мы поверх всё равно покрасим правым отрезком. А таких вариантов равно длина правой части. Итого, для фиксированого числа l ответ будет равен ((l — 3)!!) · ((2k — 2l -1)!!) · choose(l — 1,k) · (suff_lenl). Таким образом переберем l и просуммируем. Аналогично посчитаем для другого конца.
Если предподсчитать факториалы и обратные факториалы по модулю, то для одного l мы сможем отвечать за O(1). Итоговое время работы — O(n).
Видеоразбор:
Задача C. Задача о рюкзаке
Ограничение по памяти: 256 мегабайт
В качестве домашнего задания по информатике Пете и Васе задали написать программу, решающую задачу о рюкзаке. Задача формулируется следующим образом: даны N вещей с весами ai, возможно ли выбрать подмножество вещей суммарным весом, равным в точности W?
Петя и Вася успешно справились с заданием, получив Accepted в проверяющей системе. Но при обсуждении задачи выяснилось, что Петя и Вася использовали разные подходы к решению.
Выяснилось, что Вася на самом деле считал количество способов выбрать подмножество вещей весом W, а при выводе ответа сравнивал это количество с нулем. Для упрощения реализации Вася считал не само количество способов, а его остаток от деления на некоторое число m. Петя тут же заявил, что решение Васи неверно, но не смог придумать тест, на котором оно выдает неверный ответ. Сможете ли вы найти такой тест?
По заданному m придумайте тест для задачи о рюкзаке, в котором число способов набрать вес W делится на m без остатка.
Формат входных данных. Единственная строка входного файла содержит целое число m (1 ≤ m ≤ 1018) — модуль, по которому производились вычисления в программе Васи.
Формат выходных данных. Если такого теста не существует, выведите единственное число -1. Иначе, в первой строке выведите через пробел два целых числа N и W (1 ≤ N ≤ 200, 1 ≤ W ≤ 500). В следующей строке выведите N целых чисел ai (1 ≤ ai ≤ W).
Идея: Борис Минаев
Реализация: Артем Васильев
Разбор: Артем Васильев
В данной задаче требуется найти такой тест для задачи о рюкзаке, что количество способов набрать вес W делится на число M.
Далее будем считать W равным 500. Основная конструкция авторского решения основывается на генерации такого набора n вещей небольшого веса так, чтобы их сумма была меньше W/2. Подсчитаем для этого набора количество способов набрать подмножество вещей с суммарным весом k для всех k от 0 до W/2 и обозначим это число за ck. Потребуем, чтобы для нашего набора любое число от 1 до 1018 представлялось как сумма не более, чем 200 — n чисел ck.
Предположим, что существует такой набор вещей, чтобы для каждого x было такое k, что ck = 2x, то такое свойство было бы очевидно: для каждого x, если двоичная запись M содержит единицу на позиции x, мы добавим вещь с весом W — x в наш набор. Поскольку сумма вещей, добавленных до этого шага, была меньше W/2, то легко видеть, что количество способов получить вес W равно M. Заметим, что такой процесс можно описать следующим жадным алгоритмом: пока M больше нуля, мы находим максимальное ck ≤ M, добавляем вещь с весом W — k и вычитаем из M число ck.
К сожалению, такой набор вещей получить трудно, поэтому необходимо придумать какой-то другой набор вещей, обладающий тем свойством, что вышеописанный жадный алгоритм находит решение для любого M. Для этого возьмем набор вещей со случайным небольшим весом и суммой меньше W/2. Можно проверить и убедиться, что если мы выберем наш набор таким образом и посчитаем для него числа ck, то жадный алгоритм с большой вероятностью вернет корректное разбиение любого числа M на слагаемые ck. Таким образом, можно построить набор вещей, удовлетворяющий этому свойству, и с помощью жадного алгоритма добавить вещей таким образом, чтобы количество способов собрать W стало равным 0 по модулю M.
Видеоразбор:
Задача D. Организация сети
Ограничение по памяти: 256 мегабайт
В одной прогрессивной стране полным ходом идёт развитие информационных технологий! Ударными темпами были проложены магистрали, которые будут использоваться для передачи данных. Для простоты контроля за потоками данных и экономии средств на прокладку, магистрали были проложены таким образом, что данные могут дойти от любого города до любого другого единственным образом.
Однако, недостаточно лишь проложить провода, нужно также разработать алгоритмы маршрутизации. В ходе обсуждений была следующая модель маршрутизации данных: k городов объявляются ключевыми точками и каждый из них переименовывается в «Серверград-i». После этого, каждый город получает сетевой адрес. Сетевым адресом города v будет массив из k элементов, в котором i-й элемент равен количеству городов, через которые должен пройти трафик, чтобы попасть из города v в Серверград-i.
Чтобы проблем с маршрутизацией не было, каждый город должен обладать уникальным адресом. Также, правительству хочется, чтобы Серверградов было как можно меньше. Помогите правительству решить, какие города назначить Серверградами.
Формат входных данных. В первой строке задано число n (2 ≤ n ≤ 100 000) — количество городов в стране. Далее, в n — 1 строке заданы пары городов, между которыми проложена магистраль.
Формат выходных данных. Выведите число k — минимальное число Серверградов, которых хватит для обеспечения корректной маршрутизации всех городов. Далее, выведите k различных целых чисел от 1 до n, где i-е число отвечает за то, какой город будет выбран в качестве Серверград-i-го.
Идея: Борис Минаев
Реализация: Андрей Комаров
Разбор: Андрей Комаров
В задаче было дано дерево и требовалось пометить минимально возможное число вершин так, чтобы вектора расстояний от каждой вершины до выбранных были различны.
Рассмотрим отдельно случай, когда заданное дерево является цепочкой: вершины можно упорядочить так, что первая связана только со второй, последняя только с предпоследней, а остальные только с двумя соседями. Если дерево является цепочкой, то, очевидно, в качестве ответа можно взять один из концов этой цепочки: все вершины будут удалены от него на различные расстояния.
Иначе, в дереве есть вершина степени больше двух. Подвесим дерево за эту вершину. Посчитаем следующую динамику для каждого поддерева: минимальное число меток, которое необходимо поставить в этом поддереве, чтобы вектора расстояний для каждой пары вершин этого поддерева были различны, при условии, что где-то выше корня поддерева есть хотя бы одна помеченная вершина. Назовём значение этой динамики min↑. Заметим, что это не совсем то, что нужно посчитать в задаче, но это совпадёт с задачей, если убрать ограничение на существование выше корня помеченной вершины. Назовём эту динамику min. Заметим, что min↑ ≤ min. Значит, если мы сможем предъявить ответ размера ровно min↑, то это будет ответом на задачу. Решим задачу в два этапа — сначала посчитаем значения min↑, а затем получим ответ такого размера.
Пусть мы хотим посчитать min↑ для какой-то вершины v. Посчитаем эти значения для её поддеревьев. Получили, что в некоторых из них есть хотя бы одна метка, а в остальных меток нет. Пусть количество поддеревьев, в которых меток нет, равно k. Тогда в ответ для v нужно добавить хотя бы k − 1 помеченную вершину (по одной в каждое непомеченное поддерево, кроме одного). Пусть мы добавили меньше. Тогда осталось хотя бы два непомеченных поддерева. Тогда корни этих поддеревьев будут неразличимы: в их поддеревьях помеченных вершин нет, а до всех остальных расстояния одинаковы. Теперь покажем, что этих добавлений хватит. Рассмотрим любые две вершины из разных поддеревьев. Они могут быть либо на одинаковой, либо на разной глубине. Пусть они на разной глубине. Тогда расстояния от них до предполагаемой помеченной вершины над корнем различны (различны длины путей до корня). Пусть они на одинаковой глубине. Тогда, по построению, хотя бы в одном из поддеревьев, в которых эти вершины лежат, есть помеченная вершина. Тогда расстояния до неё от этих двух выбранных вершин будут различны: от той, из чьего поддерева выбрана помеченная вершина, расстояние будет меньше.
Построим теперь ответ размера min↑. У выбранного нами корня хотя бы три ребёнка. Значит, по построению min↑, хотя бы в двух поддеревьях корня есть помеченная вершина. Значит, для каждого поддерева есть помеченная вершина вне этого поддерева. Возьмём её в качестве требуемой min↑ помеченной вершины выше. Тогда ответом будет являться объединение ответов min↑ для всех детей корня.
Все рассмотренные операции можно сделать с помощью одного обхода в глубину. Значит, итоговое время работы — O(n).
Видеоразбор:
Задача E. Булево дерево
Ограничение по памяти: 256 мегабайт
Виталик очень долго думал как решить простенькую задачку, и в процессе придумывания решения нарисовал на доске граф. Этот граф по стечению обстоятельств оказался корневым деревом. В этот момент к доске подошел Боря, и начал записывать в некоторых вершинах дерева выражения, в которых булевым переменным присваивались различные значения.
После этого они ввели правило, по которому для каждой вершины дерева можно определить значение переменной в этой вершине. А именно, если в этой вершине записывалось присваивание этой переменной значения, то используется последнее такое значение. Если таким образом значение определить не удалось, то берется значение этой переменной в ближайшем предке этой вершины, в котором записано присваивание значение этой переменной. Если у вершины нет такого предка, значит значение не определено.
После нескольких операций они захотели посчитать для заданной переменной в скольких листьях дерева значение этой переменной true, в скольких false, а в скольких не определено. И тут они поняли, что это сложно, и что сделать этого они не могут. Поэтому они просят вас помочь им, и после каждого добавления записи о присваивании значения переменной, определять, для скольких листьев значение этой переменной равно true, для скольких false, а для скольких не определено.
Формат входных данных. В первой строке задано число T — число тестов. Далее идёт описание T тестов.
В первой строке теста даны два натуральных числа n и m (1 ≤ n, m ≤ 105), где n – количество вершин заданного дерева, а m – количество добавлений новых записей о присваивании значения переменной. Во второй строке даны n чисел, где i-е число это номер предка i-й вершины. Для корня это число равно нулю. Гарантируется, что вам дано именно дерево. Далее идут m строк – описания записей. В каждой из этих строк содержатся три числа: v – номер вершины, x – номер переменной и b – ноль либо единица, если значение переменной равно false или true соответственно. Номер переменной – это целое положительное число, не превосходящее 105.
В каждом наборе входных данных сумма всех n и сумма всех m не превышают 105.
Формат выходных данных. Для каждого из тестовых примеров выводите m строк, содержащие по три числа – количество листьев дерева, для которых значение только что написанной переменной равно true, false и не определено, соответственно.
Идея: Борис Минаев
Реализация: Демид Кучеренко
Разбор: Виталик Аксенов
Для начала сведём нашу задачу к задаче об одной переменной. Заведём по дереву на каждую переменную, в которых в изначальном состоянии будут находиться корень изначального дерева и ссылка на него. Ссылка в дереве у нас всегда будет указывать на вершину, в чьём поддереве мы сейчас находимся. Обойдём наше дерево обходом в глубину. Если мы заходим в вершину, в которой выставлена какая-то переменная, то мы создаём у вершины в соответствующем дереве нового ребёнка и переставляем ссылку на него. Если мы выходим из вершины, то мы переставляем ссылку в соответствующем дереве на её предка. Мы сжали деревья. Нужно ещё не забыть хранить в каждой вершине количество листьев в её поддереве.
Мы теперь будем решать задачу на дереве для одной переменной. Будем обрабатывать все запросы на данную переменную последовательно. Нам нужно уметь делать две вещи:
- на сколько листьев влияет только эта вершина;
- найти ближайшего предка, в котором выставлено какое-то значение для данной переменной.
Если мы реализуем это, обрабатывать запрос не очень сложно:
- находим количество листьев, на которые влияет эта вершина — x;
- находим ближайшего предка, в котором выставлено какое-то значение для данной переменной — p;
- если в p такое же значение, что и в нашей вершине, то количество не меняется;
- если в p другое значение, нежели в нашей вершине, то количество меняется на x;
- если p не существует, то количество меняется на x* то количество «неизвестных» листьев уменьшается на x;
- в p нужно уменьшить количество влияемых листьев на x
Чтобы реализовать запросы нужно развернуть дерево в дерево отрезков, где можно делать запрос на поддереве. Тогда запросы первого вида очень легко обрабатывать с помощью суммы в поддереве. Для поиска правильного предка сделаем следующее: когда делаем запрос в вершину, мы прибавляем ко всем вершинам в поддереве, кроме неё, единицу, то есть говорим, что они покрыты ещё одной вершиной. Тогда чтобы найти предка, мы будем искать двоичным подъёмом первую позицию, в которой значение отличается на единицу — она и будет искомым предком.
Итоговое время работы: O(mlog2n), где n — размер дерева, m — количество запросов.
Видеоразбор:
Задача F. Робот
Ограничение по памяти: 256 мегабайт
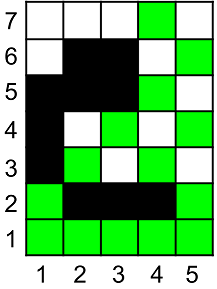
По прямоугольному клеточному полю, состоящему из n столбцов и m строк, путешествует робот. Он может начать свое путешествие в любой клетке первой строки. Далее он может совершить некоторое (возможно, нулевое) количество ходов. Пусть робот стоит в столбце x и строке y, тогда за один ход он может перейти либо в клетку (x + 1, y + 1), либо в клетку (x — 1, y + 1). Конечно, робот не может выходить за границы поля.
Путешествие робота осложняется тем, что на поле есть прямоугольные преграды, стороны которых параллельны сторонам поля. Робот не может пойти в клетку, которая покрывается преградой. Никакие две преграды не пересекаются, но могут касаться.
Вам необходимо посчитать количество клеток, в которые может попасть робот.
Формат входных данных. В первой строке задано число T — количество тестов. Далее следует описание T тестов.
В первой строке теста дано два целых числа n и m (1 ≤ n, m ≤ 109) — количество столбцов и строк на поле. В следующей строке задано одно целое число k (1 ≤ k ≤ 105) — количество преград на поле. В следующих k строках задано описание преград. Каждая такая строка состоит из четырех целых чисел x1, y1, x2, y2, обозначающих координаты противоположных углов преграды (1 ≤ x1 ≤ x2 ≤ n, 2 ≤ y1 ≤ y2 ≤ m). Гарантируется, что преграды не пересекаются.
Общее количество преград во входном файле не превышает 105.
Формат выходных данных. Для каждого из T тестовых примеров выведите одно число — количество клеток, которые может посетить робот.
Идея: Борис Минаев
Реализация: Борис Минаев
Разбор: Борис Минаев
В задаче необходимо было посчитать количество клеток, которые достижимы из первой строки поля. Основная сложность заключается в том, что размеры каждой стороны поля могут достигать 109 клеток.
Во-первых, из-за того, что робот совершает ходы по диагонали, удобно отдельно рассматривать клетки разной чётности. Робот может достичь все клетки первой строки поля. Будем увеличивать y и пересчитывать достижимые клетки. Удобнее всего хранить множество достижимых клеток для строки в виде объединения непересекающихся отрезков. Тогда можно легко пересчитывать множество при переходе к следующей строке. А именно, к каждому отрезку добавится по одной клетке с каждой стороны. Некоторые отрезки, возможно, объединятся в один, а некоторые пересекутся с границами поля или преградами.
Научимся эффективно изменять это множество отрезков. Лучше всего хранить его в структуре данных, которая позволяет за O(logn) находить отрезок, который пересекает заданную координату. Дополнительно, у каждого отрезка будем хранить информацию о том, может ли отрезок увеличится влево и вправо. Давайте аккуратно рассмотрим все события, которые могут происходить:
- Два отрезка объединились. Это самый простой случай. Необходимо просто объединить их в структуре данных.
- Отрезок расширился до такой степени, что пересекся с краем поля или преградой. Тогда необходимо поставить пометку в описании отрезка, что он не может больше расти в некоторую сторону.
- Началась преграда. Необходимо рассмотреть все отрезки, которые пересекаются с преградой. Некоторые из них нужно полностью удалить, некоторые обрезать, а некоторые разделить на две части. Также необходимо создать события, которые произойдут, когда соседние отрезки разрастутся настолько, что пересекут текущую преграду.
- Преграда закончилась. Необходимо найти два соседних отрезка и поставить им пометку о том, что они могут расти в направлении прямоугольника. Также необходимо добавить событие, которое должно произойти между соседями. Например, если два соседа являются отрезками, то они могут в некоторый момент объединиться. Если один из них отрезок, а другой — преграда, то они могут пересечься. В остальных случаях ничего добавлять не надо.
Также заметим, что все отрезки необходимо хранить лениво. То есть изменять их размер, а также пересчитывать общее количество достижимых клеток, необходимо только тогда, когда происходит некоторое событие, которое затрагивает данный отрезок.
Время работы решения — O(n log (n)), где n — общее число преград.
Видеоразбор:
Автор: Andrey_Kravchenko








