Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает замечательные результаты, хотя и отсутствует теория сходимости. Используется по умолчанию в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.
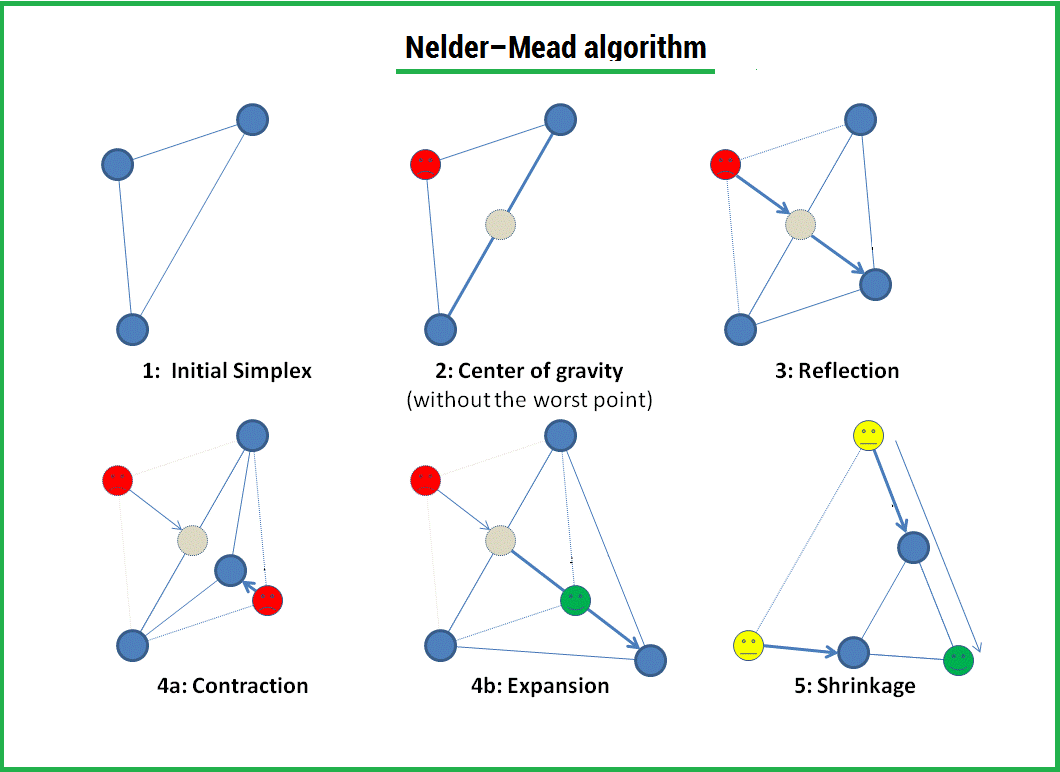
Алгоритм заключается в формировании симплекса (simplex) и последующего деформирования в направлении минимума, посредством трех операций:
1) Отражение (reflection);
2) Растяжения (expansion);
3) Сжатие (contract);
Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это прямая, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.
Алгоритм
1) Пусть 
функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке: 
, 
, 
.
Сортируем точки по значениям функции 
в этих точках, т.е. получаем двойное неравенство: 
≤ 
≤ 
.
Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:
b = 
, g = 
, w = 
, где best, good, worst — соответственно.
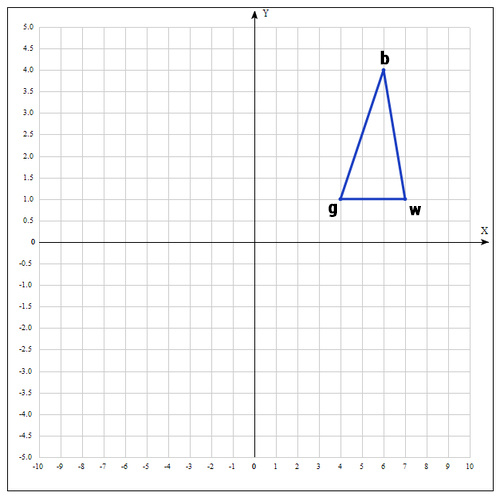
2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:
В более общем виде можно записать так:
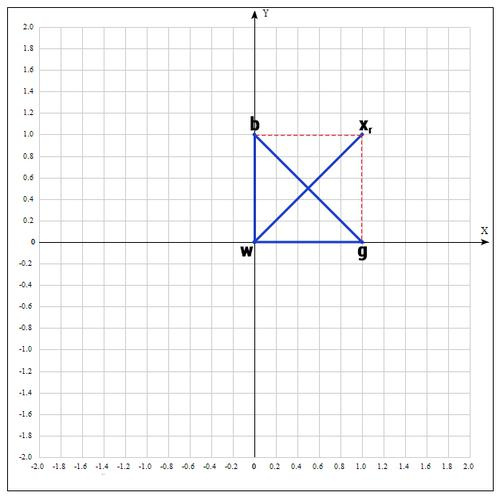
3) Применяем операцию отражения:
Находим точку 
, следующим образом:
Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если f(
) < f(g), то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.
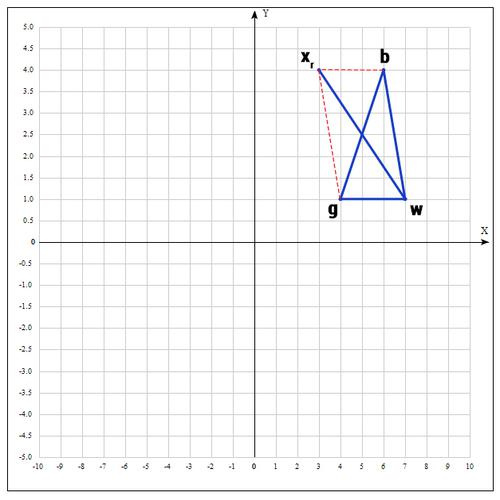
4) Применяем операцию растяжения:
Находим точку 
следующим образом:
В качестве γ принимаем γ = 2, т.е. расстояние увеличиваем в 2 раза.
Проверяем точку 
:
Если f(
) < f(b), то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке 
.
Далее заменяем точку w на 
, в итоге получаем:
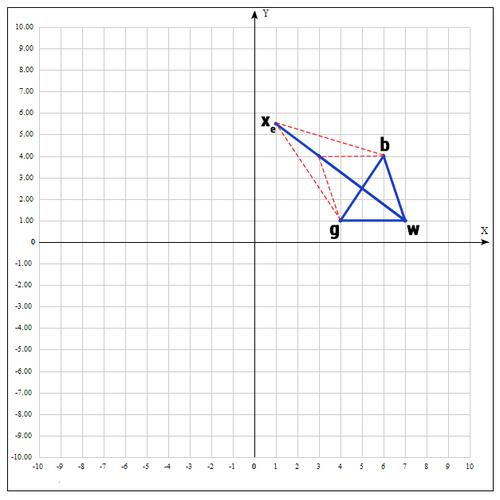
5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.
Пробуем найти хорошую точку 
:
Коэффициент β принимаем равным 0.5, т.е. точка 
на середине отрезка wmid.
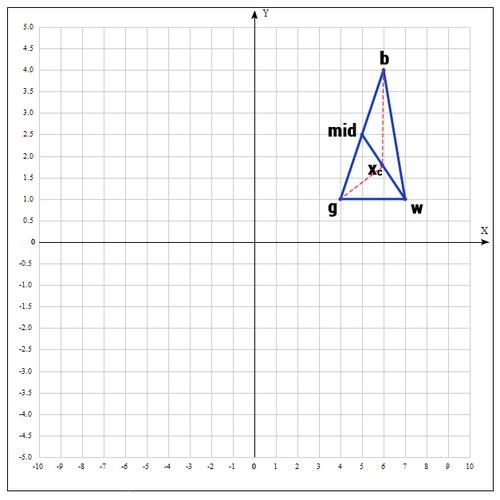
Существует еще одна операция — shrink (сокращение). В данном случае, мы переопределяем весь симплекс. Оставляем только «лучшую» точку, остальные определяем следующим образом:
Коэффициент δ берут равным 0.5.
По существу передвигаем точки по направлению к текущей «лучшей» точке. Преобразование выглядит следующим образом:
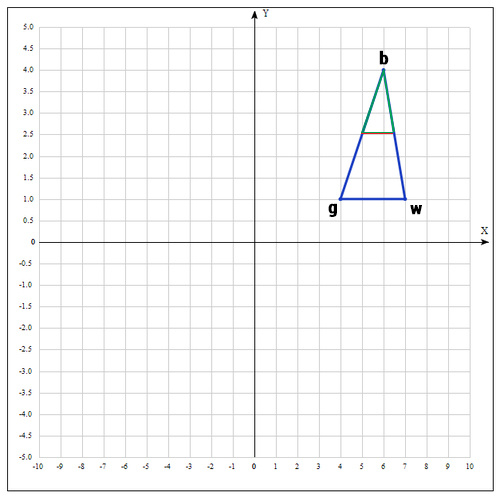
Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.
Алгоритм заканчивается, когда:
1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.
Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:
Выбор первой точки 
поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из 
, на небольшом расстоянии вдоль направления каждого измерения:
,
где 
— единичный вектор.
определяется таким образом:
= 0.05, если коэффициент при 
в определении 
не нулевой.
= 0.00025, если коэффициент при 
в определении нулевой.
Пример:
Найти экстремум следующей функции: 
В качестве начальных возьмем точки:
Вычислим значение функции в каждой точке:
Переобозначим точки следующим образом:
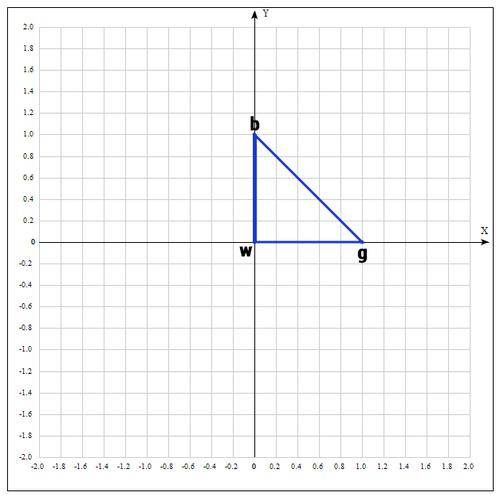
Находим середину отрезка bg:
Находим точку 
(операция отражения):
если α=1, тогда:
Проверяем точку 
:
, т.к. 
пробуем увеличить отрезок (операция растяжения).
если γ = 2, тогда:
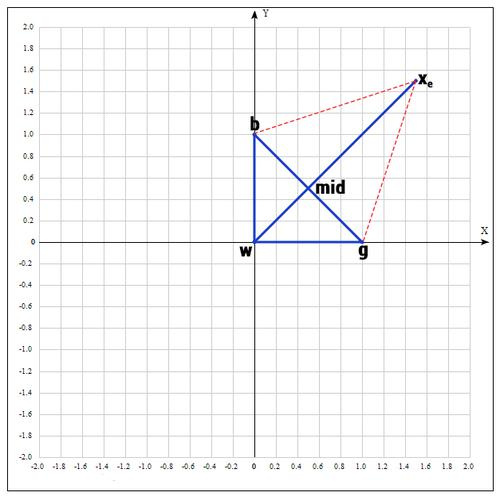
Проверяем значение функции в точке 
:
Оказалось, что точка 
«лучше» точки b. Следовательно мы получаем новые вершины:
И алгоритм начинается сначала.
Таблица значений для 10 итераций:
| Best | Good | Worst |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
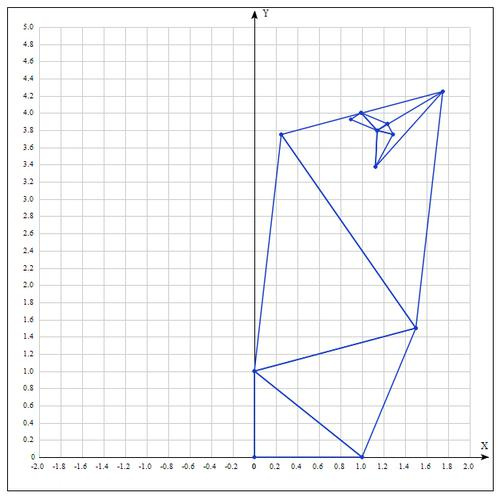
Аналитически находим экстремум функции, он достигается в точке 
.
После 10 итераций мы получаем достаточно точное приближение: 
Еще о методе:
Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).
С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.
Реализация на языке программирования python:
Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.
class Vector(object):
def __init__(self, x, y):
""" Create a vector, example: v = Vector(1,2) """
self.x = x
self.y = y
def __repr__(self):
return "({0}, {1})".format(self.x, self.y)
def __add__(self, other):
x = self.x + other.x
y = self.y + other.y
return Vector(x, y)
def __sub__(self, other):
x = self.x - other.x
y = self.y - other.y
return Vector(x, y)
def __mul__(self, other):
x = self.x * other
y = self.y * other
return Vector(x, y)
def __truediv__(self, other):
x = self.x / other
y = self.y / other
return Vector(x, y)
def c(self):
return (self.x, self.y)
def f(point):
x, y = point
return x**2 + x*y + y**2 - 6*x - 9*y
def nelder_mead(alpha=1, beta=0.5, gamma=2):
v1 = Vector(0, 0)
v2 = Vector(1.0, 0)
v3 = Vector(0, 1)
for i in range(10):
adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())}
points = sorted(adict.items(), key=lambda x: x[1])
b = points[0][0]
g = points[1][0]
w = points[2][0]
mid = (g + b)/2
xr = mid * 2 - w
if f(xr.c()) < f(g.c()):
w = xr
else:
if f(xr.c()) < f(w.c()):
w = xr
c = (w + mid)/2
if f(c.c()) < f(w.c()):
w = c
if f(xr.c()) < f(b.c()):
xe = xr * 2 - mid
if f(xe.c()) < f(xr.c()):
w = xe
else:
w = xr
if f(xr.c()) > f(g.c()):
xc = mid * (1 - beta) + w * beta
if f(xc.c()) < f(w.c()):
w = xc
v1 = w
v2 = g
v3 = b
print(b)
nelder_mead()
P.S. Может у кого-нибудь есть реализация алгоритма на других языках программирования? С радостью расширю статью, естественно указав автора реализации.
Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)
Автор: FUNNYDMAN
