Это заметка о том, что на основании алгоритма генерации спектров (о котором было рассказано в статье «Спектроскоп Салтана...») создан тестовый сервис, обратиться к которому может любой желающий.

Под катом — инструкция по использованию сервиса и его возможностей.
Общие принципы генерации спектров (проекций) приведены в упомянутой выше статье. Картинки чем-то напоминают фигуры Хладни.
Интерфейс
Интерфейс сервиса предельно прост, ориентирован на настольные компьютеры и не адаптирован под мобильные экраны.
Управление генерацией состоит в изменении параметров, приведенных в правой части экрана на панели управления. Панель управления разбита на несколько секций.
Набор точек (Set)
Здесь задается геометрия расположения базового набора точек.
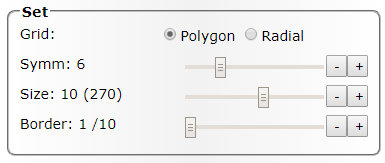
Grid: Тип сетки. Доступно два типа — на основе правильных многоугольников (Polygon) и на основе окружностей (Radial).
Symm: Тип симметрии, количество сторон базового многоугольника. Доступный диапазон — от треугольника до 16-угольника. При большом количестве сторон картинки спектров становятся мало отличимыми друг от друга (многоугольники превращаются в круг).
Size: Размер стороны многоугольника. Минимальный равен 2 (две точки). Справа от размера в скобках указано общее количество спектральных линий данного набора, которое на единицу меньше количества точек (поскольку исключен нулевой спектр).
Border: Параметр, который позволяет удалять точки из центра набора. В пределе можно оставить только точки на границе (окаймление) многоугольника.
Начальным набором точек является 6-угольник со стороной 10 точек.
Управление функцией (Function)
Доступны два параметра, влияющих на генерацию функции расстояния между точками.

Общий вид используемой функции: 
здесь 


Данные параметры позволяют «деформировать» базовый набор, делать его выпуклым или вогнутым.
Управление картинкой (Plot)
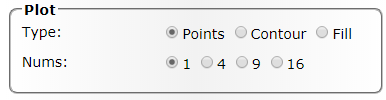
Тут два параметра.
Type: Определяет режим вывода — тип выводимой картинки. Три доступных типа — точки (Point), контуры (Contour) и заполнение цветом (Fill). Это ключевой параметр, от которого зависит интерпретация других.
Nums: Количество одновременно выводимых спектров. От 1 до 16. При выводе нескольких спектров можно указать параметры, индексы которых будут также линейно меняться с номером спектра. Такие параметры задаются в секции «Spectr».
Управление спектром (Spectr)
Здесь настраиваются три основных индекса, влияющих на отображение спектров: P, Z и S.
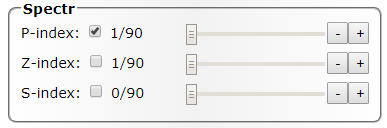
Справа от каждого имени индекса находится флажок (чекбокс), определяющий участие индекса в развороте, если выводится одновременно более одного спектра. Несмотря на то, что можно активировать одновременно все три флажка (разворота), лучше этого не делать, а варьировать только какой-то один индекс.
P-index: Это номер проекции. Общее количество доступных проекций выводится после обратной черты. Например, надпись «5/90» означает, что текущий P-index равен 5, а всего доступно 90 разных проекций. Количество проекций — это количество вырожденных спектров.
Z-index: Данный индекс можно рассматривать как вес или высоту точек проекции. Значение индекса влияет на распределение цвета точек в режиме Points, или на форму контуров (областей) в режимах Contour и Fill.
S-index: Еще один индекс, связанный с невырожденными уровнями спектра. В режиме Points он влияет на распределение размера выводимых точек. В режимах Contour и Fill от данного индекса зависит маскировка триангуляции.
В отличие от других индексов значение S-индекса начинается с 0. Нулевое значение означает отключенный индекс (не активен).
Общее количество доступных индексов Z и S определяется количеством невырожденных уровней спектра.
Стиль/размер (Style)

Size: В режиме Points параметр стиля определяет размер точек. В режиме Contour — количество выводимых уровней (контуров). При большом значении параметра генерация контуров замедляется.
Управление цветом (Color)
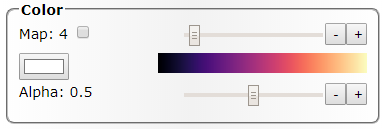
Map: Выбор цветовых палитр (карт). Флажок инвертирует палитру.
Alpha: Значение насыщенности цвета.
Также доступен выбор фона картинок. Некоторые спектры хорошо звучат на темном фоне.
Действия меню
В текущей версии доступно:
- Save: Сохранение текущих параметров спектра.
- Load: Восстановление спектра по ранее сохраненным параметрам.
- Reset: Сброс всех параметров к «заводским».
Немного, да. Но лучше, чем ничего.
Можно получать спектры и сохранять их в файлы изображений на своем компьютере.
Примеры спектров
Не все спектры имеют художественную ценность. Но если немного попрактиковаться, то можно научиться получать довольно интересные.
Точки
При выводе мозаик размер точек фиксирован, а распределение цвета задается Z-индексом. В первой статье уже приводился узор в виде мозаики. Здесь мы просто развернули мозаику по Z-индексу:

Если же варьировать размер точек, то можно получить вот такие «кружева»:

Контуры
Пример очень простых контуров на 6-угольном базисе:
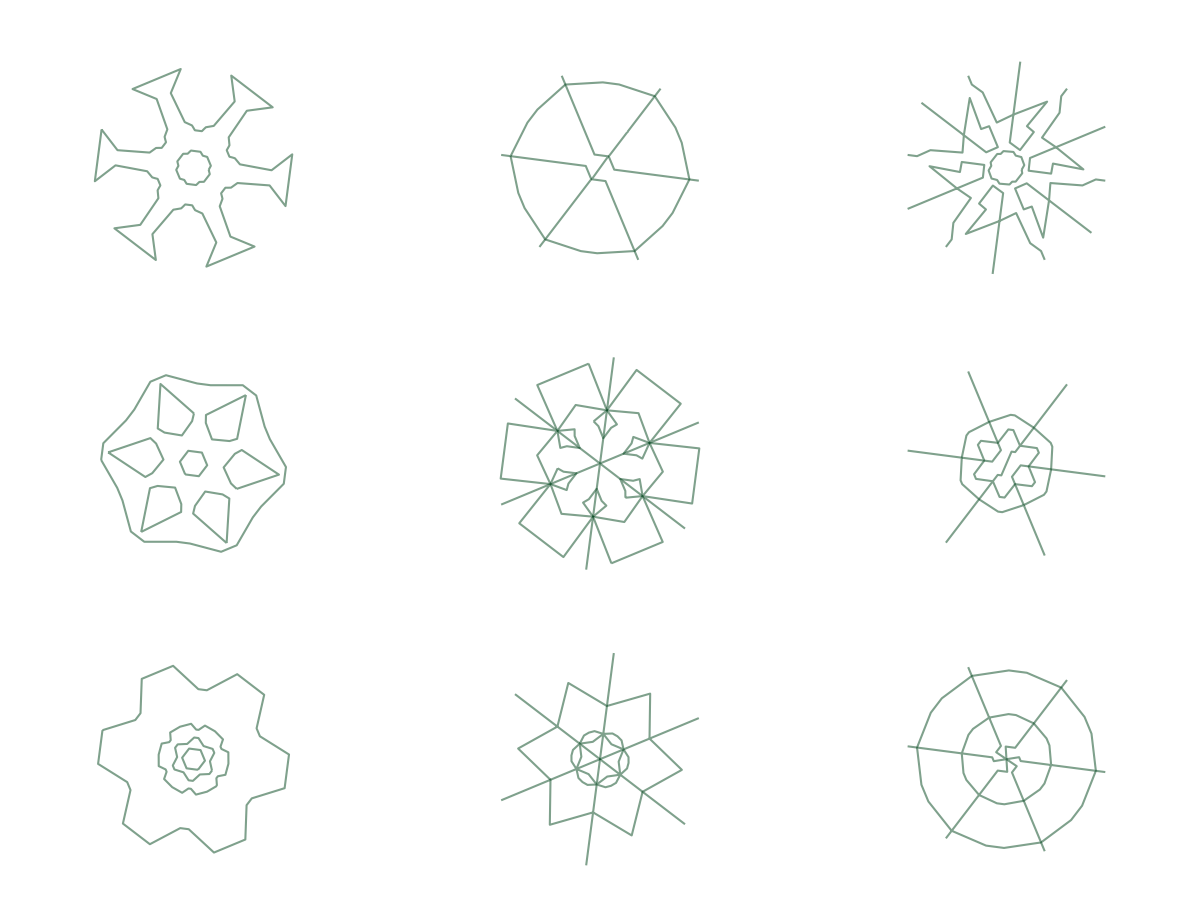
Именно своей примитивностью они и привлекают.
Если немного усложнить (добавить количество точек набора), то тогда можно получить примерно такое:
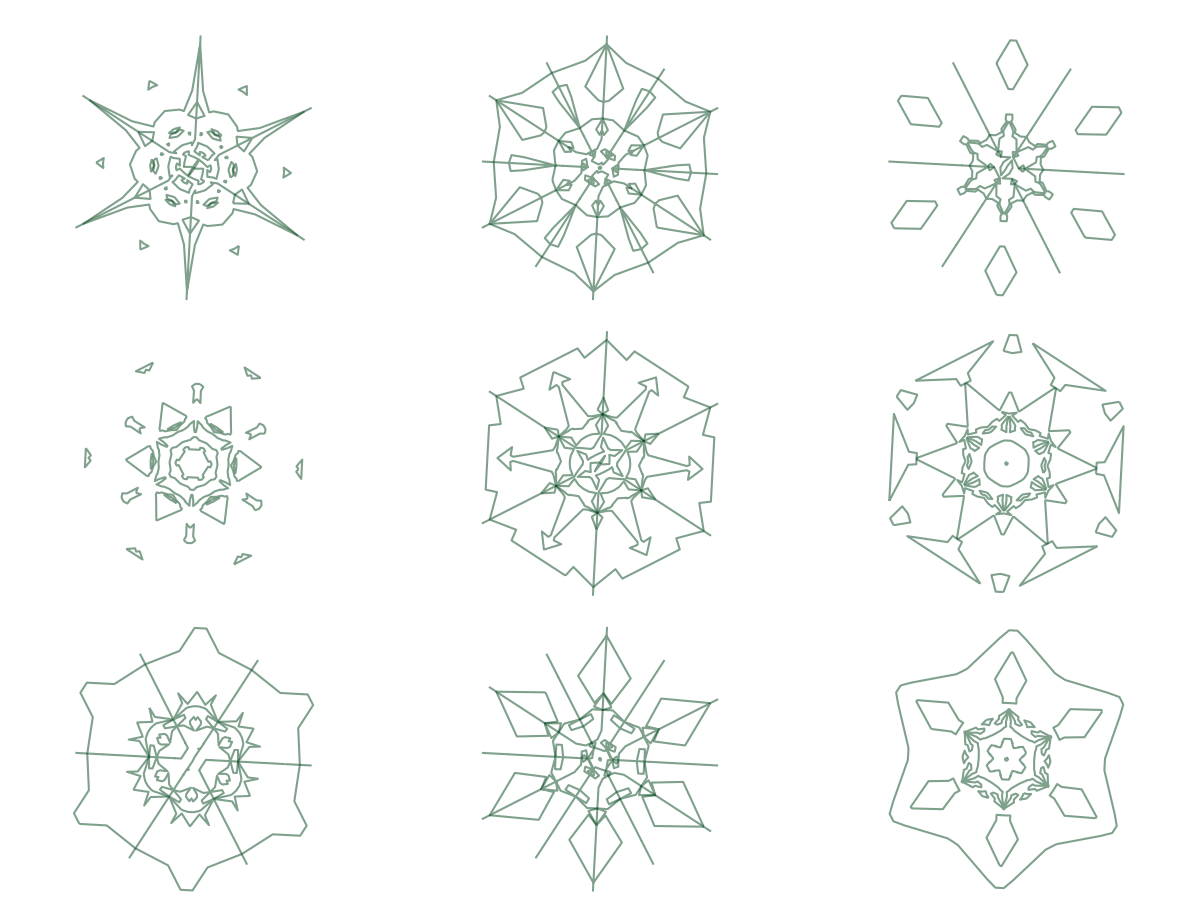
А на 10-угольном базисе такое:

При желании всегда можно добавить цвета. Вот, например, красные 5-конечные звезды для буденновок:
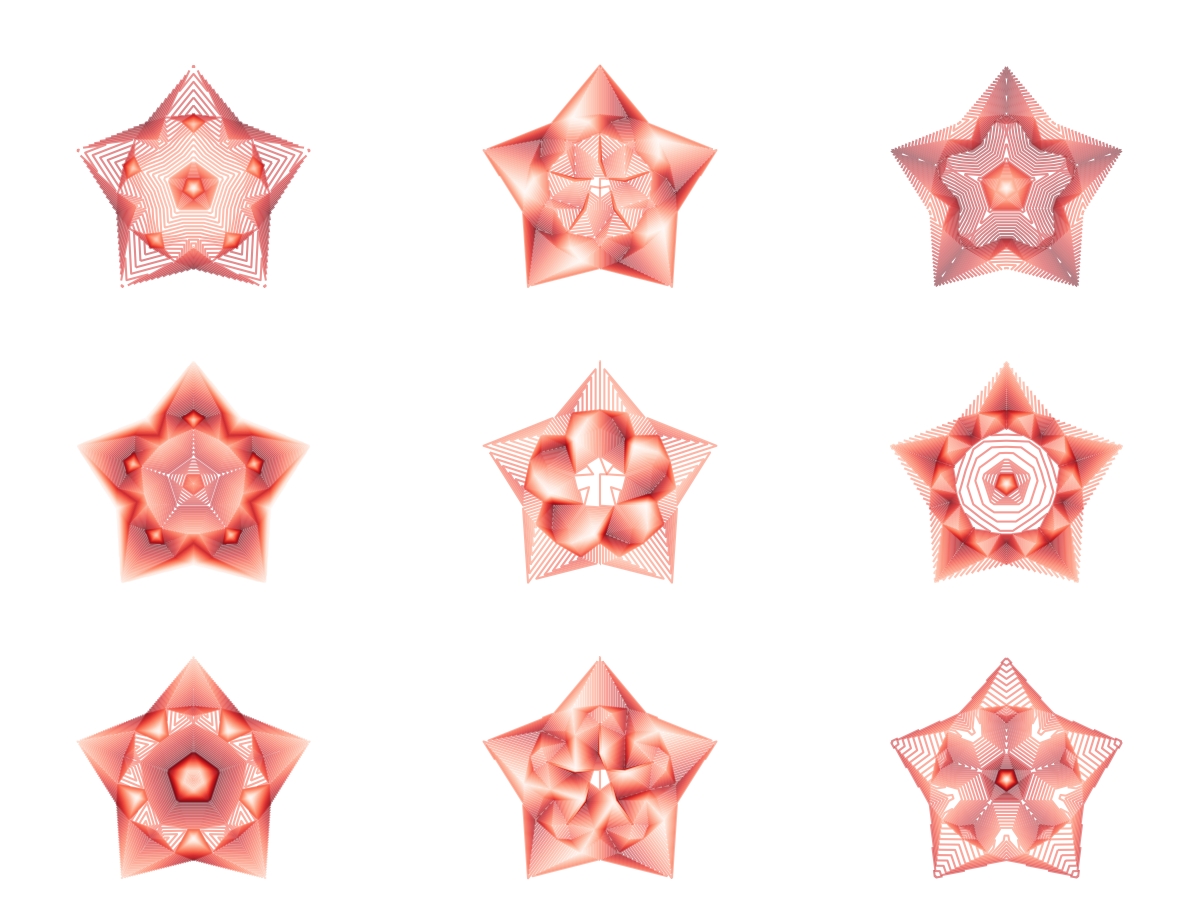
В целом у меня все. Пользуйтесь и экспериментируйте!
Надеюсь, но не гарантирую, что сервис выдержит. Критичные и смешные баги будем исправлять, расширение функционала — под вопросом.
Всех с днем знаний, без которых мы бы этих картинок не увидели!
 — размер стороны многоугольной решетки и
— размер стороны многоугольной решетки и — количество сторон многоугольника.
— количество сторон многоугольника.Удобно ввести параметр
 — это количество точек на секторе.
— это количество точек на секторе.Тогда общее количество точек базового многоугольника
 будет равно:
будет равно: (+1 — это центральная точка)
(+1 — это центральная точка)Общее количество уровней спектра на единицу меньше количества точек:

Часть уровней двукратно вырождена — проекции. Их количество обозначим как
 . Количество невырожденных уровней обозначим
. Количество невырожденных уровней обозначим  .
.Тогда имеет место инвариант:

Далее. Количество проекций определяется формулой:


Оставшееся количество невырожденных уровней зависит от четности параметра симметрии:




Самое странное тут — это последняя формула. При фиксированном размере стороны многоугольника количество вырожденных уровней не зависит от уровня симметрии (количества сторон), а зависит только от его четности. Наверное, этому есть какое-то простое объяснение, которое нам пока неизвестно.
Автор: dmagin




