Здравствуйте!

В связи с вопросами читателей моей публикации [1] касательно условий возбуждения автоколебаний в механической системе, я решил описать явление возникновения и поддержания автоколебаний подробно, выделив основные области возникновения и применения автоколебаний.

В википедии автоколебания объясняют так [2]:

Незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. При этом частота становится почти равной резонансной.

Автоколебания в технике

Автоколебательная система с запаздыванием (на примере электромеханического звонка)
Приведём пример электромеханического звонка:

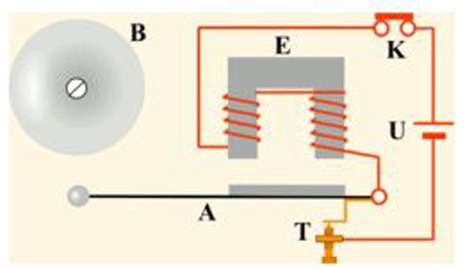
При замыкании цепи кнопкой (К) электромагнит (Е) притягивает ударник, ударник бьёт по звонку и размыкает цепь питания электромагнита, механически связанным с ним контактом (Т) ударник (А) возвращается назад и процесс повторяется.

При рассмотрении процесса возникновения автоколебаний будем считать, что сила, действующая на боёк (А) звонка, изменяется пропорционально изменению тока в RL цепи.

Такое допущение сделано для упрощения рассмотрения, поскольку зависимость силы от тока в обмотке и зазора между бойком и полюсами значительно сложнее [3].

Ниже приведены конструкции электромеханических звонков и их упрощённая электрическая схема:

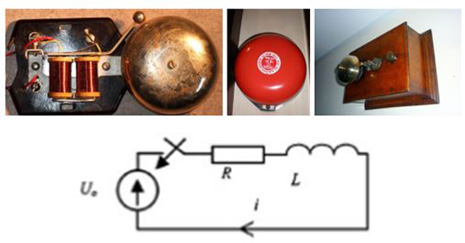
Боёк колеблется относительно установленного зазора согласно соотношению A*sin (w*t).
Решив численным методом дифференциальное уравнение RL цепи с начальными условиями
для замыкания и размыкания контакта, наложив на эти решения колебания бойка, получим:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 
R=100;L=0.07;E=100;tm=L/R;T=0.0280;w=2*np.pi/T # параметры RL цепи и частота бойка w    
def dydt(y, t):# функция диф. уравнений для  численного решения
         return -y/tm
def dydt1(y1, t):
         return -y1/tm+E/L
plt.title('Колебательные процессы в звонке', size=12)
y = odeint(dydt, E/R, np.linspace(0,T/4,300))# ток (сила) при размыкании RL, y(0)=E/R
plt.plot(np.linspace(0,T/4,300), y,'b',linewidth=2,label='Сила Fp=Km*Ip')# график 
y1 = odeint(dydt1, 0,  np.linspace(T/2,3*T/4,300))# ток (сила) при замыкании RL, y(0)=0 
plt.plot( np.linspace(T/2,3*T/4,300), y1,'g',linewidth=2,label='Сила Fz=Km*Iz')
t2=np.linspace(0,T,300)
y2=(E/R)*np.sin(w*t2)# уравнение колебаний бойка
plt.plot(t2, y2,"--r",linewidth=2,label='Колебания бойка ')
t3=np.linspace(0,T/4,300)
t4=np.linspace(T/2,3*T/4,300)
y3=[0 for i in t3]
y4=[0 for i in t4]
plt.plot(t3, y3,"--k",linewidth=3,label='Запаздывание Fp от бойка ')
plt.plot(t4, y4,"--k",linewidth=3,label='Запаздывание Fz  от бойка')
plt.legend(loc='best')
plt.grid(True)
plt.show()

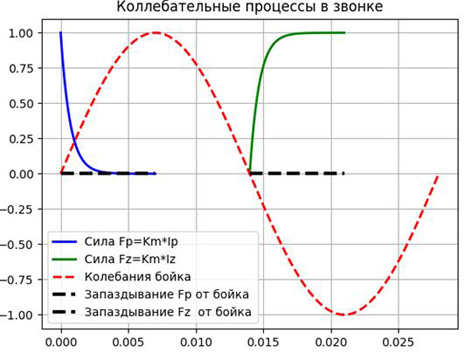
Для приближенной теории будем считать, что сила Fτ, выраженная последовательностью прямоугольных импульсов, которые возникает и исчезает мгновенно, но не в момент срабатывания контакта, а с запаздыванием τ=L/R. Добавим Fτ на график, получим:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 
R=100;L=0.07;E=100;tm=L/R;T=0.0280;w=2*np.pi/T # параметры RL цепи и частота бойка w    
def dydt(y, t):# функция диф. уравнений для  численного решения
         return -y/tm
def dydt1(y1, t):
         return -y1/tm+E/L
plt.title('Колебательные процессы в звонке', size=12)
y = odeint(dydt, E/R, np.linspace(0,T/4,300))# ток (сила) при размыкании RL, y(0)=E/R
plt.plot(np.linspace(0,T/4,300), y,'b',linewidth=2,label='Сила Fp=Km*Ip')# график 
y1 = odeint(dydt1, 0,  np.linspace(T/2,3*T/4,300))# ток (сила) при замыкании RL, y(0)=0 
plt.plot( np.linspace(T/2,3*T/4,300), y1,'g',linewidth=2,label='Сила Fz=Km*Iz')
t2=np.linspace(0,T,300)
y2=(E/R)*np.sin(w*t2)# уравнение колебаний бойка
plt.plot(t2, y2,"--r",linewidth=2,label='Колебания бойка ')
def con_n(f):
         z=0
         if  np.sin(0)<=np.sin(f)<np.sin(T/4):                 
                  z=E/R
         elif np.sin(T/4)<= np.sin(f)<np.sin(3*T/4):                  
                  z=0
         elif np.sin(3*T/4)<=np.sin(f)<np.sin(T+tm):
                  z=E/R
         return z         
y3=[con_n(q) for q in t2]
plt.plot(t2, y3,"k",linewidth=3,label='Импульсы силы ') 
plt.legend(loc='best')
plt.grid(True)
plt.show()

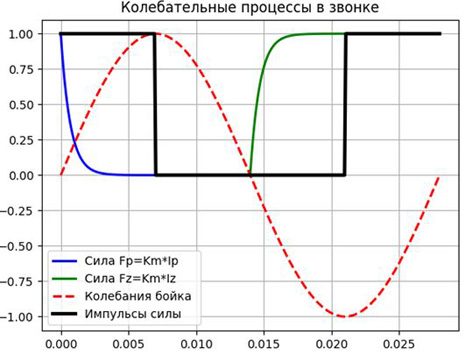
Обозначим амплитуду силы Fτ через Aτ, получим разложения этой силы в ряд Фурье [4] (учитывая что x=a∙sin(ω∙t), для первых двух членов ряда:

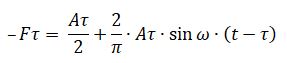
Будем считать, что постоянная составляющая силы Aτ/2 компенсируется регулировкой.
Тогда уравнение для колебаний бойка с учётом его приведенной массы m, трения r и изгибной жёсткости k примет вид:

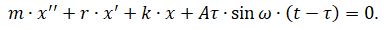(1)

Разделим обе части на массу бойка, введем обозначения,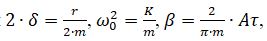 получим:

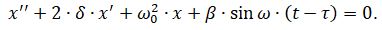(2)

Для того, чтобы получить аналитические соотношения для частоты и амплитуды колебаний бойка, решим (2) приближённым методом [5]. Преобразуем (2) к виду:

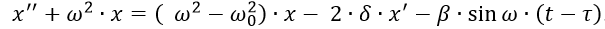(3)

Подставив в (3) 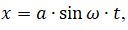при условии: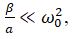
пропуская промежуточные выкладки получим соотношения для частоты и амплитуды автоколебаний:

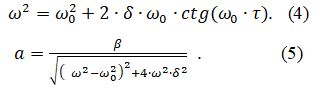
На основании приведенных соотношений можно сделать вывод, что, при отсутствии самоиндукции, звонок работать не может, поскольку при L=0 нет запаздывания τ=0. Таким образом, при нулевом запаздывании автоколебания не возможны.

Автоколебания в измерительной технике (на примере механического резонатора вибрационных плотномеров)

Механические резонаторы в виде трубок пластин или цилиндров широко используются в вибрационных плотномерах, внешний вид которых приведен на рисунках:

Будем рассматривать резонатор c сосредоточенными эквивалентными параметрами: массой 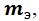жесткостью 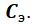и трением, характеризуемым коэффициентом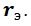

Такая замена вполне допустима в ограниченной области частот при соблюдении равенства собственных частот колебаний обеих систем, а также равенства потерь энергии и обусловленных ими затуханий.

Запишем систему уравнений, описывающих движение резонатора в замкнутой системе возбуждения:

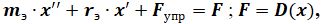
где: F- сила воздействия системы возбуждения на резонатор;
D(x)- неизвестный оператор обратной связи, подлежащий определению; Fупр — упругая восстанавливающая сила резонатора, которая в общем случае может описываться нелинейной функцией; х — поперечное смещение эквивалентной массы.

Воспользуемся выражением кубической упругой характеристики резонатора:

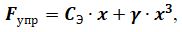
где γ — коэффициент, характеризующий отклонение реальной упругой характеристики от линейной.

Преобразуем записанную систему равенства к виду:

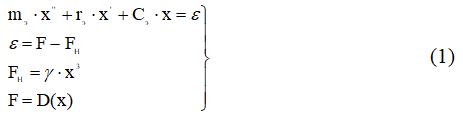
где 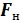— нелинейная составляющая упругой силы.

Структурная схема автоколебательной системы, работа которой характеризуется уравнениями, (1) приведена на рисунке:

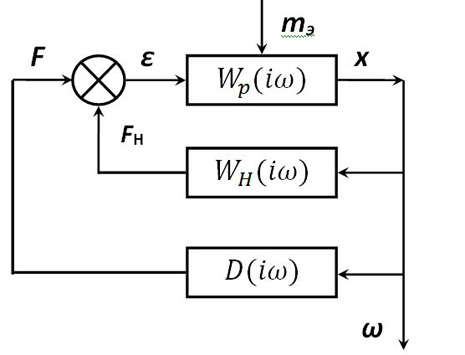
Схема содержит нелинейное звено, выполняющее функцию корректирующей обратной связи линейного резонатора, имеющего частотную характеристику:

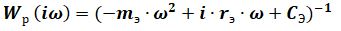
Для решения задачи синтеза оптимальной системы возбуждения, воспользуемся методом гармонической линеаризации [6].

Механические резонаторы являются высокодобротными колебательными системами, которые можно рассматривать как узкополосные фильтры с выходным сигналом вида: x~A∙cos⁡(ω∙τ), где A— амплитуда колебаний резонатора; ω — частота колебаний, близкая к резонансной [7].

Поэтому для нелинейного элемента справедливо соотношение:

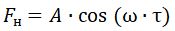
Пренебрегая третьей гармоникой, отфильтрованной линейной частью резонатора, частотную характеристику линеаризованного звена нелинейной упругости механического резонатора можно в виде:

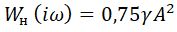
Рассмотрим уравнение для первой гармоники колебаний линеаризованной системы:

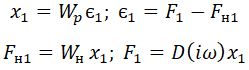
Для определения вида частотной характеристики D(iω), обеспечивающей совместность этой системы, исключим промежуточные переменные прямой подстановкой их выражений через другие переменные. В результате получим:

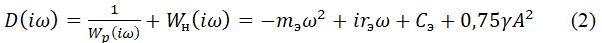
Из соотношения (2) определим смещение фазы, осуществляемое системой возбуждения:

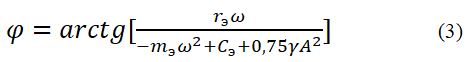
Нетрудно установить, что частота автоколебаний не будет зависеть от трения 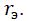при сдвиге фазы φ=π/2, тогда:

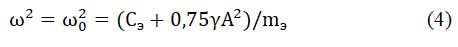
При этом условии из (2) следует, что система возбуждения должна быть дифференцирующим звеном D(iω)=(i*rэ* ω) т.е.

Из (5) следует, что частотная характеристика цепи обратной связи системы возбуждения должна быть пропорциональна коэффициенту трения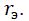

Система возбуждения состоит из трех элементов, D(iω)=Dп* Dу* D(в ), характеризующих частотные характеристики: приемника Dп, усилителя Dу и возбудителя D(в ) колебаний. Приемник является дифференцирующим – Dп=Kп* i*ω, а возбудитель усилительным
звеном – Dв=Kв.

Для выполнения условия (5) усилитель должен иметь частотную характеристику:

Коэффициент усиления должен меняться вместе с изменением трения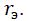
Звено с переменным коэффициентом усиления можно реализовать простейшей нелинейностью типа двухпозиционного реле, имеющей частотную характеристику по первой гармонике [6]:

где 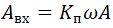— амплитуда первой гармоники на входе усилителя; 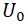— выходное напряжение усилителя, подаваемое на возбудитель колебаний.

Из (6) и (7) можно получить выражение для амплитуды установившихся автоколебаний резонатора:

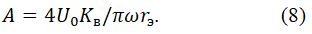
Для устранения этого влияния амплитуды на частоту резонатора можно стабилизировать амплитуду A варьированием напряжения U0 с помощью регулятора, стабилизирующего амплитуду входного сигнала Aвх, поступающего с приемника колебаний.

Из изложенного можно сделать вывод, что частота автоколебаний резонатора вибрационного измерительного преобразователя не будет зависеть от трения при сдвиге фазы φ=π/2, когда система возбуждения является дифференцирующим звеном, и не будет зависит от амплитуды автоколебаний при стабилизации входного сигнала этого звена.

Автоколебания в радиотехнических генераторах (на примере решения уравнения
Ван-дер-Поля)

Обобщённая схема радиотехнического генератора автоколебаний приведена на рисунке:

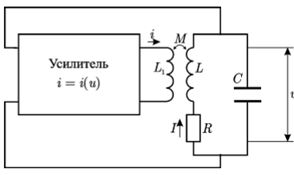
Механизм возбуждения автоколебаний в генераторе можно качественно описать следующим образом. Даже при отсутствии напряжения на выходе усилителя напряжение в контуре испытывает случайные флуктуации. Они усиливаются усилителем и вновь поступают в контур через цепь обратной связи.

При этом из шумового спектра флуктуаций будет выделяться составляющая на собственной частоте высокодобротного контура. Если энергия, вносимая в контур таким образом, превосходит энергию потерь, амплитуда колебаний нарастает.

Основной моделью, описывающей автоколебания в радиотехническом генераторе, является уравнение Ван-дер-Поля. Приведём уравнение Ван-дер-Поля к виду, содержащему единственный управляющий параметр с безразмерными переменными:

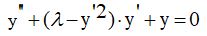
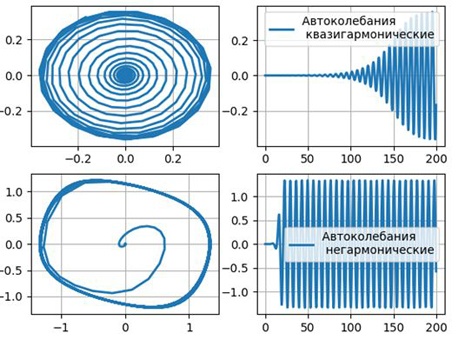
Получим фазовые портреты (слева) и временные реализации колебаний (справа) осциллятора Ван-дер-Поля: λ =0.1, λ =1.1

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def f(y, x):
                y1, y2 = y              
                return [y2,(0.1-y2**2)*y2-y1]
x= np.linspace(0,200,601)
y0 = [0.0001,0.0001]
[y1,y2]=odeint(f, y0, x).T
plt.subplot(221)
plt .plot(y1,y2,linewidth=2)
plt .grid(True)
plt.subplot(222)
plt .plot(x,y1,linewidth=2, label='Автоколебания  n квазигармонические')
plt.legend(loc='best')
plt .grid(True)
def f_1(y, x):
                y1, y2 = y              
                return [y2,(1.1-y2**2)*y2-y1]
x= np.linspace(0,200,601)
y0 = [0.0001,0.0001]
[y1,y2]=odeint(f_1, y0, x).T
plt.subplot(223)
plt .plot(y1,y2,linewidth=2)
plt .grid(True)
plt.subplot(224)
plt .plot(x,y1,linewidth=2, label='Автоколебания n негармонические')
plt.legend(loc='best')
plt .grid(True)
plt.show()

Для λ =10.0

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def f(y, x):
                y1, y2 = y              
                return [y2,(10.0-y2**2)*y2-y1]
x= np.linspace(0,200,601)
y0 = [0.0001,0.0001]
[y1,y2]=odeint(f, y0, x).T
plt.subplot(221)
plt .plot(y1,y2,linewidth=2)
plt .grid(True)
plt.subplot(222)
plt .plot(x,y1,linewidth=2, label='Автоколебания n релаксационные')
plt.legend(loc='best')
plt .grid(True)
plt.show()

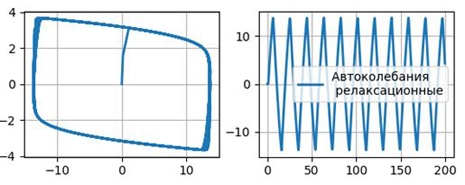
Уравнение Ван-дер-Поля имеет единственную особую точку 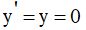, которая является устойчивым узлом при 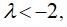устойчивым фокусом при 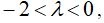неустойчивым фокусом при 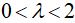и неустойчивым узлом при 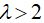. Если выполнено условие самовозбуждения, на фазовой плоскости имеется также предельный цикл, отвечающий режиму периодических автоколебаний.

Химические колебания. Брюсселятор

Важным и нетривиальным примером автоколебательных процессов служат некоторые химические реакции. Химические колебания — это колебания концентраций реагирующих веществ.

К настоящему времени известно достаточно много колебательных реакций. Наиболее знаменитая из них была открыта Б.П. Белоусовым в 1950 г. и позднее детально изучена А.М. Жаботинским. Реакция Белоусова — Жаботинского (БЖ) представляет собой процесс окисления малоновой кислоты при взаимодействии в присутствии ионов в качестве катализатора.

В ходе реакции раствор периодически изменяет свой цвет: голубой — красный — голубой — красный и т.д. Кроме простых периодических колебаний, реакция БЖ демонстрирует (в зависимости от условий эксперимента) множество различных типов пространственно-временной динамики, которые окончательно еще не исследованы.

Предложены различные математические модели реакции БЖ (например, модель Филда, Кереса и Нойеса — «орегонатор»), однако ни одна из них не описывает полностью все детали, наблюдаемые в эксперименте.

Мы рассмотрим более простой модельный пример: гипотетическую химическую реакцию, которая получила название Брюсселятор [8]. Уравнения этой реакции имеют вид:

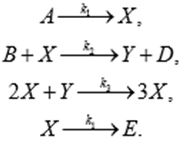
Предполагается, что реагенты A и B имеются в избытке, так что их концентрации можно считать постоянными, а D и E ни в какие реакции не вступают. Составим кинетические уравнения, соответствующие реакции, которые описывают динамику концентраций реагирующих веществ.

Поскольку число актов химической реакции в единицу времени определяется вероятностью столкновения молекул реагентов, скорости изменения концентраций продуктов реакции пропорциональны произведению концентраций соответствующих реагентов с коэффициентами пропорциональности, называемыми константами скоростей реакций. Тогда кинетические уравнения можно записать в виде:

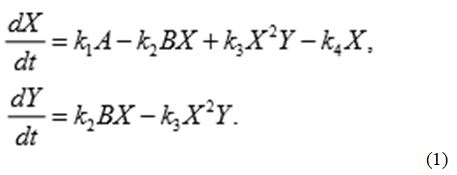
Символами Y,X будем теперь обозначать соответствующие концентрации. Отметим, что из третьего уравнения системы следует, что скорость образования вещества X зависит от его концентрации, т.е. эта стадия реакции носит автокаталитический характер. Приведем уравнения (1) к безразмерному виду, содержащему минимальное число управляющих параметров. Для этого перейдём к новым переменным, 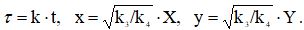Тогда уравнения (1) примут вид:

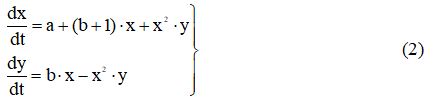
Построим фазовые портреты для: a=1.0; b=2.1; b=3.0;b=5.0

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
b=2.1
def f(y, x):
                y1, y2 = y              
                return [1-(b+1)*y1+(y1**2)*y2, b*y1-(y1**2)*y2]
x= np.linspace(0,100,1001)
y0 = [0.5,1.5]
[y1,y2]=odeint(f, y0, x).T
plt .plot(y1,y2,linewidth=2,label='a=1.0, b=%s'%b)
plt.legend(loc='best')
plt .grid(True)
plt.show()

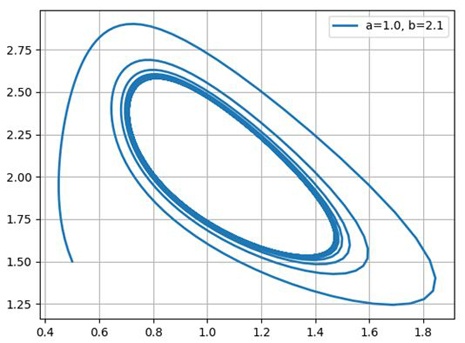
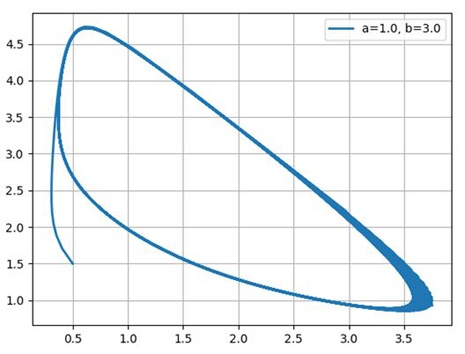
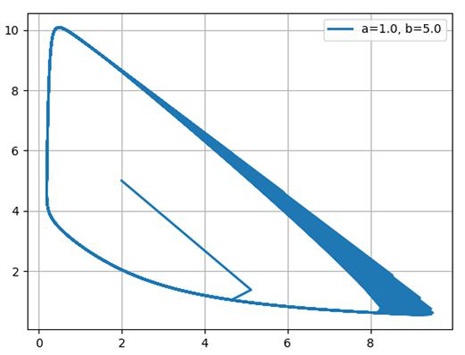
Таким образом, химический осциллятор демонстрирует поведение, типичное для автоколебательных систем и вполне аналогичное, например, осциллятору Ван-дер-Поля.

Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)

В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка.

Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x и y— число жертв и хищников соответственно. Предположим, что относительный прирост жертв y'/x равен a-by, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, -by— потери от хищников.

Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x=0 ) относительная скорость изменения популяции хищников равна y'/y =-c, c>0, наличие пищи компенсирует убывание, и при x>0 имеем y'/y =(-c +d*x), d>0.

Таким образом, система Вольтерра—Лотка имеет вид:

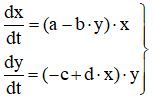
где a, b, c, d >0.

Рассмотрим фазовый портрет системы Вольтерра Лотка, для a=4 b=2.5, c=2, d=1 и графики ее решения с начальным условием x(0)=3, y(0)=1, построенные программой Python для численного решения системы обыкновенных дифференциальных уравнений:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
a=4;b=2.5; c=2; d=1 
def f(y, t):
                y1, y2 = y              
                return [y1*(a-b*y2),y2*( -c+d*y1)]
t = np.linspace(0,10,201)
y0 = [3, 1]
[y1,y2]=odeint(f, y0, t).T
plt.figure()
plt .plot(y1,y2,linewidth=2)
plt .grid(True)
plt.figure()
plt .plot(t,y1,linewidth=2)
plt .plot(t,y2,linewidth=2)
plt .grid(True)
plt.show()

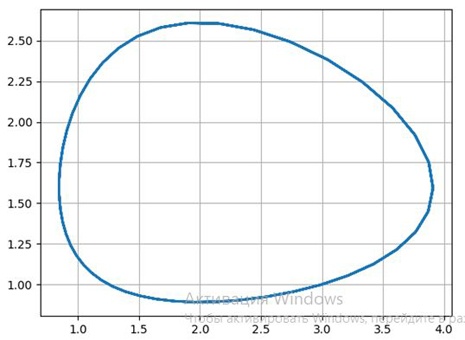
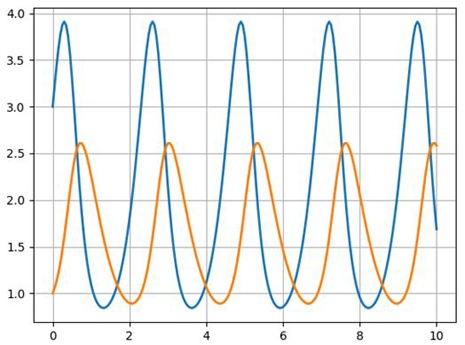
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1, обе популяции сначала растут. Когда число хищников достигает величины b=2.5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать.

Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x=c/d =2 (в этой точке y'=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины y=a/b =1.6 (в этой точке x'=0).

С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и… процесс повторяется снова и снова.

Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.

Спасибо за внимание!!!

Ссылки:

1. Математическая модель вибрационного уровнемера с резонатором в виде консольной эллиптической трубки. ^[1]
2. Автоколебания ^[2]
3. Базовые уравнения задачи синтеза ш-образного электромагнита. ^[3]
4. О классификации методов преобразования Фурье на примерах их программной реализации средствами Python. ^[4]
5. Теодорчик К.Ф. Автоколебательные системы. ГИТЛ.,1952 г., 272 с.
6. Метод гармонической линеаризации средствами Python. ^[5]
7. Жуков Ю.П. Вибрационные плотномеры. — М. Энергоатомиздат, 1991. —
144с: ил. — (Б-ка по автоматике; Вып 678)
8. И. Пригожин, Р. Лефевр Брюсселятор М. Наука,1968

Автор: Юрий Тараненко

Источник ^[6]