Иногда помогаю проводить математический анализ у первых курсов и нужно им подбирать задачи, на которых можно набить руку. Да, можно брать задачи из книги. Но что, если не находишь нужных по уровню задач в книгах, которые есть под рукой?
О том, как сделать свой генератор простых задач на нахождение пределов/производных/интегралов и пойдёт речь после ката.
P.s. Опыт создания похожей программы описан в предыдущей части
Как можно увидеть из картинки, задачи будем генерировать в pdf при помощи LaTex. О нем было уже много разных статей, так что вводную часть опущу. Реализовывать и создавать задачи будем через Pascal (но общий алгоритм опишу и спрячу весь код в спойлеры).
Приступим
Для начала нужно определить понятие полинома(многочлена), так как тригонометрические функции опираются именно на многочлен. В составе стандартных операций нужно ввести:
- Сложение многочленов
- Вычитание многочленов
- Перемножение многочленов
- Возведение в натуральную степень
- Перевод в текст Tex-а
- Производная
- Интеграл
st:integer;//степень многочлена
kof:array of real;//коэффициенты при x^i
function into(x:real):real;
class function operator+(a,b: polynomial): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(a,b: polynomial): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a,b: polynomial): polynomial;
var i,j,stn:integer;
rez:polynomial;
begin
stn:=a.st+b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a:integer; b: polynomial): polynomial;
var i:integer;
begin
for i:=0 to b.st do
b.kof[i]:=a*b.kof[i];
result:=b;
end;
class function operator in(a: polynomial; n:integer): polynomial;
var i:integer;
rez:polynomial;
begin
rez.st:=0;
setlength(rez.kof,1);
rez.kof[0]:=1;
for i:=1 to n do
rez:=rez*a;
result:=rez;
end;
procedure nw(x:integer);
function pltostr:string;//в строковую переменную
procedure derivative;//производная
procedure integral;//интеграл
end;
procedure polynomial.nw(x:integer);
var
i:integer;
begin
st:=x;
setlength(kof,st+1);
for i:=0 to st do
kof[i]:=random(-10,10);
while(kof[st]=0)do
kof[st]:=random(-10,10);
end;
procedure polynomial.integral;
var
i:integer;
begin
setlength(kof,st+2);
for i:=st downto 1 do
kof[i+1]:=kof[i]/i;
kof[0]:=0;
st:=st+1;
setlength(kof,st+1);
end;
procedure polynomial.derivative;
var
i:integer;
begin
for i:=1 to st do
kof[i-1]:=kof[i]*i;
st:=st-1;
setlength(kof,st+1);
end;
Вслед за обычным многочленом потребуется ввести многочлен с корнями (чтобы можно было искать корни или сокращать дроби).
Но тут будет особенность, так как нужно сделать те же самые свойства не только для того же класса, но и для обычного многочлена.
st:integer;//степень многочлена
root:array of integer;//корни многочлена
kof:array of integer;//коэффициенты при x^i
class function operator+(a,b: polynomialwithroot): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator+(a: polynomialwithroot; b:polynomial): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator+(b:polynomial; a: polynomialwithroot): polynomial;
// var i:integer;
// rez:polynomial;
begin
result:=a+b;
end;
class function operator-(a,b: polynomialwithroot): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(a:polynomialwithroot; b:polynomial): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(b:polynomial; a:polynomialwithroot): polynomial;
var i,stn:integer;
rez:polynomial;
begin
if(a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if(i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if(i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a,b: polynomialwithroot): polynomialwithroot;
var i,j,stn:integer;
rez:polynomialwithroot;
begin
stn:=a.st+b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
setlength(rez.root,rez.st);
for i:=0 to a.st-1 do
rez.root[i]:=a.root[i];
for i:=0 to b.st-1 do
rez.root[a.st+i]:=b.root[i];
result:=rez;
end;
class function operator*(a:polynomialwithroot; b:polynomial): polynomial;
var i,j,stn:integer;
rez:polynomial;
begin
stn:=a.st+b.st;
setlength(rez.kof,stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while(rez.kof[stn]=0)do
begin
setlength(rez.kof,stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(b:polynomial; a:polynomialwithroot): polynomial;
// var i,j,stn:integer;
// rez:polynomial;
begin
result:=a*b;
end;
class function operator in(a: polynomialwithroot; n:integer): polynomialwithroot;
var i:integer;
rez:polynomialwithroot;
begin
rez:=a;
for i:=2 to n do
rez:=rez*a;
result:=rez;
end;
procedure nw;
procedure roots(x:integer);
function pltostr:string;
end;
procedure polynomialwithroot.roots(x:integer);
var i:integer;
begin
st:=x;
setlength(root,st);
for i:=0 to st-1 do
begin
root[i]:=random(-5,5);
end;
nw;
end;
procedure polynomialwithroot.nw;
var
i,j,sum:integer;
tk:array of integer;
dop:integer;
begin
setlength(kof,st+1);
setlength(tk,st+1);
for i:=0 to st-1 do
kof[i]:=0;
for i:=0 to st-1 do
begin
for j:=0 to st do
tk[j]:=0;
while(tk[st]=0)do
begin
sum:=0;
for j:=0 to st-1 do
sum:=sum+tk[j];
if(sum=(i+1))then
begin
dop:=1;
for j:=0 to st-1 do
if(tk[j]=1)then
dop:=dop*root[j];
for j:=0 to i do
dop:=-dop;
kof[st-i-1]:=kof[st-i-1]+dop;
end;
tk[0]:=tk[0]+1;
for j:=0 to st-1 do
begin
tk[j+1]:=tk[j+1]+(tk[j] div 2);
tk[j]:=tk[j] mod 2;
end;
end;
end;
kof[st]:=1;
end;
А дальше по однотипному примеру работаем с тригонометрическими функциями (включая логарифм и e^x).
x:polynomial;
s:string;
procedure nw;
procedure derivative;//производная
end;
type cosx= record
x:polynomial;
s:string;
procedure nw;
procedure derivative;//производная
end;
type tgx= record
x:polynomial;
s:string;
procedure nw;
procedure derivative;//производная
end;
type ctgx= record
x:polynomial;
s:string;
procedure nw;
procedure derivative;//производная
end;
type lnx=record
s:string;
x:polynomial;
procedure nw;
procedure derivative;
end;
type ex=record
s:string;
f,x:polynomial;
procedure nw;
procedure derivative;
end;
Заранее оговорюсь, что не буду использовать никаких тригонометрических формул дальше. Это увеличит сложность не только для решения, но и для составления схем задач.
Немного о TeX
Для упрощения работы с TeX был создан отдельный класс, чтобы потом вынести все в отдельный модуль.
Класс отвечает за:
- Создание нового tex файла (создание и вводный блок)
- Построчного добавления текста (в конце строки будет переход на новую строку)
- Создание нового tex файла
- Закрытия tex файла (закрывающий блок и прекращение работы с файлом)
- Создание pdf через установленный на компьютер Tex
- Открытие pdf файла
namefl:string;
procedure newtex(s:string);
procedure add(s:string);
procedure closetex;
procedure createpdf;
procedure openpdf;
end;
implementation
procedure tex.newtex(s:string);
var
t:text;
begin
namefl:=s;
assign(t,s+'.tex');
rewrite(t);
writeln(t,'documentclass[12pt]{article}');
writeln(t,'usepackage{amsmath}');
writeln(t,'%usepackage[rus]{babel}');
writeln(t,'%usepackage[cp1251]{inputenc}');
writeln(t,'begin{document}');
close(t);
end;
procedure tex.add(s:string);
var
t:text;
begin
assign(t,namefl+'.tex');
append(t);
writeln(t,'[');
writeln(t,s);
writeln(t,']');
close(t);
end;
procedure tex.closetex;
var
t:text;
begin
assign(t,namefl+'.tex');
append(t);
writeln(t,'end{document}');
close(t);
end;
procedure tex.createpdf;
var
p:System.Diagnostics.Process;
begin
p:=new System.Diagnostics.Process();
p.StartInfo.FileName:='pdflatex';
p.StartInfo.Arguments:=namefl+'.tex';
p.Start();
end;
procedure tex.openpdf;
var
p:System.Diagnostics.Process;
begin
p:=new System.Diagnostics.Process();
p.StartInfo.FileName:=namefl+'.pdf';
p.Start();
end;
Схема задач
Заранее оговорюсь, что задача на производную и интеграл обратные, так что нужна только одна схема на две задачи.
Пределы
В начале курса математического анализа чаще всего всплывают пределы (при x-> inf): inf/inf, 0/0, inf-inf, a/inf и a/b.
Значит и схемы таких задач должны проверять на вшивость понимание разницы.
1. Пример, где ответ нуль
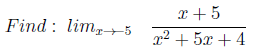
Задание строится по типу P1(x)/P2(x)* при х стремящимся к корню P1(x) (и не является корнем P2(x)).
*P1(x) и P2(x) многочлены с корнями от 1 до 3 (иногда 4-ой) степени (рандомная генерация)
2. Нуль в знаменателе
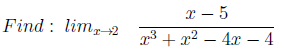
Достаточно просто. По аналогии с первым примером, тут нуль в знаменателе.
3. Нули в числителе и знаменателе
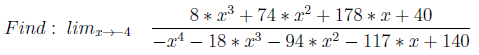
Строятся два многочлена с корнями так, чтобы один корень был у обоих P(x). Тогда при x стремящемся к этому корню будет отношение 0/0. Отсюда необходимость дифференцировать P1(x) и P2(x), чтобы найти правильный ответ.
4. Бесконечность минус бесконечность
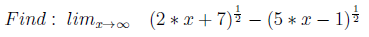
Пример по принципы inf-inf я решил демонстрировать на примере корней (часто встречалось в книжках, но есть и другие примеры).
Тут в основе лежит то, что P3(x)* и P4(x)* одной степени, а решение состоит в том, чтобы домножить и поделить на сопряженное.
*P3(x),P4(x) — многочлены под корнем первой степени
Производные и интегралы
«Берешь и считаешь»
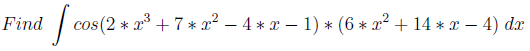
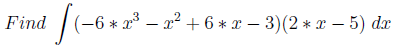
Примеры строятся следующим образом: берется производная функции (многочлен/тригонометрическая функция) и нужно найти её интеграл (по сути первоначально взятую функцию).
Метод хитрого взгляда
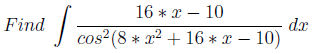
Задачу можно строить различными способами. Один из них взять тригонометрическую функцию T(P(x)) (P(x) многочлен второй или более высокой степени) и перемножить T(P(x)) на производную P(x). Такой прием нужно уметь замечать, чтобы не использовать разложение интеграла.
interface
uses mathUnit;
type taskderivative=record
task:string;
answer:string;
end;
type tasklimits=record
task:string;
answer:string;
end;
function taskintegral1(var s:string):string;
function tasklimits1(var s:string):string;
function tasklimits2(var s:string):string;
function tasklimits3(var s:string):string;
function tasklimits4(var s:string):string;
function taskderivative1(var s:string):string;
function taskderivative2(var s:string):string;
procedure rand(var x:taskderivative);
procedure rand(var x:tasklimits);
implementation
function correct(s:string):string;
var i:integer;
begin
for i:=1 to length(s) do
case s[i] of
'{':s[i]:='(';
'}':s[i]:=')';
end;
result:=s;
end;
function tasklimits1(var s:string):string;
var
p1,p2:polynomialwithroot;
i:integer;
x:integer;
rez:string;
k1,k2,r1,r2:integer;
begin
randomize;
p1.roots(random(1,3));
p2.roots(random(1,3));
i:=random(p1.st)-1;
for i:=i downto 0 do
p2.root[random(p2.st)]:=p1.root[random(p1.st)];
i:=random(p1.st)+random(p2.st);
if(i>p1.st-1)then
begin
x:=p2.root[i-(p1.st-1)];
end
else
x:=p1.root[i];
p1.nw;
p2.nw;
rez:='Find:;lim_{xto!'+inttostr(x)+'}quad frac{'+p1.pltostr+'}{'+p2.pltostr+'}';
k1:=0;
k2:=0;
r1:=1;
r2:=1;
s:='При; сокращении;(x-'+inttostr(x)+'); получается;';
for i:=0 to p1.st-1 do
if(p1.kof[i]=x)then
inc(k1)
else
r1:=r1*(x-p1.kof[i]);
for i:=0 to p2.st-1 do
if(p2.kof[i]=x)then
inc(k2)
else
r2:=r2*(x-p2.kof[i]);
if(k1>k2)then
s:='0';// s:=s+'нуль';
if(k2>k1)then
s:='inf';//s:=s+'нуль; в; знаменателе; и; получается; бесконечность';
if(k1=k2)then
s:=inttostr(r1)+'/'+inttostr(r2);//s:=s+'число;'+floattostr(r1/r2);
s:=correct(s);
result:=rez;
end;
function tasklimits2(var s:string):string;
var
f:polynomialwithroot;
g,x:polynomial;
st:integer;
rez,answ:string;
begin
f.roots(random(1,2));
g.nw(random(1,2));
x.nw(random(1,2));
st:=f.root[random(0,f.st-1)];
rez:='Find:;lim_{xto!'+inttostr(st)+'}quad frac{'+(f*g).pltostr+'}{'+(f*x).pltostr+'}';
s:=floattostr(g.into(st))+'/'+floattostr(x.into(st));
s:=correct(s);
result:=rez;
end;
function tasklimits3(var s:string):string;
var
f,g:sqrnpolynomial;
x:polynomial;
rez,answ:string;
begin
f.nw(random(1,4),2);
g.nw(f.x.st,2);
x:=f.x-g.x;
rez:='Find:;lim_{xtoinfty}quad '+f.s+'-'+g.s;
if(x.st+1=f.x.st)then
s:=floattostr(x.kof[x.st])+'/'+floattostr(g.x.kof[g.x.st]+f.x.kof[g.x.st])
else
s:='0';
s:=correct(s);
result:=rez;
end;
function tasklimits4(var s:string):string;
var
f,g:polynomialwithroot;
kf1,kf2:polynomial;
a,i,j,num:integer;
rez,add:string;
begin
f.roots(random(1,2));
g.roots(random((f.st),3));
num:=random(1,f.st-1);
for i:=0 to num-1 do
g.root[i]:=f.root[i];
g.nw;
// writeln(num);
sleep(1000);
num:=0;
for i:=0 to f.st-1 do
for j:=0 to g.st-1 do
if(f.kof[i]=g.kof[j])then num+=1;
// writeln(num);
// sleep(1000);
kf1.nw(random(1,2));
kf2.nw(0);
a:=random(2,5);
add:='frac{'+(kf1+kf2).pltostr+'}{'+kf1.pltostr+'}';
for i:=1 to length(s) do
if(add[i]='x')then add[i]:='n';
rez:='Find ; x,; when: ;lim_{ntoinfty}quad '+
add+'frac{('+f.pltostr+')^{n^'+inttostr(a)+'}}{('+g.pltostr+')^{n^'+inttostr(a)+'}}=e^{'+floattostr(kf2.kof[0])+'}';
s:=inttostr(num);
result:=rez;
end;
function taskintegral1(var s:string):string;
var
tr1:sinx;
tr2:cosx;
tr3:tgx;
tr4:ctgx;
f,g:polynomial;
r:integer;
rez:string;
begin
rez:='Find;int ';
r:=random(1,5);
case r of
1:begin
tr1.x.nw(random(1,3));
tr1.nw;
s:=tr1.s;
tr1.derivative;
rez:=rez+tr1.s+';dx';
end;
2:begin
tr2.x.nw(random(1,3));
tr2.nw;
s:=tr2.s;
tr2.derivative;
rez:=rez+tr2.s+';dx';
end;
3:begin
tr3.x.nw(random(1,3));
tr3.nw;
s:=tr3.s;
tr3.derivative;
rez:=rez+tr3.s+';dx';
end;
4:begin
tr4.x.nw(random(1,3));
tr4.nw;
s:=tr4.s;
tr4.derivative;
rez:=rez+tr4.s+';dx';
end;
5:begin
r:=random(1,2);
f.nw(random(1,3));
rez:=rez+'('+f.pltostr+')';
while(r<>0)do
begin
g.nw(random(1,3));
f:=f*g;
rez:=rez+'('+g.pltostr+')';
r:=r-1;
end;
f.integral;
s:=correct(f.pltostr);
rez:=rez+';dx';
end;
end;
s:=correct(s);
result:=rez;
end;
function taskderivative1(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g:polynomial;
r:integer;
rez:string;
bg,answ:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find; frac{d}{dx};('+rez;
rez:=rez+')';
r:=random(1,2);
f.nw(random(1,3));
while(r>0)do
begin
g.nw(random(1,3));
rez:=rez+'(';
rez:=rez+g.pltostr;
rez:=rez+')';
f:=f*g;
r:=r-1;
end;
rez:=rez+')';
answ:='('+answ+')*('+g.pltostr+')+(';
g.derivative;
answ:=answ+bg+')*('+g.pltostr+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
function taskderivative2(var s:string):string;
var
sinx1,sinx2:sinx;
cosx1,cosx2:cosx;
tgx1,tgx2:tgx;
ctgx1,ctgx2:ctgx;
f,g,st:polynomial;
r:integer;
rez:string;
answ,bg:string;
begin
randomize;
sinx1.x.nw(random(1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw(random(1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw(random(1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw(random(1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random(1,4);
case r of
1:begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2:begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3:begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos('+tgx1.x.pltostr+')^2)';
end;
4:begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find; frac{d}{dx};('+rez;
rez:=rez+')^{';
f.nw(random(1,3));
rez:=rez+f.pltostr+'}';
st:=f;
st.derivative;
answ:='(('+bg+')^{'+f.pltostr+'})*(('+st.pltostr+')*ln('+bg+')+('+f.pltostr+')*('+answ+')/('+bg+')';
s:=answ;
s:=correct(s);
result:=rez;
end;
procedure rand(var x:taskderivative);
var
r:integer;
begin
randomize;
r:=random(1,2);
case r of
1:x.task:=taskderivative1(x.answer);
2:x.task:=taskderivative2(x.answer);
end;
end;
procedure rand(var x:tasklimits);
var
r:integer;
begin
randomize;
r:=random(1,4);
case r of
1:x.task:=tasklimits1(x.answer);
2:x.task:=tasklimits2(x.answer);
3:x.task:=tasklimits3(x.answer);
4:x.task:=tasklimits4(x.answer);
end;
end;
end.
Суммируя
Существует большое разнообразие типовых приемов и примеров, но для минимальной оценки понимания материала такой набор меня пару раз выручил. Разумеется этот набор можно расширять и расширять, но это дело каждого.
Ссылка на программу: GitHub
В том проекте есть и другие задачи, не описанные в этой статье по причине их неоднозначной работы (тестируются и обновляются).
Автор: Gr13