В этой статье я хочу познакомить вас с популярным инструментом для оценки финансового риска VaR (ValueAtRisk). При этом я постараюсь использовать минимум экономических, математических и статистических терминов.
Главные идеи VaR были разработаны и применены в банке JP Morgan в 80-х. Широкое применение VaR получил в 1993 когда был одобрен Группой тридцати(G-30) как часть “лучших практик” для работы с деривативами(производными финансовыми инструментами). А позже стала одним из показателей риска банка по системе Базель II (набор международных рекомендации по банковскому регулированию). Идею используемую в VaR можно отследить до ранних работ лауреата нобелевской премии по экономике Гарии Марковица в 1952.
Зачем нужен VaR?
VaR имеет много применений:
- банки определяют текущий риск по отделам и банку вообщем;
- трейдеры используют VaR в торговых стратегиях (например для определения момента выхода из сделки);
- частные инвесторы для выбора менее рискованных вложений;
Управление рисками
Сначала давайте разберемся что такое управление рисками и зачем это надо.
“Управление рисками это процесс обнаружения, анализа и принятия или смягчения неопределенности в инвестиционных решениях. В сущности, управление рисками происходит всегда когда инвестор или управляющий фондом анализирует и пытается оценить потенциальные убытки и затем принять(или не принять) необходимые меры, учитывая его инвестиционные цели и толерантность к риску”.
→ Источник
Почему управление рисками актуально? Даниел Канеман в своей книге “Думай медленно… решай быстро” утверждает, что люди не любят проигрывать больше чем любят выигрывать. То есть, если человеку предлагают с 50% выиграть 110$ и с 50% проиграть 100$, то он скорее всего откажется, хотя потенциальный выигрыш и больше. Автор называет это ассиметрией потерь (loss averse).
Прогнозированием возможных потерь, к которым люди так чувствительны, мы с вами и займемся. Но перед тем как переходить к VaR нам нужно поговорить о понятии волатильности, без которой невозможно представить управление рисками.
Немного о Волатильности
Сначала рассмотрим два примера.
Пример 1 — пусть весь прошлый года акция А каждый день либо росла на 3%, либо теряла -1%. При этом эти два события были независимы и равновероятны. Если наши вложения составляют 100$, то мы можем с высокой вероятностью сказать, что завтра тенденция сохранится и мы либо получим 3$, либо потеряем -1$ с одинаковой вероятностью. Другими словами вероятность получить +3$ равна 50% и вероятность потерять -1$ тоже равна 50%. Мы даже можем сказать, что ожидаемая прибыль каждый день равна 1$ (3$*50%-1$*50%). Но как мы увидим позже, ожидаемая прибыль это не то что нас интересует при управлении рисками. Для нас важны именно убытки, и с возможными убытками здесь все ясно — с вероятностью 50% мы можем потерять затра $1.
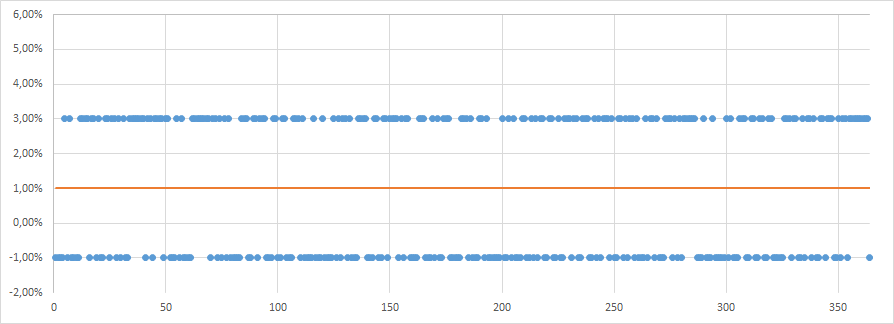
Случайный доход +3% или -1%
Теперь давайте рассмотрим пример 2. Есть информация о ежедневном доходе акции В за прошлый год. Свойства дохода:
- принимал одно из четырех значение -4%, -3%, +5%, +6%;
- вероятность каждого из четырех событий одинаковая — 25%;
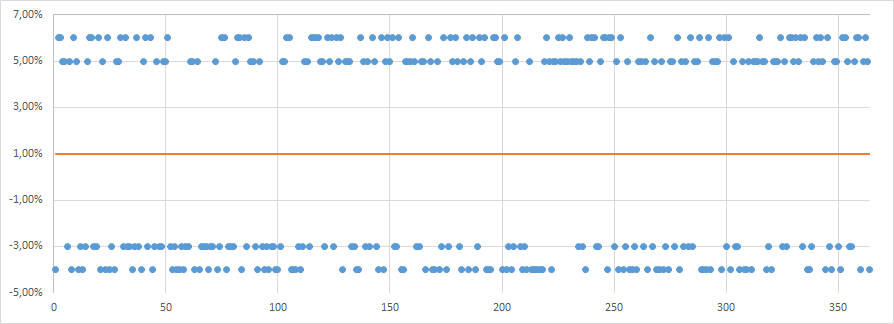
Случайный доход -3%, -4%, 5% или 6%
Я специально подобрал значения так, чтобы среднее значение было +1%(-4%*25% -3%*25% +5%*25% +6%*25%) как и в первом примере. То есть, если у нас есть акции на 100$, то ожидаемое значение завтра тоже будет 1$.
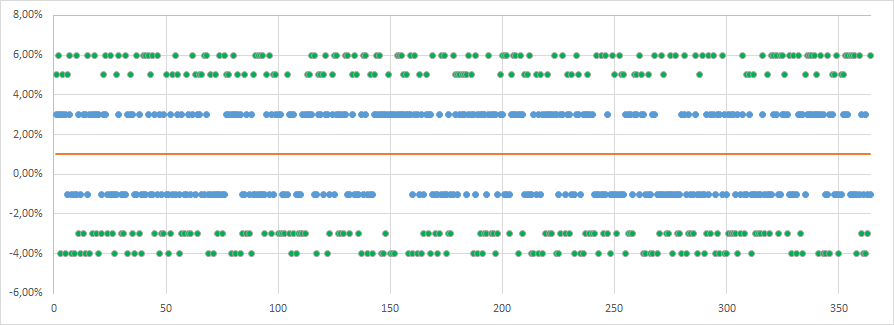
Сравнение примера 1(-1%, +3%) и примера 2(-3%, -4%, 5%, 6%)
Хотя ожидаемые значения в двух случаях одинаковы (+1%), уровень риска разный, так как размер убытков может быть выше во втором случае. Это и есть волатильность.
Волатильность, изменчивость (англ. volatility) — статистический финансовый показатель, характеризующий изменчивость цены. Является важнейшим финансовым показателем и понятием в управлении финансовыми рисками, где представляет собой меру риска использования финансового инструмента за заданный промежуток времени.
Или своими словами, волатильность — это сила разброса значений. Чем больше разброс, тем выше волатильность и тем труднее нам делать предположение о цене в будущем. Напрашивается вывод, чем выше волатильность, тем выше риск. Казалось бы, что волатильность это тот показатель, который нам нужен.
Но у волатильности есть один существенный недостаток для управления рисками. Она учитывает как разброс прибылей так и разброс убытков. Например, если цена на акцию резко вырастет, то и волатильность увеличится. Хотя риск, с точки зрения возможных потерь, останется на том же уровне. Эту проблему решит VaR, но перед тем как переходить к VaR давайте разберемся с проблемой оценки убытков.
Проблема 1. Как описать потенциальные убытки?
Если в первом примере прогноз убытков на завтра был -1% с вероятностью 50%, то во втором ситуация сложнее. Мы можем сказать что:
- с вероятностью 25% мы потеряем 3%;
- с вероятностью 25% мы потеряем 4%;
- c вероятностью 50% мы потеряем более 3%;
Все эти утверждения верны, а ведь у нас только 4 возможных исхода. В реальной жизни количество исходов может быть намного больше. Соответственно увеличится и количество утверждений, которые мы можем сделать о вероятности риска. А это усложняет донесение и анализ информации.
Проблема 2. Экстремальные значения.
Давайте представим, что прошлый год акция принимала значения от -5% до 5%, но в один день убыток был -10%. Если взять количество дней в году за 364 (для простоты забудем о выходных и праздниках), то вероятность повторения убытка в -10% равна 1/364=0.274%. Вероятность 0.274% довольно мала, ее трудно представить, а кто-то может посчитать ее вообще не существенной для рассмотрения. Как быть в этом случае?
В обоих этих случаях к нам на помощь и приходит VaR.
VaR
VaR позволяет оценить убытки с определенной вероятностью. И сделать это можно довольно кратко, чтобы человек мог относительно легко представить размер риска. VaR отвечает на следующий вопрос:
“Какой максимальный убыток я могу ожидать в течение определенного отрезка времени с заданным уровнем вероятности(доверия)”
Например, VaR 100$ c порогом 99% значит:
- с вероятностью 1% мы можем потерять 100$ и более в течении дня;
- с вероятностью 99% мы не потеряем более 100$ в течении дня;
Оба этих высказывания эквивалентны.
VaR состоит из трех компонентов:
- уровень/порог прогноза (обычно 95% или 99%);
- временной интервал прогноза (день, месяц или год);
- возможные потери (количество денег (обычно долларов) или процентах);
Возможность выбрать порог (99% в нашем примере) является очень удобным свойством для многих инвесторов. Это свойство позволяет приблизится к ответу на вопрос, который волнует многих инвесторов “сколько мы можем потерять в течение дня (месяца) в худшем случае?”.
Существует три метода получения VaR: исторический, ковариационный и метод Монте-Карло.
В этой статье мы рассмотрим исторический метод, так как он требует наименьших знаний в области статистики и, по-моему, самый интуитивный из трех.
Шаги подсчета VaR:
- Собрать исторические данные о доходе за определенный период (месяц, год);
- Отсортировать данные по возрастанию;
- Выбрать порог с которым мы хотим делать прогноз и “отрезать” наихудшее значение зная порог;
Для большей наглядности давайте выполним этот процесс нахождения VaR для реального примера. В качестве примера мы рассмотрим цены на акции Apple в 2015 году.
Шаги:
1. Получить данные о доходности акций в процентах. Скачать данные можно например с yahoo.finance.com. Yahoo предоставляет цены открытия, закрытия и тд. Мы рассмотрим цены закрытия(close*). Обратите внимания что на yahoo даты отсортированы в порядке убывания, так что можно отсортировать в порядке возрастания. Мы преобразуем цены закрытия в прибыль в процентах с предыдущего дня. Например, если цена вчера была 10$, а сегодня 15$, то прибыль в процентах будет (15$-10$)/10$ = 50%;
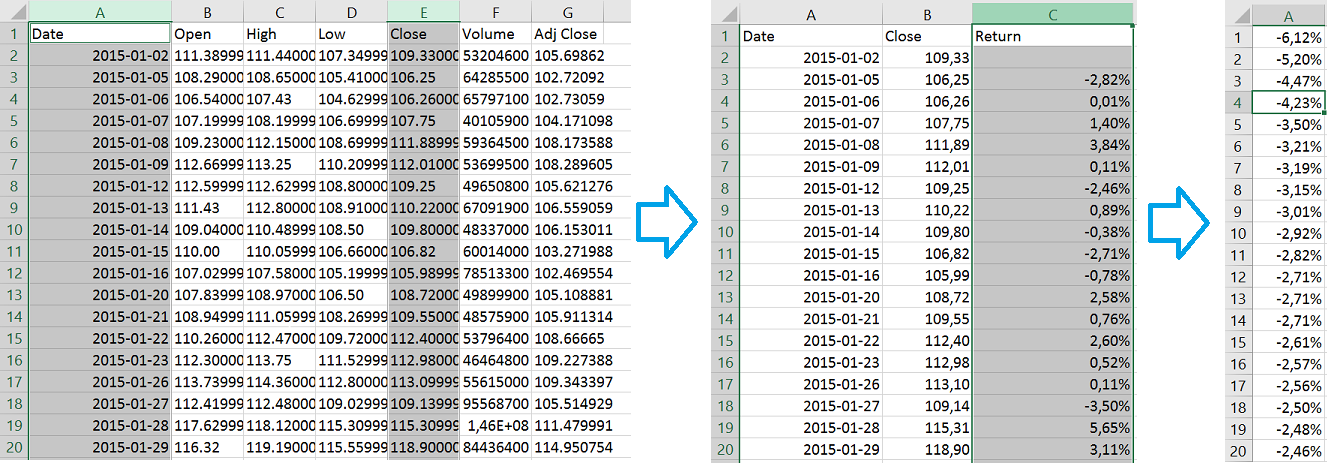Преобразование данных из Yahoo и сортировка
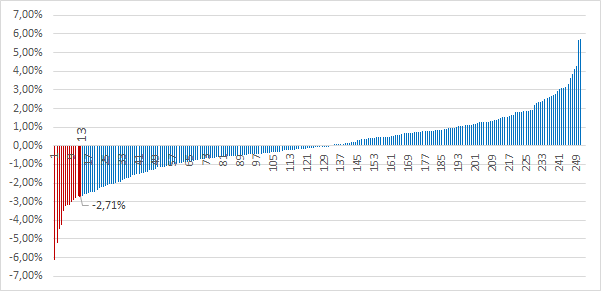
2. Отсортировать прибыли по возрастанию (для наглядности я построил гистограмму);
3. Выбрать порог, с которым мы хотим делать прогноз, и “отрезать” наихудшее значение зная порог. У нас 252 рабочих дня. Если мы хотим сделать оценку покрывающую 95% случаев, то мы отбрасываем худшие 5%, вероятность которых мы считаем низкой. 5% от 252 дней это 13 дней (округляем 12.6 до 13). Если посмотреть на график, то видно, что доход 13-ого “худшего деня” был -2.71%. Теперь мы можем сказать что с вероятностью 95% мы не потеряем более 2.71%. Если наши вложения 100$, то с вероятностью 95% мы не потеряем более 2,71$. Это не значит, что мы не можем потерять более 2,71$, мы говорим о вероятности в 95%. Если этого недостаточно, то можно увеличить порог например до 99%;
* Мы выбираем close цену, а не adj. close, так как adj. close непостоянна и может меняться со временем. Например, если происходят split-ы акций. Наша же цель, чтобы цифры сошлись у тех, кто выполнит этот пример позже.
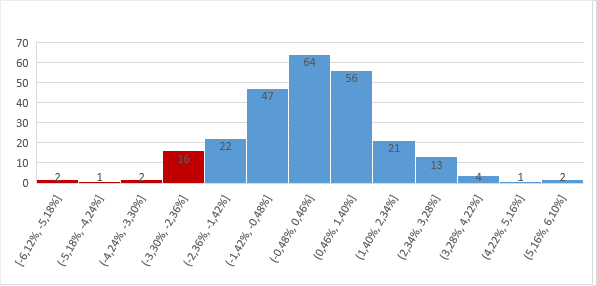Завершая пример с данными Apple, привожу еще один интересный график. На графике по горизонтали мы видим диапазоны прибылей, и по вертикале — количество дней, когда прибыль попадала в соответствующий интервал. Этот график очень похож на нормальное распределение. Этот факт нам пригодится в следующие статье где мы рассмотрим два других метода подсчета VaR.
public Double calculateHistoricalVar(List<Double> prices, Double confidenceLevel, Double amount) {
if (prices.isEmpty()) {
return 0d;
}
List<Double> returns = getReturns(prices);
Collections.sort(returns);
double threshold = (returns.size() * (1 - confidenceLevel));
int intPart = (int) threshold;
Double decimalPart = threshold - intPart;
Double rawVar = returns.get(intPart);
Double interpolatedPart = decimalPart * (returns.get(intPart) - (returns.get(intPart + 1)));
return rawVar + interpolatedPart;
}
private List<Double> getReturns(List<Double> prices) {
List<Double> result = new ArrayList<>(prices.size());
for (int i = 1; i < prices.size(); i++) {
result.add(prices.get(i) / (prices.get(i - 1)) - 1);
}
return result;
}Немного о недостатках исторического метода и VaR вообщем:
- Мы прогнозируем будущие, используя исторические данные. Это может быть хрупким предположение. Так как мы делаем предположение, что события из прошлого будут повторяться. Можно пытаться бороться с этим используя разные временные интервалы для подсчета VaR(год, месяц, день). Об этом мы поговорим ниже.
- VaR ничего не говорит, о значениях за пределами порога, например 95%. Мы можем иметь две разных акции А и B с VaR 50$ при пороге 95% и 100 наблюдениях. Пусть 95 лучших наблюдений у А и В одинаковы и равны от -50$ до 45$ с шагом 1$. Но пять худших прибылей А = {-1000$, -800$, -700$, -600$, -500$}, а В = {-100$, -99$, -98$, -97$, -96$}. Очевидно что риск для B выше. Можно пробовать бороться с этим увеличивая порог(до 99%, 99.9%, 99.99% и тд.). Также существуют методы, специально направленные на устранения этих недостатков, например, Conditional VAR, который оценивает убытки, если потери превысили VaR. Но мы не будем рассматривать их в этой статье.
Вопросы которые могут возникнуть при работе с VaR:
- Как выбрать период?
- На это нет определенного ответа, все зависит от вашего инвестиционного горизонта. Банки обычно считают VaR для дней, пенсионные фонды, с другой стороны, часто считают VaR для месяцев.
- Что делать если 95% это не целый номер элемента?
- В нашем примере мы использовали 252 дня и порог 95%. Элемент, который мы отсекаем равняется 252*0.05=12.6. В нашем примере мы просто округли и взяли 13-ый элемент, но если быть точными, то наше значение должно быть где-то посередине. К сожалению, в нашем примере 12-ый и 13-ый элементы равны -2.71%. Поэтому, давайте представим, что 12-ый элементы равен -4%, а 13-ый -3%. Тогда VaR будет находится между -4% и -3%, ближе к -3%. А точнее -3.6%. Здесь к нам на помощь и приходит интерполяция. Формула выглядит так:
b+(a-b)*k , где а-нижнее значение, b-верхнее значение и k-дробная часть (в нашем случае 0.6)
Получается -3% + (-4% + 3%) * 0.6 = -3.6%
Заключение
Красота подхода VaR в том, что он отлично работает и для набора из нескольких акций или комбинации разных ценных бумаг. Например, VaR для набора из облигаций и валют дает нам оценку без особых усилий. А использование других способов, таких как анализ возможных сценариев, сильно усложняется из-за корреляции (связи) между ценными бумагами.
→ Источник
Автор: AlexeyPi
