В дополнение к опубликованной ранее Методике управления рисками я хотел бы поделиться с уважаемыми коллегами описанием алгоритма построения графика распределения вероятности достижения тех или иных значений измеряемых величин в процессе управления проектом. Данный алгоритм отчасти основан на работе Т. ДеМарко, описанной в его книге «Вальсируя с медведями», однако в целом использует некоторые упрощения, которые предлагаются вероятностным подходом и линейной интерполяцией.
1. Общие сведения
Алгоритм построения графика распределения вероятности для объектов воздействия рисков может использоваться руководителями проектов для оценки вероятности достижения тех или иных значений таких измеримых показателей проекта, как срок или бюджет, при выполнении проекта в условиях наличия рисков. Данный алгоритм применяется при первоначальном составлении реестра рисков, а также при каждом изменении параметров тех рисков, которые влияют на распределение вероятности значений измеримых параметров.
Для применения алгоритма необходимо иметь базовые знания теории вероятности (в объёме формулы вычисления общей вероятности нескольких независимых событий).
2. Входные данные
Входными данными для алгоритма являются:
- Целевые значения измеримых показателей (например, срок сдачи проекта, допустимый бюджет проекта и т. д.).
- Реестр рисков проекта, как можно более полный и непротиворечивый.
Все риски по одному и тому же объекту воздействия должны быть разделены на два больших класса: свершившиеся (то есть уже проблемы) и пока ещё отслеживаемые (то есть пока всё ещё риски). Для пока ещё рисков необходимо получить чёткую количественную оценку для вероятности риска и воздействия риска. Для качественной оценки вероятности можно воспользоваться следующим классификатором:
- Низкая — 25 %.
- Средняя — 50 %.
- Высокая — 75 %.
Однако руководитель проекта самостоятельно может делать оценки качественных значений вероятности, основанные на условиях исполнения конкретного проекта и других факторов. При этом необходимо всегда следовать правилу, что количественное представление значения вероятности «Низкая» не может превышать представление для значения «Средняя», а второе не может превышать значение «Высокая».
Для количественной оценки параметра «Степень воздействия» руководитель проекта должен пользоваться своими собственными эвристиками. Например, для объекта воздействия «Сроки проекта» такой эвристикой может быть следующий классификатор:
- Низкая — от 3 до 7 календарных дней.
- Средняя — от 7 до 30 календарных дней.
- Высокая — более 30 календарных дней.
Опять же надо следовать указанному выше правилу касательно относительных значений.
3. Упрощённая схема расчёта
Упрощённая схема расчёта применяется для очень быстрой и достаточно неточной оценки того, как могут повлиять текущие проблемы и риски на измеримые объекты воздействия. При помощи этой схемы расчёт можно сделать очень быстро, однако его придётся уточнять при помощи детального расчёта.
Пусть G — целевое значение некоторого измеримого объекта воздействия, который существует в условиях наличия рисков, на него воздействующих. В этом случае необходимо выполнить следующие расчёты:
- Сложить все количественные значения степени воздействия для проблем (рисков со 100 % вероятности). Пусть полученная сумма обозначается как I.
- Перемножить количественные значения степеней воздействия для рисков на количественные значения вероятностей этих рисков, после чего полученные значения сложить. Пусть полученная сумма обозначается как R.
- Значение (G + I) и ниже соответствует вероятности достижения 0 %.
- Значение (G + I + R) и выше соответствует вероятности достижения 100 %.
- Вероятность промежуточных значений вычисляется посредством линейной интерполяции.
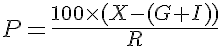
где X — промежуточное значение измеримого объекта воздействия.
В разделе 5 приводится пример проведения расчётов.
4. Детальный расчёт
Детальный расчёт позволяет более точно оценить вероятность достижения тех или иных значений измеримого объекта воздействия рисков. Данный алгоритм основан на вероятностном подходе и позволяет ответить на вопросы вроде: «С какой вероятностью срок сдачи проекта не превысит запланированный более чем на 20 %?», «С какой вероятностью проект будет выполнен с превышением бюджета не более чем на 50 %?» и т. д.
Опять же, пусть G — целевое значение измеримого объекта воздействия, который существует в условиях наличия рисков, на него воздействующих. В этом случае необходимо выполнить следующие расчёты:
- Сложить все количественные значения степени воздействия для проблем (рисков со 100 % вероятности). Пусть полученная сумма обозначается как I.
- Для всех рисков построить таблицу с двоичными значениями, где значение «0» обозначает, что соответствующий риск не проявился, а значение «1» обозначает, что соответствующий риск проявился. Количество строк в такой таблице будет равно 2N, где N — количество рисков.
- Для каждой строки таблицы необходимо рассчитать вероятность осуществления именно такой комбинации проявлений и непроявлений рисков. Данная вероятность считается как произведение вероятностей проявления рисков (Pi) и непроявлений рисков (1 — Pi). Для данной вероятности рассчитывается слагаемое к измеримому значению объекта воздействия в виде суммы количественных оценок воздействий для тех рисков, которые проявляются в данной строке.
- Для всего списка слагаемых к измеримому значению объекта воздействия окончательно рассчитываются вероятности путём сложения всех рассчитанных ранее вероятностей, если несколько вероятностей соответствуют одному и тому же рассчитанному слагаемому. В итоге должно получиться множество слагаемых, в котором каждое значение содержится ровно один раз, а сумма вероятностей равна 100 %.
- Полученное на предыдущем шаге множество необходимо отсортировать, на основании отсортированного множества строится шкала от (G + I) + X1 до (G + I) + XM, а для каждого значения на этой шкале вероятность рассчитывается нарастающим итогом. Это значит, что для значения (G + I) + XM вероятность будет составлять 100 %. Эта вероятность показывает достижение соответствующего значения измеримого объекта воздействия (до или точно). То есть с вероятностью 100 % измеримый объект воздействия будет иметь значение (G + I) + XM или ниже.
- Вероятности промежуточных значений, не входящих в построенное ранее упорядоченное множество рассчитываются всё так же посредством линейной интерполяции.
- По рассчитанным вероятностям можно построить график для наглядного представления полученного распределения вероятности.
В разделе 5 приводится пример проведения расчётов.
5. Пример применения алгоритма
Пусть для некоторого проекта имеются следующие выявленные риски:
| Код | Объект воздействия | Вероятность | Степень воздействия |
| R01 | Сроки проекта | Осуществлён | Средняя |
| R02 | Сроки проекта | Высокая | Низкая |
| R03 | Сроки проекта | Средняя | Средняя |
| R04 | Сроки проекта | Низкая | Высокая |
| R05 | Бюджет проекта | Средняя | Средняя |
По текущим планам проект должен быть завершён 01.05.2012, его бюджет составляет 100 тысяч рублей.
Расчёт будет производиться для сроков проекта (выделенный для примера объект воздействия; в реальной практике такой расчёт должен производиться для всех измеримых объектов воздействия). Это значит, что в расчёте участвуют только риски R01, R02, R03 и R04. Пусть руководитель проектов сопоставил этим рискам следующие количественные значения вероятности и степени воздействия:
| Код | Вероятность | Степень воздействия |
| R01 | 100 % | 10 дней |
| R02 | 75 % | 5 дней |
| R03 | 50 % | 7 дней |
| R04 | 25 % | 14 дней |
Поскольку риск R01 проявился, то к плановой дате завершения проекта необходимо прибавить 10 календарных дней. Таким образом, нулевая вероятность исполнения соответствует 11.05.2012.
Упрощённый расчёт предполагает, что остальные риски дадут прирост в: 5 * 75 % + 7 * 50 % + 14 * 25 %, что даёт результат 10.75, то есть приблизительно 11 календарных дней. Это значит, что стопроцентная вероятность соответствует 22.05.2012.
Визуализация полученных данных представлена на следующем графике:
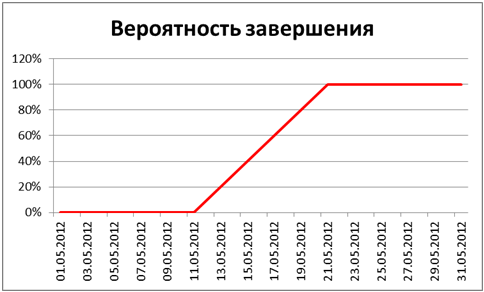
При проведении детального расчёта для рисков необходимо составить следующую таблицу:
| R02 | R03 | R04 | Вероятность | Воздействие |
| 0 | 0 | 0 | 9,38 % | 0 |
| 0 | 0 | 1 | 3,13 % | 14 |
| 0 | 1 | 0 | 9,38 % | 7 |
| 0 | 1 | 1 | 3,13 % | 21 |
| 1 | 0 | 0 | 28,13 % | 5 |
| 1 | 0 | 1 | 9,38 % | 19 |
| 1 | 1 | 0 | 28,13 % | 12 |
| 1 | 1 | 1 | 9,38 % | 26 |
Данная таблица преобразуется в следующую шкалу для построения распределения вероятности:
| Воздействие | 0 | 5 | 7 | 12 | 14 | 19 | 21 | 26 |
| Вероятность | 9,38 % | 28,13 % | 9,38 % | 28,13 % | 3,13 % | 9,38 % | 3,13 % | 9,38 % |
| Нарастающим | 9,38 % | 37,50 % | 46,88 % | 75,00 % | 78,13 % | 87,50 % | 90,63 % | 100,00 % |
| Дата | 11.05.12 | 16.05.12 | 18.05.12 | 23.05.12 | 25.05.12 | 30.05.12 | 01.06.12 | 06.06.12 |
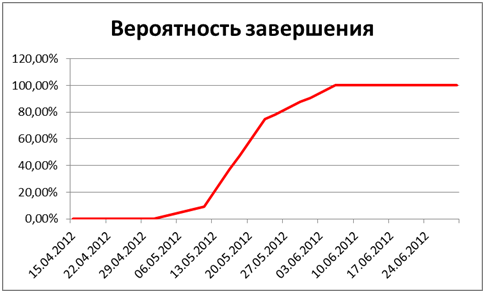
Значения в этой таблице интерпретируются следующим образом: «С вероятностью 75 % проект будет завершён не позднее 23.05.2012 (или ранее), если никаких других негативных воздействий на сроки проекта оказано не будет».
Визуализация полученных данных представлена на следующем графике:
Всех читателей благодарю за силы и время, потраченные на эту статью. Ну а за конструктивные комментарии с предложениями, замечаниями и критикой как всегда низкий поклон.
Если вы хотите дополнительно отблагодарить автора, но не знаете как, то вам сюда.
Мои предыдущие статьи по теме управления проектами на Хаброхабре:
- Методика управления рисками — обобщение моего опыта работы над проектами
- Апробация методики управления рисками: пять главных национальных рисков России
Автор: Darkus