Всё, что вы хотели знать о динамическом программировании, но боялись спросить
Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.
# Весь код в статье написан на языке Python
Основы
Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.
Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.
Порядок пересчёта
Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.
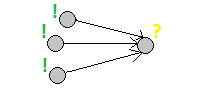
2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.
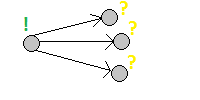
3) Ленивая динамика:
Рекурсивная мемоизированная [1] функция пересчёта динамики. Это что-то вроде поиска в глубину [2] по ацикличному графу состояний, где рёбра — это зависимости между ними.
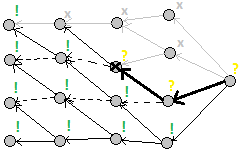
Элементарный пример: числа Фибоначчи [3]. Состояние — номер числа.
Прямой порядок:
fib[1] = 1 # Начальные значения
fib[2] = 1 # Начальные значения
for i in range(3, n + 1):
fib[i] = fib[i - 1] + fib[i - 2] # Пересчёт состояния i
Обратный порядок:
fib[1] = 1 # Начальные значения
for i in range(1, n):
fib[i + 1] += fib[i] # Обновление состояния i + 1
fib[i + 2] += fib[i] # Обновление состояния i + 2
Ленивая динамика:
def get_fib(i):
if (i <= 2): # Начальные значения
return 1
if (fib[i] != -1): # Ленивость
return fib[i]
fib[i] = get_fib(i - 1) + get_fib(i - 2) # Пересчёт
return fib[i]
Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.
Многомерная динамика
Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.
Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:
Пример №1: Количество СМСок
Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:
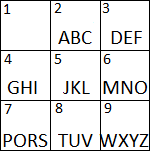
Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.
dp[n][m] — количество различных сообщений длины n, использующих m нажатий.2) Начальное состояние: Есть одно сообщение длины ноль, использующее ноль нажатий — пустое.
3) Формулы пересчёта: есть по восемь букв, использующих одно, два и три нажатия соответственно, а так же две буквы за 4 нажатия.
Прямой пересчёт:
dp[n][m] = (dp[n - 1][m - 1] + dp[n - 1][m - 2] + dp[n - 1][m - 3]) * 8 + dp[n - 1][m - 4] * 2
Обратный пересчёт:
dp[n + 1][m + 1] += dp[n][m] * 8
dp[n + 1][m + 2] += dp[n][m] * 8
dp[n + 1][m + 3] += dp[n][m] * 8
dp[n + 1][m + 4] += dp[n][m] * 2
4) Порядок пересчёта:
Если писать прямым методом, то надо отдельно подумать о выходе за границу динамики, к примеру, когда мы обращаемся к dp[n - 1][m - 4], которого может не существовать при малых m. Для обхода этого можно или ставить проверки в пересчёте или записать туда нейтральные элементы (не изменяющие ответа).
При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.
5) Ответ — это сумма всех состояний.
Пример №2: Конь
Шахматный конь стоит в клетке (1, 1) на доске размера N x M. Требуется подсчитать количество способов добраться до клетки (N, M) передвигаясь четырьмя типами шагов:
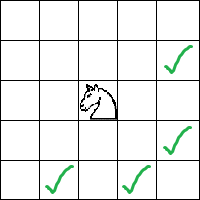
dp[i][j] — количество способов добраться до (i, j).2) Начальное значение: В клетку
(1, 1) можно добраться одним способом — ничего не делать.3) Формула пересчёта:
Для прямого порядка:
dp[i][j] = dp[i - 2][j - 1] + dp[i - 2][j + 1] + dp[i - 1][j - 2] + dp[i + 1][j - 2]
Для обратного порядка:
dp[i + 1][j + 2] += dp[i][j]
dp[i + 2][j + 1] += dp[i][j]
dp[i - 1][j + 2] += dp[i][j]
dp[i + 2][j - 1] += dp[i][j]
4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.
Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.
Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход на подобии такого:
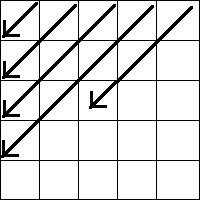
Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.
5) Ответ просто лежит в dp[n][m].
Динамика и матрица переходов
Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы вики [4].
Допустим, есть задача, которую мы уже решили динамическим программированием, например, извечные числа Фибоначчи.
Давайте немного переформулируем её. Пусть у нас есть вектор 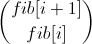 , из которого мы хотим получить вектор
, из которого мы хотим получить вектор 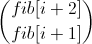 . Чуть-чуть раскроем формулы:
. Чуть-чуть раскроем формулы: 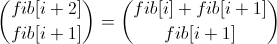 . Можно заметить, что из вектора
. Можно заметить, что из вектора 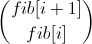 можно получить вектор
можно получить вектор 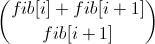 путем умножения на какую-то матрицу, ведь в итоговом векторе фигурируют только сложенные переменные из первого вектора. Эту матрицу легко вывести, вот она:
путем умножения на какую-то матрицу, ведь в итоговом векторе фигурируют только сложенные переменные из первого вектора. Эту матрицу легко вывести, вот она: 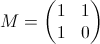 . Назовём её матрицей перехода.
. Назовём её матрицей перехода.
Это значит, что если взять вектор 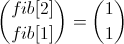 и умножить его на матрицу перехода
и умножить его на матрицу перехода n - 1 раз, то получим вектор 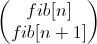 , в котором лежит
, в котором лежит fib[n] — ответ на задачу.
А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть 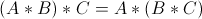 (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так:
(но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: 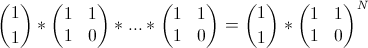 .
.
Это хорошо тем, что теперь можно применить метод быстрого возведения в степень [5], который работает за 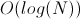 . Итого мы сумели посчитать
. Итого мы сумели посчитать N-ое число Фибоначчи за логарифм арифметических операций.
А теперь пример посерьёзнее:
Пример №3: Пилообразная последовательность
Обозначим пилообразную последовательность длины N как последовательность, у которой для каждого не крайнего элемента выполняется условие: он или меньше обоих своих соседей или больше. Требуется посчитать количество пилообразных последовательностей из цифр длины N. Выглядит это как-то так:
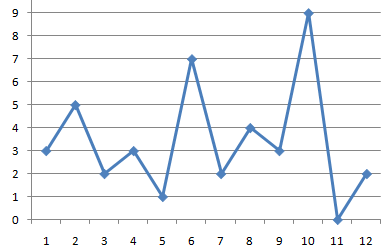
1) Состояние динамики: dp[n][last][less] — количество пилообразных последовательностей длины n, заканчивающихся на цифру last. Причём если less == 0, то последняя цифра меньше предпоследней, а если less == 1, значит больше.
2) Начальные значения:
for last in range(10):
dp[2][last][0] = 9 - last
dp[2][last][1] = last
3) Пересчёт динамики:
for prev in range(10):
if prev > last:
dp[n][last][0] += dp[n - 1][prev][1]
if prev < last:
dp[n][last][1] += dp[n - 1][pref][0]
4) Порядок пересчёта: мы всегда обращаемся к предыдущей длине, так что просто пара вложенных for'ов.
5) Ответ — это сумма dp[N][0..9][0..1].
Теперь надо придумать начальный вектор и матрицу перехода к нему. Вектор, кажется, придумывается быстро: все состояния, обозначающие длину последовательности N. Ну а матрица перехода выводится, смотря на формулы пересчёта.

Динамика по подотрезкам
Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.
Пример №4: Запаковка строки
Вот Развернутое условие [6]. Я вкратце его перескажу:
Определим сжатую строку:
1) Стока состоящая только из букв — это сжатая стока. Разжимается она в саму себя.
2) Строка, являющаяся конкатенацией двух сжатых строк A и B. Разжимается она в конкатенацию разжатых строк A и B.
3) Строка D(X), где D — целое число, большее 1, а X — сжатая строка. Разжимается она в конкатенацию D строк, разжатых из X.
Пример: “3(2(A)2(B))C” разжимается в “AABBAABBAABBC”.
Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.
1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.
dp_len = r - l
dp[l][r] = dp_len # Первый вариант сжатия - просто строка.
for i in range(l + 1, r):
dp[l][r] = min(dp[l][r], dp[l][i] + dp[i][r]) # Попробовать разделить на две сжатые подстроки
for cnt in range(2, dp_len):
if (dp_len % cnt == 0): # Если не делится, то нет смысла пытаться разделить
good = True
for j in range(1, (dp_len / cnt) + 1): # Проверка на то, что все cnt подстрок одинаковы
good &= s[l:l + dp_len / cnt] == s[l + (dp_len / cnt) * j:l + (self_len / cnt) * (j + 1)]
if good: # Попробовать разделить на cnt одинаковых подстрок и сжать
dp[l][r] = min(dp[l][r], len(str(cnt)) + 1 + dp[l][l + dp_len / cnt] + 1)
4) Порядок пересчёта: прямой по возрастанию длины подстроки или ленивая динамика.
5) Ответ лежит в d[0][len(s)].
Пример №5: Дубы [7]
Динамика по поддеревьям
Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.
Пример №6: Логическое дерево
Дано подвешенное дерево, в листьях которого записаны однобитовые числа — 0 или 1. Во всех внутренних вершинах так же записаны числа, но по следующему правилу: для каждой вершины выбрана одна из логических операций: «И» или «ИЛИ». Если это «И», то значение вершины — это логическое «И» от значений всех её детей. Если же «ИЛИ», то значение вершины — это логическое «ИЛИ» от значений всех её детей.
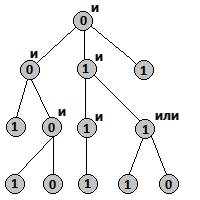
Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.
d[v][x] — количество операций, требуемых для получения значения x в вершине v. Если это невозможно, то значение состояния — +inf.2) Начальные значения: для листьев, очевидно, что своё значение можно получить за ноль изменений, изменить же значение невозможно, то есть возможно, но только за
+inf операций.3) Формула пересчёта:
Если в этой вершине уже значение
x, то ноль. Если нет, то есть два варианта: изменить в текущей вершине операцию или нет. Для обоих нужно найти оптимальный вариант и выбрать наилучший.
Если операция «И» и нужно получить «0», то ответ это минимум из значений d[i][0], где i — сын v.
Если операция «И» и нужно получить «1», то ответ это сумма всех значений d[i][1], где i — сын v.
Если операция «ИЛИ» и нужно получить «0», то ответ это сумма всех значений d[i][0], где i — сын v.
Если операция «ИЛИ» и нужно получить «1», то ответ это минимум из значений d[i][1], где i — сын v.
4) Порядок пересчёта: легче всего реализуется лениво — в виде поиска в глубину из корня.
5) Ответ — d[root][value[root] xor 1].
Динамика по подмножествам
В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.
Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера
Задан взвешенный (веса рёбер неотрицательны) граф G размера N. Найти гамильтонов цикл [8] (цикл, проходящий по всем вершинам без самопересечений) минимального веса.
0.
1) Состояние динамики: dp[mask][v] — путь минимального веса из вершины 0 в вершину v, проходящий по всем вершинам, лежащим в mask и только по ним.
2) Начальные значения: dp[1][0] = 0, все остальные состояния изначально — +inf.
3) Формула пересчёта: Если i-й бит в mask равен 1 и есть ребро из i в v, то:
dp[mask][v] = min(dp[mask][v], dp[mask - (1 << i)][i] + w[i][v])
Где w[i][v] — вес ребра из i в v.
4) Порядок пересчёта: самый простой и удобный способ — это написать ленивую динамику, но можно поизвращаться и написать перебор масок в порядке увеличения количества единичных битов в ней.
5) Ответ лежит в d[(1 << N) - 1][0].
Динамика по профилю
Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.
Эти задачи можно решить полным перебором за 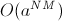 , где
, где a — количество вариантов замощения одной клетки. Динамика по профилю же оптимизирует время по одной из размерностей до линейной, оставив от себя в экспоненте только коэффициент. Получится что-то такое: 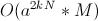 .
.
Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.
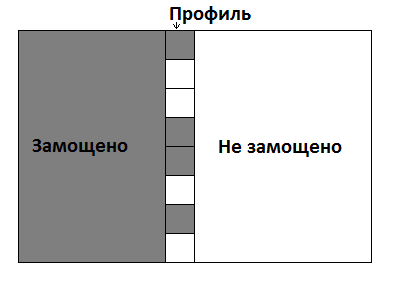
Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.
Пример №8: Замощение доминошками
Найти количество способов замостить таблицу N x M с помощью доминошек размерами 1 x 2 и 2 x 1.
0 — не замощенная клетка столбца, 1 — замощенная. То есть всего профилей 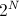 .
.
0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:
Если в первом профиле на очередном месте стоит 1, значит во втором обязательно должен стоять 0, так как мы не сможем замостить эту клетку никакой фигуркой.
Если в первом профиле на очередном месте стоит 0, то есть два варианта — или во втором 0 или 1.
Если 0, это значит, что мы обязаны положить вертикальную доминошку, а значит следующую клетку можно рассматривать как 1. Если 1, то мы ставим вертикальную доминошку и переходим к следующей клетке.
Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):
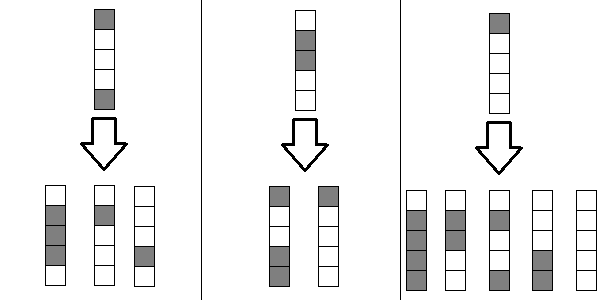
После этого сохранить всё в массив can[mask][next_mask] — 1, если можно перейти, 0 — если нельзя.
1) Состояние динамики: dp[pos][mask] — количество полных замощений первых pos - 1 столбцов с профилем mask.
2) Начальное состояние: dp[0][0] = 1 — левая граница поля — прямая стенка.
3) Формула пересчёта:
dp[pos][mask] += dp[pos - 1][next_mask] * can[mask][next_mask]
4) Порядок обхода — в порядке увеличения pos.
5) Ответ лежит в dp[pos][0].
Полученная асимптотика — 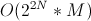 .
.
Динамика по изломанному профилю
Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:
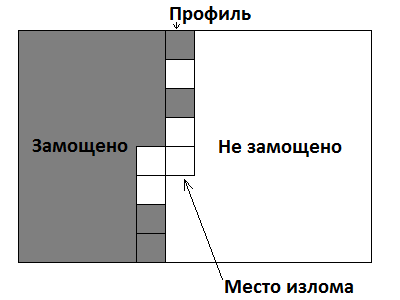
Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с 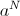 до
до 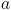 . Асимптотика улучшилась с
. Асимптотика улучшилась с 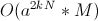 до
до 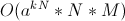 .
.
Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):
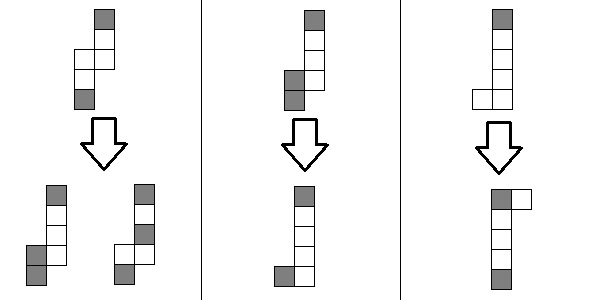
Восстановление ответа
Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.
В каждой задаче свой способ восстановления ответа, но самые распространенные:
- Рядом со значением состояния динамики хранить полный ответ на подзадачу. Если ответ — это что-то большое, то может понадобиться чересчур много памяти, поэтому если можно воспользоваться другим методом, обычно так и делают.
- Восстанавливать ответ, зная предка(ов) данного состояния. Зачастую можно восстановить ответ, зная только как он был получен. В той самой «Запаковке строки» можно для восстановления ответа хранить только вид последнего действия и то, из каких состояний оно было получено.
- Есть способ, вообще не использующий дополнительную память — после пересчёта динамики пойти с конца по лучшему пути и по дороге составлять ответ.
Небольшие оптимизации
Память
Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.
Время
Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в алгоритме Дейкстры [9] можно воспользоваться очередью с приоритетами [10] для изменения асимптотического времени.
Замена состояния
В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.
Пример №9: Разложение числа
Требуется найти количество разложений числа N на различные слагаемые. Например, если N = 7, то таких разложений 5:
- 7
- 3 + 4
- 2 + 5
- 1 + 7
- 1 + 2 + 4
Решение №1:
1) Состояние динамики: dp[n][k] — количество разложений числа n на числа, меньшие или равные k. Параметр k нужен, чтобы брать всегда только большие числа, чем уже имеющиеся.
2) Начальные значения: dp[1][1] = 1, dp[1][i] = 0.
3) Формула пересчёта:
for last_summand in range(1, k + 1):
dp[n][k] += dp[n - last_summand][last_summand]
4) Порядок: прямой, в порядке увеличения n.
5) Ответ — сумма dp[N][1..N].
Состояний: 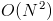 , переходов:
, переходов: 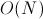 . Асимптотика:
. Асимптотика: 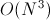 .
.
Решение №2:
1) Поменяем состояние. Теперь dp[n][k] — это количество разложений числа n на k различных чисел. Казалось бы незачем, но сейчас будет понятно.
2) Начальные значения: dp[1][1] = 1, dp[1][i] = 0.
3) Формула пересчёта:
dp[n][k] = dp[n - k][k] + dp[n - k - 1][k + 1]
Теперь надо пояснить, что значит эта формула. Все состояния можно получить (причём единственным способом) делая поочерёдно два действия:
- Все уже имеющиеся числа увеличить на
1. - Все уже имеющиеся числа увеличить на
1. Добавить число1в разложение.
Чтобы понять, почему это так нужно посмотреть на таблицы Юнга [11]:
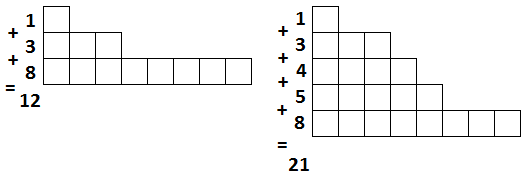
Строки здесь обозначают слагаемые.
Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.
4) Порядок пересчёта: прямой, в порядке увеличения n.
Невооруженным взглядом кажется, что у этого решения асимптотика 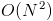 , ведь есть два измерения в состоянии и
, ведь есть два измерения в состоянии и 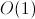 переходов. Но это не так, ведь второй параметр —
переходов. Но это не так, ведь второй параметр — k ограничен сверху не числом N, а формулой 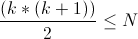 (сумма чисел от
(сумма чисел от 1 до k меньше или равна разлагаемого числа). Из этой формулы видно, что количество состояний 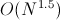 .
.
5) Ответ — это сумма dp[N][1..k_max].
Асимптотика: 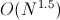 .
.
Заключение
Основным источником была голова, а туда информация попала с лекций в Летней Компьютерной Школе [12] (для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (darnley [13]).
Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.
Автор: Frommi
Источник [14]
Сайт-источник PVSM.RU: https://www.pvsm.ru
Путь до страницы источника: https://www.pvsm.ru/algoritmy/42365
Ссылки в тексте:
[1] мемоизированная: http://ru.wikipedia.org/wiki/Мемоизация
[2] поиска в глубину: http://ru.wikipedia.org/wiki/Поиск_в_глубину
[3] числа Фибоначчи: http://ru.wikipedia.org/wiki/Числа_Фибоначчи
[4] вики: http://ru.wikipedia.org/wiki/Умножение_матриц
[5] метод быстрого возведения в степень: http://en.wikipedia.org/wiki/Exponentiation_by_squaring
[6] Развернутое условие: http://acm.timus.ru/problem.aspx?space=1&num=1238
[7] Дубы: http://habrahabr.ru/post/112386
[8] гамильтонов цикл: http://ru.wikipedia.org/wiki/Гамильтонов_цикл
[9] алгоритме Дейкстры: http://ru.wikipedia.org/wiki/Алгоритм_Дейкстры
[10] очередью с приоритетами: http://ru.wikipedia.org/wiki/Очередь_с_приоритетом_(программирование)
[11] таблицы Юнга: http://en.wikipedia.org/wiki/Young_tableau#Diagrams
[12] Летней Компьютерной Школе: http://lksh.ru/
[13] darnley: http://habrahabr.ru/users/darnley/
[14] Источник: http://habrahabr.ru/post/191498/
Нажмите здесь для печати.