Заметки Датасатаниста: что делать, если перед вами оказалась NP-полная задача

Наверное, каждый сталкивался с тем, что приходилось столкнуться с какой-то сложной задачей, решение к которой не удавалось подобрать не то что сразу — а даже после долгих упорных часов работы или дней. Об одном из классов таких задач — NP-полных, мы сегодня и поговорим.

А вообще реально ли встретить такие задачи в обычной жизни? На самом деле, они возникают в огромном ряде случаев: комбинаторика, графы и сети, выполнение логических формул, работа с картами, оптимальные загрузки, отображения, задачи дискретной оптимизации, нахождение самых длинных последовательностей, поиск равных сумм и многие задачи на множества! И это далеко не полный список.

Под катом неформальный гайд — как понять, что перед вам может быть NP задача и что делать, если это именно она и оказалась. Сегодня мы атакуем этот вопрос с практической стороны.

Убедиться, что перед вам действительно она

Как понять, что перед вами оказалась NP-полная задача? Во-первых, самая простая эвристика на обнаружение — поиск по уже известным NP-полным задачам с целью определить что-то похожее, таких списков немало — например ^[1].

Второе, рассмотреть следующие свойства задач:

• Нужно выбрать решение, в котором n элементов из пространства exp(n)
• Если у вас уже есть решение длины n из этого пространства — оно легко (полиномиально) проверяется
• Выбор одного из элементов решения (может) влияет на выбор всех остальных (не обязательно всех).
• В худшем случае варианты всегда можно перебрать, рассмотрев все экспоненциальное пространство простым перебором.
• Параметры n — длина решения или само пространство не имеют фиксированного значения, то есть речь не идет о всегда фиксированной шахматной доске 8 на 8, а об общем виде задачи N-на-N.

Подробнее про свойства NP-полных задач тут ^[2] и тут ^[3].

Пример работы по данному списку

Приведем простой пример на задаче, которую недавно утвердили как NP-полную!

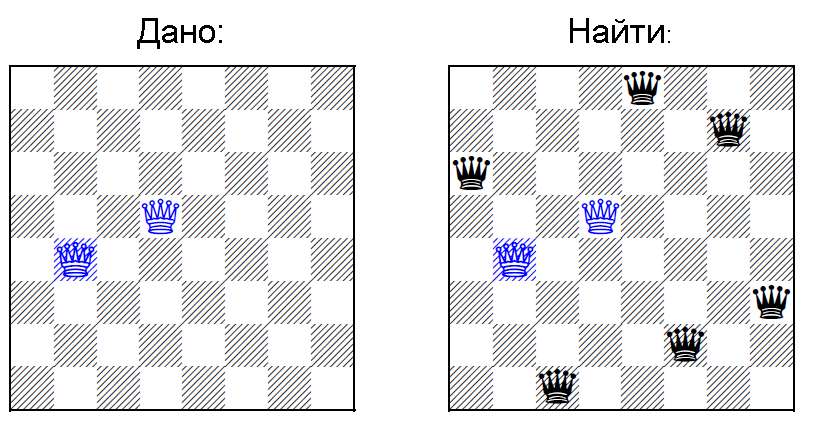
По материалам статьи. ^[4] Нужно расставить N ферзей на доске размера N на N, при условии, что уже K <= N расставлены на доске (картинка из оригинальной научной статьи)

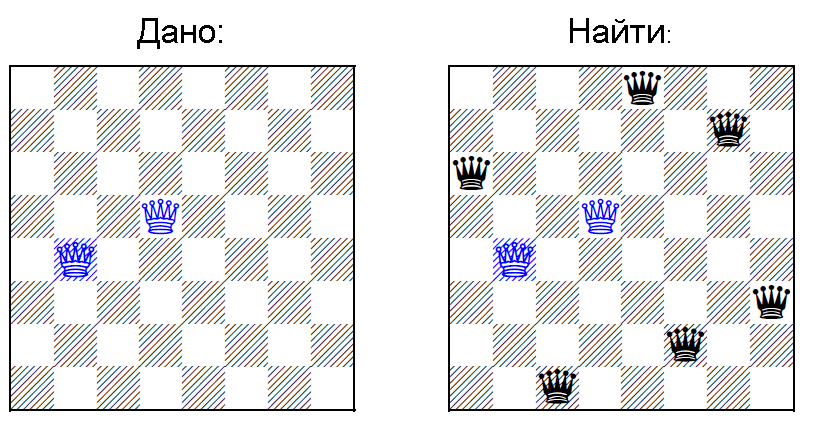
Во-первых, заметим, что очень похожая задача ^[5] с частично заставленным латинским квадратов NP полна.

А далее идем по списку:

• Нужно найти N ферзей на из пространства exp(N) (=N^2 * (N^2-1) *....).
• Решение из N ферзей тривиально проверяется — для каждого ферзя надо проверить диагонали, вертикали и горизонтали.
• Постановка одного делает выбор ряда других невалидным — т.е. есть зависимости между элементами решения (нельзя расставить ферзей независимо).
• Здесь можно решить задачу перебором для произвольно выбранной доски за exp(N) — ставим первого в первого на (i,j) позицию, второго на любую другую незанятую, и тд. Перебор с возвратом гарантированно найдет решение.
• Задача не имеет фиксированных параметров — то есть сформулирована в общем виде и по мере роста N растет и сложность.

Заметьте, что один из пунктов списка не выполняется, если всегда известно, что доска чистая и задача становится тривиальной.

И более того, это условный практический подход — эвристика по обнаружению NP-полных задач (со всеми плюсами и минусами).

Сведение

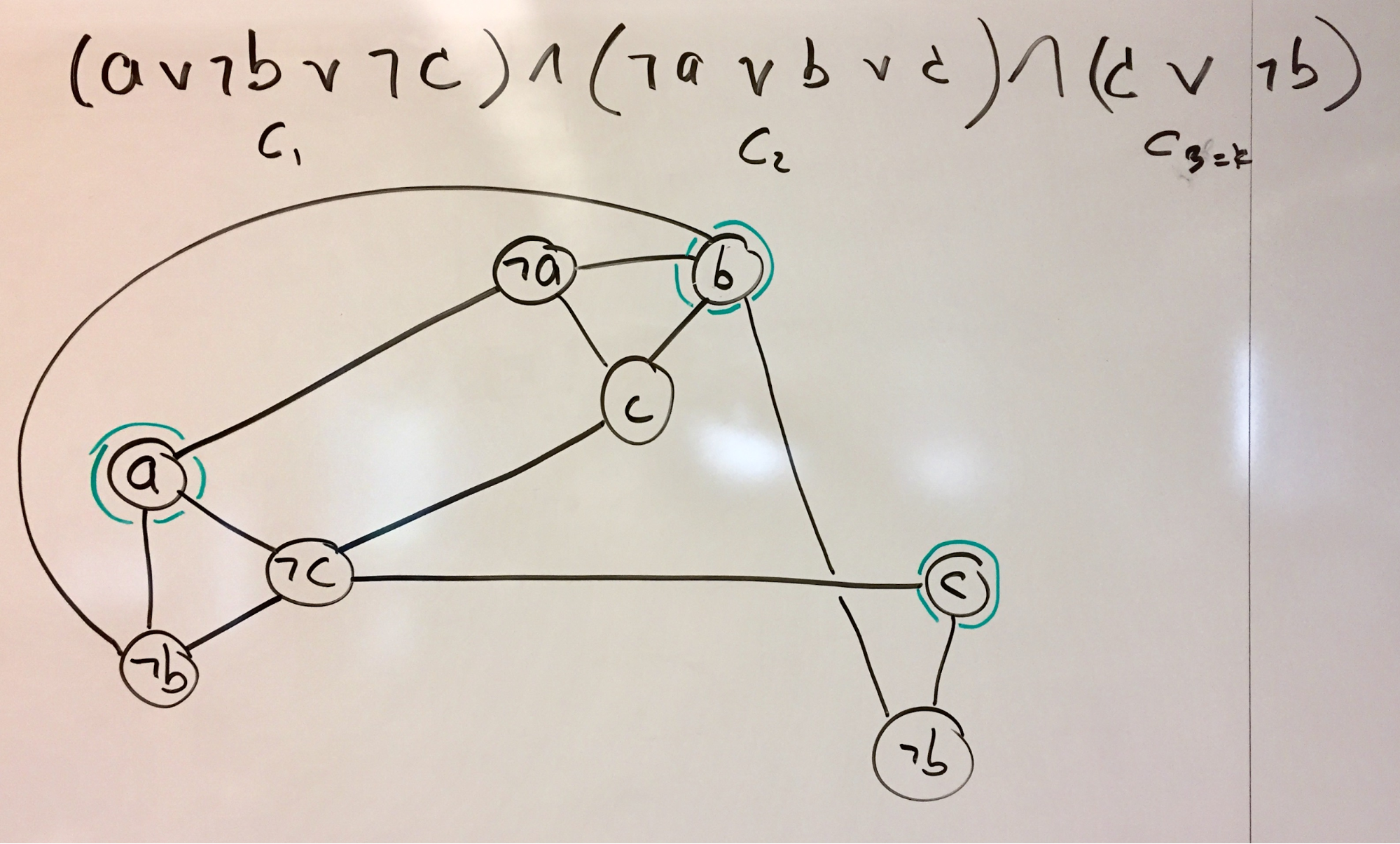
Источник ^[6]

Почему имея на руках аналогичные задачи бывает непросто понять формально, что перед нами NP-задача? По-настоящему мы должны свети NP задачу к нашей, тогда мы точно будет знать, что наша задача NP-трудная! И если мы смогли ее смоделировать, как в списке выше, то она полная — то есть по крайней мере NP и не более чем NP, фактически “самая трудная среди NP задач” (как и остальные NP-полные).

Окей, надо ли оно нам? Не совсем, если вы прям уверены, после всех проверок, что перед вами NP-задача, то вам не нужно ничего доказывать, если вы не пишите научную статью.

А нужно либо (об этом всем мы поговорим ниже):

• смоделировать свою задачу с помощью систем, которые решают такие задачи;
• найти решение, который будет работать достаточно быстро в вашем случае;
• найти приближенное решение, которое удовлетворит нас.

Не опускать руки!

Самое важное — это оценить размеры-параметры и реалистичные сценарии!

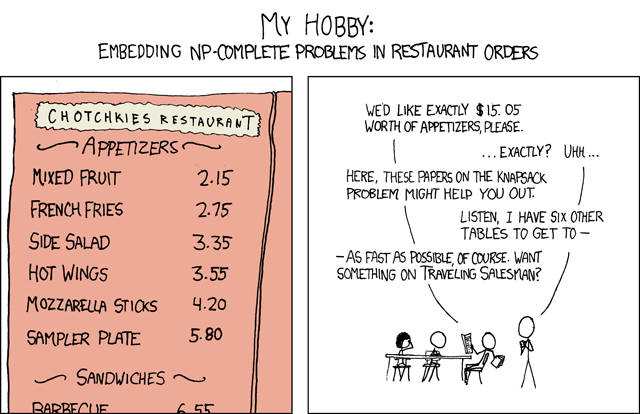
xkcd.com/287 ^[7]

Например, вы знаете, что несмотря на то, что значения параметров не фиксированы, но условный N < 100 на всех практических сценариях не реализуется — значит, что условный перебор может для вас быть реальным решением.

Вам нужно определить для себя: какие у меня реальные значения параметров возможные и реально приходят в систему, какое вообще распределение и особенности данных, что реально, а что нет? А нужно ли нам самое оптимальное решение? Пройдемся по этим пунктам.

Распределение входных данных

Или несмотря на то, что в общем случае входные данные могут быть любыми, но опять же на примере ферзей — обычно фиксирован один ферзь или даже ни одного. Значит, что в 90% случаев вы можете использовать очень простое решение и вызывать сложное только в крайних случаях.

Пример, когда в среднем все обычные комбинации простые: задача о дополнении ферзей — мы знаем, что условный DFS + эвристики могут в большинстве случаев находить решения очень быстро, и только в очень нестандартных ситуациях быть крайней сложными.

Вот пример, того как оценивалось решение для очень специализированной задачи NP-полной tiling против общего метода моделирования целого класса таких задач с помощью методов логического программирования:

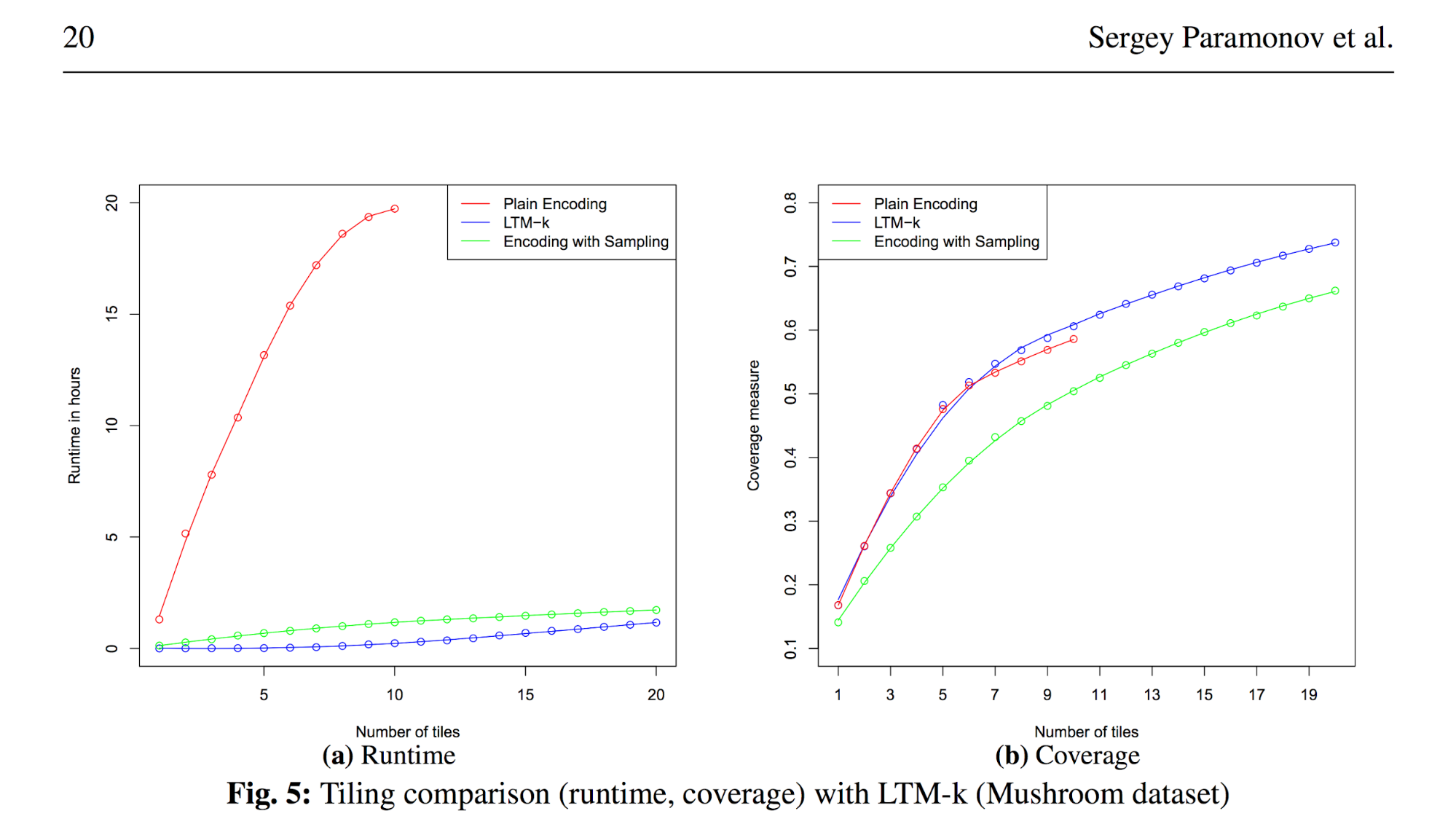
(из статьи Relational Data Factorization ^[8] (Paramonov, Sergey; van Leeuwen, Matthijs; De Raedt, Luc: Relational data factorization, Machine Learning, volume 106))

Во-первых, скорость у спец решения LTM-k и общего метода существенно отличаются. Таким образом решение для именно такого типа задач на эвристиках может полностью решать эту проблему.

Во-вторых, пожертвовав качеством решения, общий приближенный метод давал очень похожую скорость.

Эвристики и аппроксимация

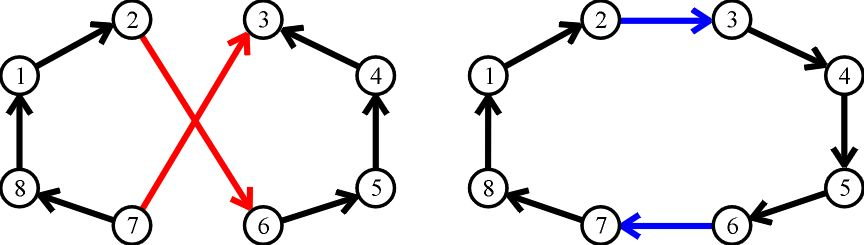
Последний и самый мощный инструмент — это использовать системы моделирования NP-полных задач, такие как например Answer Set Programming ^[9].

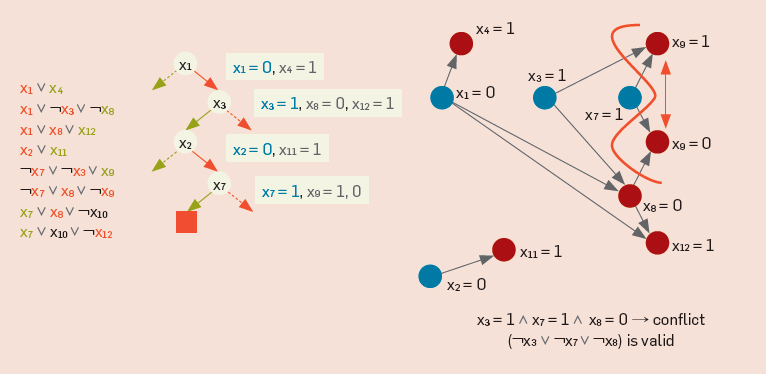
Подробнее про языки логического программирования. ^[10]
Например решение задачи о расстановке ферзей будет выглядеть вот так:

% domain
row(1..n).
column(1..n).

% alldifferent: guess a solution
1 { queen(X,Y) : column(Y) } 1 :- row(X).
1 { queen(X,Y) : row(X)    } 1 :- column(Y).

% remove conflicting answers: check this solution
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 - X1 == Y2 - X2.

Проведя простой эксперимент по поиску решений для разного количества ферзей N — мы получим следующее: по оси Х — ферзи, по Y — время в секунда по поиску решения:

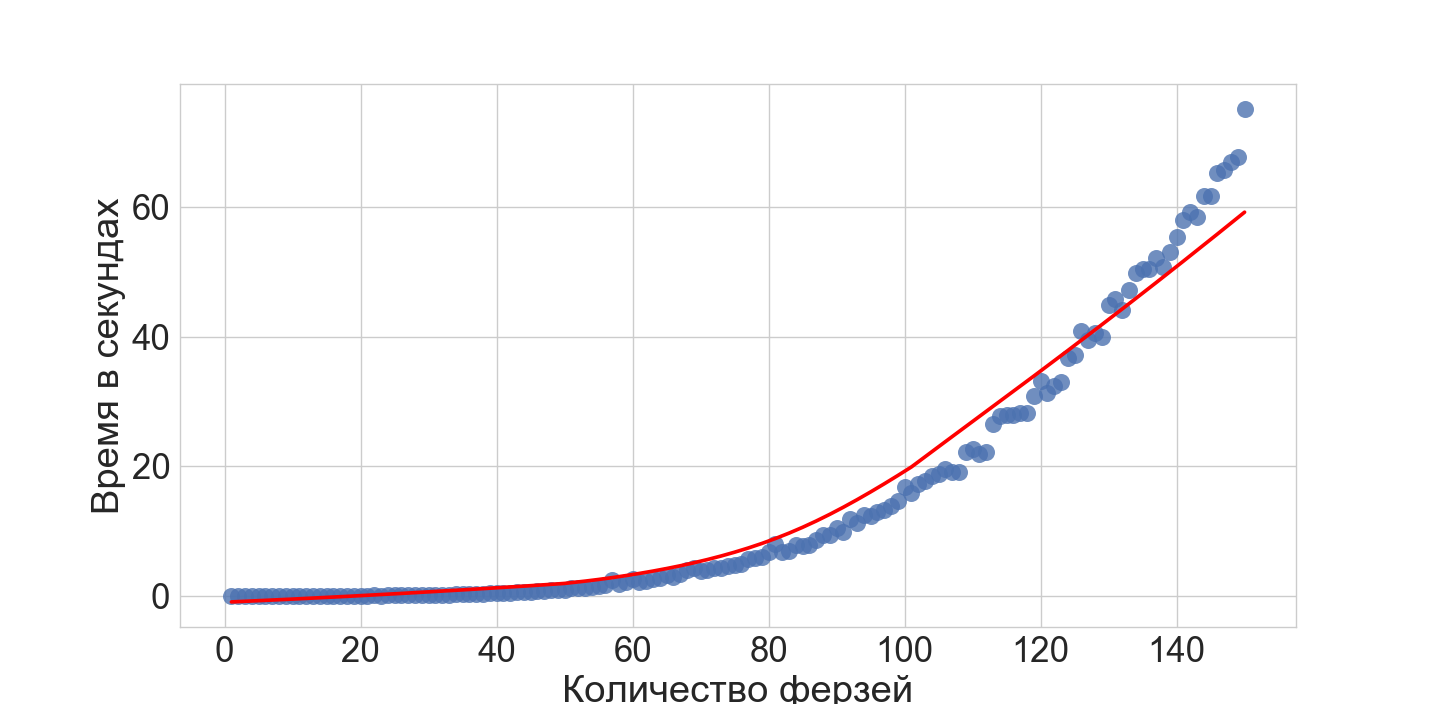
Мы видим, что несмотря на то, что рост времени явно не полиномиальный (что и логично) мы хорошо справляемся с адекватным количеством ферзей и размерами доски.

Тогда, если мы знаем, какие размеры доски являются для нас реальным, мы можем понять насколько это точное решение приемлемо для нас в настоящей системе.

Выводы

Тезисно пройдемся, по идеям из статьи в виде чек листа

• Определить, что перед вами действительно NP задача.
• Понять какие реалистичные значения параметров и распределение данных.
• Попробовать написать (порядок зависит от разработчика и/или задачи):
  • Точное решение на эвристиках (на основе нашего анализа) — будет ли достаточно быстро?
  • Приближенное решение на эвристиках — будет ли достаточно точно?
  • Точное общее решение с помощью систем моделирования NP-задач — будет ли удовлетворять ресурсам системы и задачи? Потребление памяти, CPU и время работы? Часто они очень прожорливы.
• Провести эксперименты и сравнить решения: качество, время и корректность найденных решений.
• Тестирование на реальной системе — эксперименты экспериментами, а как будут вести себя библиотеки и системы разработанные в университетах в боевых условиях — еще та загадка. Надо проверять!

Другие заметки Дата Сатаниста:

^[18]

Автор: paramonov_ruvds

Источник ^[19]