Облачные вычисления / Введение в теорию взаимодействующих последовательных процессов (CSP), часть 2

Продолжаем цикл статей посвящённый алгебре исчисления процессов. Данный текст является переводом и сокращённым пересказом начальных глав книги ^[1] Чарльза Э. Хоара ^[2]. Теория применяется для формального описания работы параллельных систем. Примерам её практических применений являются такие языки программирования как Erlang, Go и Limbo.

• Часть 1 ^[3]
• Часть 2

Выбор

С помощью рекурсии и префиксов мы можем описать объект с единственно возможным линейным поведением. Однако, многие объекты находятся под влиянием внешних условий, а значит могут реагировать действовать тем или иным образом в зависимости от ситуации. Например, торговый автомат может иметь отверстия для однорублёвых и двухрублёвых монет и уже от покупателя будет зависеть какая монета будет вставлена в автомат. Таким образом, если x и y различные события, то запись:

(x → P | y → Q)

описывает объект, который изначально участвует в событии либо x, либо y. Если произошло событие x, то объект ведёт себя далее как P, если же произошло y, то он будет вести себя как Q. Т.к. x и y есть различные события, то выбор между P и Q является предопределённым тем какое событие произойдёт первое x или y. Как и ранее мы утверждаем постоянство алфавитов, т.е.:

α(x → P | y → Q) = αP = αQ, подразумевая что {x, y} ⊆ αP

Палка "|" произносится как «выбор»: «x затем P выбор y затем Q».

Примеры

1. Возможные движения указателя по доске:
   
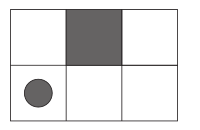
   описываются как:
   
   

   (up → STOP | right → right → up → STOP)
2. разменная машина, которая позволяет пользователю выбрать каким образом произвести размен (сравните с разменными машинами описанными ранее):
   
   

   CH5C = in5p → (out1p → out1p → out1p → out2p → CH5C          | out2p → out1p → out2p → CH5C)
3. Торговый автомат продающий либо шоколадку, либо карамельку:
   
   

   VMCT = μX • coin → (choc → X | toffee → X)
4. Более сложная торговая машина дающая покупателю выбор какие монеты использовать и какого размера шоколадку получать:
   
   

   VMC = (in2p → (large → VMC                 | small → out1p → VMC)         | in1p → (small → VMC                   | in1p → (large → VMC                             | in1p → STOP )))

   Как и многие сложные машины она имеет конструктивный изъян. Зачастую легче изменить пользовательские инструкции, нежели чем исправлять саму машину, так что давайте напишем на машине:
   «ВНИМАНИЕ: не вставляйте три однорублёвых монеты подряд.» (хотя кого мы обманываем, в наших условиях этим мы только приблизим заклинивание машины)

5. Автомат который доверяет пользователю и позволяет попробовать шоколадку и уже потом заплатить:
   
   

   VMCRED = μX • (coin → choc → X                 | choc → coin → X)
6. Для предотвращения убытков воспользуемся начальным платежом для получения привилегии использовать VMCRED:
   
   

   VMS2 = (coin → VMCRED)

   Данный автомат позволяет вставить две монетки подряд и получить две шоколадки подряд, но никогда не отдаст шоколадок больше чем было оплачено монет.

7. Копирующий процесс участвует в следующих событиях:
   
   • in.0 — подача нуля на вход
   • in.1 — подача единицы на вход
   • out.0 — подача нуля на выход
   • out.1 — подача удиницы на выход

   Поведение процесса требует повторения пар вход-выход, таким образом мы можем описать его как:

   COPYBIT = μX • (in.0 → out.0 → X                  | in.1 → out.1 → X )

   Заметьте, процесс позволяет выбирать что подать на вход, в то время как для выхода никакого выбора нет. Именно эта особенность будет главной разницей между входом и выходом процесса при обсуждении в дальнейшем передачи сообщений между процессами.

Определение выбора может быть естественно расширено на большее количество событий, т.е.:

(x → P | y → Q |... | z → R)

Обратите внимание, что символ "|" не является оператором над процессом, будет синтаксически неверно писать P | Q, для процессов P и Q. Причина данного правила в том, что мы не хотим избежать определять значение следующей записи:

(x → P | x → Q )

Которое вроде бы даёт выбор, но на самом деле не делает этого. Данная проблема в будущем решается с помощью введения неопределённости поведения.

Таким образом, если x, y, z различные события, то:

(x → P | y → Q | z → R)

должно восприниматься как один оператор с тремя аргументами P, Q, R. Данный оператор не является равным записи:

(x → P | (y → Q | z → R))

которая является синтаксически некорректной.

Обобщая, если B есть множество событий и P(x) есть выражение определяющее процесс для каждого x из B, тогда выражение:

(x: B → P(x))

определяет процесс который в начале предлагает выбрать любое событие y из B, после чего ведёт себя как P(y). Данное выражение должно произноситься как "x из B затем P от y". В данной конструкции x является локальной переменной, таким образом:

(x: B → P(x)) = (y: B → P(y))

Множество B определяет образно говоря меню процесса, т.е. те действия на которые процесс способен ответить.

Пример

1. Процесс который всегда может участвовать во всех событих из своего алфавита:
   
   

   αRUN_A = A
   RUN_A = (x: A → RUN_A)

В особом случае, когда меню содержит всего одно событие e:

(x: {e} → P(x)) = (e → P(e))

В ещё более особом случае, когда меню пусто, следовательно ничего не может произойти:

(x: {} → P(x)) = (y: {} → P(y)) = STOP

Таким образом остановка, префикс и бинарный выбор являются особыми случаями общей записи, что будет достаточно удобно при формулировке далее общих законов касающихся процессов и описания их реализации.

Косвенная рекурсия

Обычная рекурсия позволяет определить процесс как решение одного уравнения. Данная методика легко расширяема на систему уравнений с более чем одним неизвестным. Для того что бы данная система была корректна необходимо что бы правые части были защищены и что бы каждый неизвестный процесс появлялся хотя бы единожды в правой части какого-либо уравнения системы.

Примеры

1. Автомат по продаже напитков имеет две кнопки «апельсин» и «лимон», нажатие на которые активирует события setorange и setlemon соответственно. Выбор напитка, который будет налит, производится нажатием соответствующей кнопки. По нажатию кнопки dispense будет разлит тот или иной напиток. До того как режим не был выбран напиток разливаться не будет, запишем это изначальное состояние как DD. Используя два вспомогательных процесса O и L опишем алфавит и поведение DD:
   
   

   αDD = αO = αL = {setorange, setlemon, dispense}
   DD = (setorange → O | setlemon → L)
   O = (dispense → O | setlemon → L | setorange → O)
   L = (dispense → L | setorange → O | setlemon → L)

   Видно что после выбора режима в самом начале (назовём это начальной настройкой автомата) машина пребывает в одном из двух состояний, в каждом из которых она разливает определённый напиток и из которых она может переходит во второе состояние. Можно находясь в «апельсиновом» режиме нажать кнопку «апельсин», но никакого эффекта это не принесёт.

2. Используя пронумерованные переменные мы можем задать бесконечное множество уравнений. Пусть объект стартует на земле и может двигаться по земле (назовём это действие around) и может подниматься вверх (назовём это действие up). Находясь в воздухе объект может либо подняться выше (up), либо опуститься вниз (down), но будучи на земле он не может опуститься ещё ниже. Таким образом взяв множество n натуральных чисел (0, 1, 2, ...) мы можем записать поведение этого объекта как:
   
   

   CT₀ = (up → CT₁ | around → CT₀)
   CT_n+1 = (up → CT_n+2 | down → CT_n)

   Первое уравнение описывает поведение объекта на земле, а все остальные в воздухе.

   Таким образом через косвенную рекурсию мы определили бесконечное множество правил описывающих работу нашего процесса.

Заключение

Для удобства чтения и написания размер статей несколько сокращён, надеюсь за счёт этого у меня получится писать их почаще.

В следующей части будет показано графическое представление процессов, вывод базовых законов и реализация модели процессов. Последнее в книге осуществлено с помощью лиспа, я же попытаюсь переписать примеры на питоне, как более знакомом и понятном для многих, за что будет заплачено потерей некоторой нативности переноса.

Автор: newpavlov