Анализ комбинации жадного алгоритма поиска клики с частичным перебором вершин графа

Доброго времени суток.

В свободное время провёл небольшое исследование.

В теории графов известен жадный алгоритм поиска кликового числа. Далеко не всегда он даёт верный результат. Под катом проводится анализ результатов работы жадного алгоритма при его комбинации с частичным перебором множеств вершин на графах из «DIMACS benchmark set».

В столбце «Best known» таблицы 1 приведены размеры известных на данный момент максимальных клин указанных графов. В столбце «Greedy» указаны значения размеров максимальных клик, найденных жадным алгоритмом. Жадный алгоритм выдаёт верный ответ лишь в 3 случаях из 35.

Примечание – в реализованном программном коде жадный алгоритм выбирает вершину с наибольшим значением смежности. Если найдено несколько подобных вершин, выбирается первая найденная. Назовём процедуру жадного алгоритма Greedy(A), где А – номер массива (матрицы смежности), к которому применяется алгоритм. Изначальный массив проиндексируем как А0.

Таблица 1 – Результаты работы алгоритма, реализованного на языке Pascal.

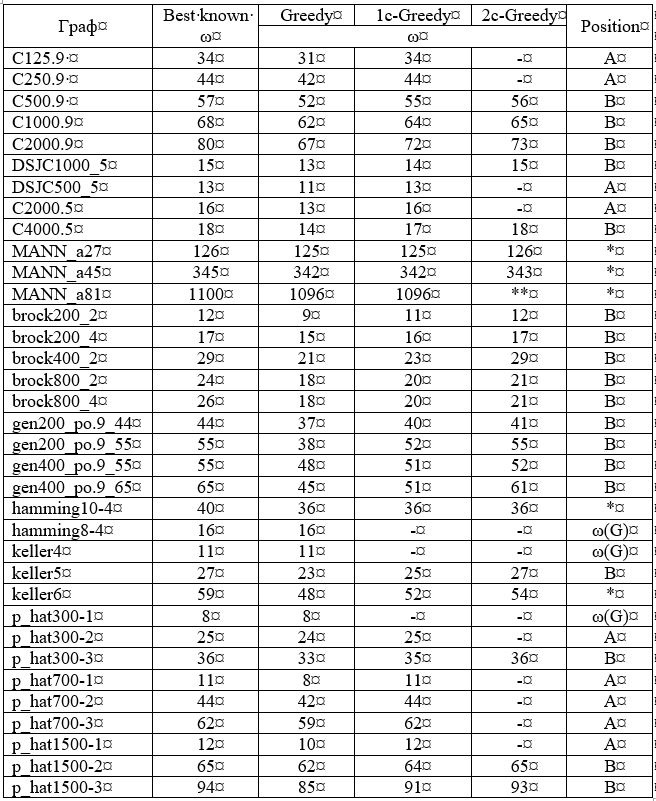
** — не анализировалось ввиду большого размера графа.

Сделаем следующий шаг, а именно: будем поочерёдно брать все N вершин графа, отсекая при этом не смежные. Обозначим полученные массивы как Аm, где m – номер выбранной вершины. Такую процедуру в алгоритме обозначим как DelNotAdj(m).

К получаемым подграфам снова применим процедуру Greedy(Аm). Результаты (максимальный размер найденных клик) приведены в столбце «1c-Greedy». Можно заметить, что найденных верных результатов стало больше, а именно 8 из 35.

Теперь рассмотрим парные комбинации смежных вершин. Алгоритмически это будет означать, что мы дважды применим процедуру DelNotAdj(m). Сначала для изначального графа А0, затем для каждой из вершин получаемых Аm. Обозначим получаемые подграфы как Аmx. И вновь воспользуемся Greedy(Аmx). Результаты (максимальный размер найденных клик) приведены в столбце «2-Greedy».

Были также проанализированы комбинации из 3-х вершин (3c-Greedy) для графов C500.9 и C1000.9 с соответствующими результатами ω(C500.9)=57, ω(C1000.9)=66.

На некоторое время отложим анализ результатов работы алгоритмов и рассмотрим их теоретическую временную сложность.

В реализации на языке Pascal процедура жадного алгоритма Greedy(A) имеет временную сложность порядка O(n²), где n – количество вершин в исходном графе. Перебор всех вершин графа усложняет алгоритм в n раз, перебор комбинаций из 2-х – в раз и т.д. вплоть до полного перебора , где ω(G) – размер максимальной (искомой) клики. В последнем случае применение жадного алгоритма лишено смысла.

Возникает вопрос, как определить, каким перебором можно ограничиться? Из таблицы 1 невозможно выявить четкую закономерность, однако попытаемся осуществить условную классификацию.

Построим графики некоторых найденных значений (рисунок 1). По оси абсцисс отложим значения порядка временной сложности O(n), по оси ординат – возможные значения найденных размеров клик ω от 1 до ω(G) – максимального значения, ω_GR – размер клики, найденной жадным алгоритмом в исходном графе.

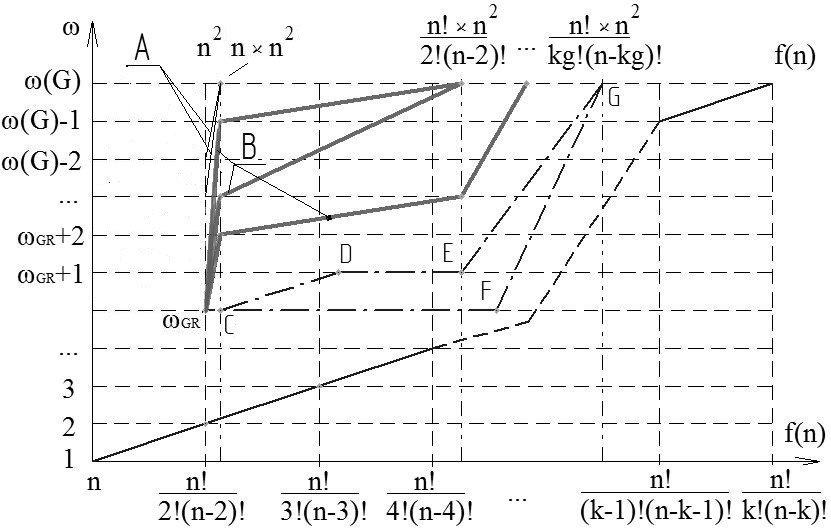
Рисунок 1

Позиционные обозначения групп построенных графиков приведены в столбце «Position» таблицы 1 для соответствующих графов. ꞷ(G) обозначены графы, для которых жадный алгоритм выдаёт верный результат без перебора. В группу «А» попали графы, для которых уже однократный перебор вершин приводит к нахождению клики заданного размера.

В группу «B» вошли графы, требующие для нахождения верного ответа 2-х и более кратный перебор.

В группу «*» вошли графы, имеющие «полку», т.е. найденные значения размеров клик начиная с просто жадного алгоритма и до перебора 2, 3 и более комбинаций вершин не изменяются. Затем следует увеличение значения ω. Такое поведение обозначено на рисунке отрезками ω_GRCFG.

Можно утверждать, что для конкретной вершины и, следовательно, для всего графа в целом, график зависимости размера найденной максимальной клики от количества переборов не будет убывать. Т.е. перебрав все комбинации из вершин, смежных выбранной, мы получим результат не хуже, чем при переборе комбинаций из 2-х вершин.

Обозначим «алгоритмом» последовательность действий по нахождению клики заданного размера, такую что:

1. На первом шаге к исходному графу А0 применяется «жадный» алгоритм. Полученное значение размера клики обозначим как ω_GR.
2. На втором шаге применим последовательно «жадный» алгоритм к подграфам Аm, образованным каждой m вершиной исходного. При этом подграф Аm не должен содержать вершин, не смежных выбранной. Максимальное найденное значение размера клики обозначим как ωGR+1.
3. На третьем шаге применим последовательно «жадный» алгоритм к подграфам Аmn, образованным комбинациями смежных m-й и n-й вершин исходного графа А0. При этом подграф Аmn не должен содержать вершин, не смежных n-й и m-й вершинам. Максимальное найденное значение размера клики обозначим как ω_GR+2.
4. Максимальные найденные значения размеров клик для комбинаций 3-х, 4-х,…, y-вершин обозначим как ω_GR+3, ω_GR+4,…, ω_GR+y соответственно.
5. Кликовое число для графа А0 — ω(G).

Предлагается две гипотезы. Первая относится к графам группы «А» и «B» может быть сформулирована следующим образом:

Предположим, что значение размера клики, найденной жадным алгоритмом в исходном графе равно ω_GR. Если при однократном переборе вершин с последующим приложением к образованным ими подграфам жадного алгоритма найдено хотя бы одно значение ω_GR+1 большее ω_GR, то клика искомого размера может быть найдена с временной сложностью порядка 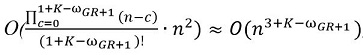, где K – искомое значение размера клики.

Для группы под «*» гипотеза выглядит так:

В общем случае последовательность значений размеров найденных «алгоритмом» клик ω_GR, ω_GR+1, ω_GR+2,…, ω(G) неубывающая. При этом данная последовательность может иметь не более одного промежутка, такого, что каждый последующий элемент равен предыдущему. Если такой промежуток существует, то его нижняя граница равна ω_GR.

Проиллюстрировать данную гипотезу можно следующим образом: не существует последовательности значений ω_GR, ω_GR+1, ω_GR+2,… такой, что она образует «промежуточную полку» (отрезки ω_GRCDE рисунка 1).

В случае корректности второй гипотезы из неё могут существовать два следствия:

Следствие 1. Если при работе «алгоритма» найдено значение ω_GR+y, большее
ω_GR+y-1, то клика искомого размера может быть найдена с временной сложностью порядка 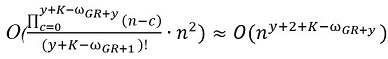, где K – искомое значение размера клики.

Данное свойство является обобщением первой гипотезы.

Свойство 2. Если на y-м шаге найдено такое же значение ω_GR+y, что и на предыдущем шаге, т.е. ω_GR+y=ω_GR+y-1, следовательно, найденное значение ω_GR+y является кликовым числом ω(G) для исходного графа.

Если изложенное повторяет чью-то работу, я не со зла, буду рад ссылке для ознакомления. Еще больше буду рад, если кто-то теоретически сможет доказать или опровергнуть предложенные гипотезы.

Автор: Inzer

Источник ^[1]