Методы экспертных оценок

Зачастую необходимо выбрать среди множества альтернатив, при этом каждая обладает различными преимуществами. И как же выбрать лучшую, имея мнение десятков, а то и сотен экспертов?


Как вычисление рейтинга компьютерной игры, основанного на оценках критиками графики, геймплея и сюжета, так и коллективный выбор приоритетной задачи перед появлением заказчика, относится к методам экспертных оценок ^[1].

Краткий ликбез

Методы экспертных оценок являются частью обширной области теории принятия решений ^[2], а само экспертное оценивание — процедура получения оценки проблемы на основе мнения специалистов (экспертов) с целью последующего принятия решения (выбора).

В случаях чрезвычайной сложности проблемы, ее новизны, недостаточности имеющейся информации, невозможности математической формализации процесса решения приходится обращаться к рекомендациям компетентных специалистов, прекрасно знающих проблему, — к экспертам. Их решение задачи, аргументация, формирование количественных оценок, обработка последних формальными методами получили название метода экспертных оценок.

Существует две группы экспертных оценок:

1. Индивидуальные оценки основаны на использовании мнения отдельных экспертов, независимых друг от друга.
2. Коллективные оценки основаны на использовании коллективного мнения экспертов.

Грубо говоря, к первой группе относится оценка статей на хабре, голосование в опросах и т.д., когда каждый эксперт принимает решение самостоятельно. Подбор (отсев) экспертов осуществляется посредством кармы. Именно первая группа превалирует в интернете 2 за счет возможности охвата большего числа экспертов.

Способы измерения объектов

1. Ранжирование – это расположение объектов в порядке возрастания или убывания какого-либо присущего им свойства. Ранжирование позволяет выбрать из исследуемой совокупности факторов наиболее существенный.
2. Парное сравнение — это установление предпочтения объектов при сравнении всех возможных пар. Здесь не нужно, как при ранжировании, упорядочивать все объекты, необходимо в каждой из пар выявить более значимый объект или установить их равенство.
3. Непосредственная оценка. Часто бывает желательным не только упорядочить (ранжировать объекты анализа), но и определить, на сколько один фактор более значим, чем другие. В этом случае диапазон изменения характеристик объекта разбивается на отдельные интервалы, каждому из которых приписывается определенная оценка (балл), например, от 0 до 10. Именно поэтому метод непосредственной оценки иногда именуют также балльным методом.

Метод простой ранжировки заключается в том, что каждого эксперта просят расположить признаки в порядке предпочтения.

a_ij — оценка признака экспертом. n — количество признаков, m — количество экспертов.
Затем, подсчитывается S_i — среднее значение ^[3] важности признака.

Метод задания весовых коэффициентов (a_ij)

1. всем признакам назначают весовые коэффициенты так, чтобы суммы коэффициентов была равна какому-то фиксированному числу (например, единице, десяти или ста);
2. наиболее важному из всех признаков придают весовой коэффициент, равный какому-то фиксированному числу, а всем остальным – коэффициенты, равные долям этого числа.

Метод последовательных сравнений заключается в следующем:

1. эксперт упорядочивает все признаки в порядке уменьшения их значимости: А1>A2>…>An;
2. присваивает первому признаку значение, равное единице: A1=1, остальным же признакам назначает весовые коэффициенты в долях единицы;
3. сравнивает значение первого признака с суммой всех последующих.

В парном сравнении не нужно, как при ранжировании, упорядочивать все объекты, необходимо в каждой из пар выявить более значимый объект или установить их равенство. Парное сравнение можно проводить при большом числе объектов, а также в тех случаях, когда различие между объектами столь незначительно, что практически невыполнимо их ранжирование.
При использовании метода чаще всего составляется матрица размером n_xn, где n – количество сравниваемых объектов.

При сравнении объектов матрица заполняется элементами a_ij следующим образом (может быть предложена и иная схема заполнения):

• 2, если объект i предпочтительнее объекта j (i > j),
• 1, если установлено равенство объектов (i = j),
• 0, если объект j предпочтительнее объекта i (i < j).

Непосредственная оценка. Часто бывает желательным не только упорядочить (ранжировать объекты анализа), но и определить, на сколько один фактор более значим, чем другие. В этом случае диапазон изменения характеристик объекта разбивается на отдельные интервалы, каждому из которых приписывается определенная оценка (балл), например, от 0 до 10. Именно поэтому метод непосредственной оценки иногда именуют также балльным методом.

А теперь, самое вкусное...

Анализ результатов экспертных оценок

Для анализа результатов применяются различные методы математической статистики ^[4]. Причем, они могут комбинироваться и варьироваться в зависимости от типа задачи и необходимого результата.

Формирование обобщенной оценки

Итак, пусть группа экспертов оценила какой-либо объект, тогда x_j – оценка j-го эксперта, где m – число экспертов.
Для формирования обобщенной оценки группы экспертов чаще всего используются средние величины ^[3]. Например, медиана ^[5], за которую принимается такая оценка, по отношению к которой число больших оценок равняется числу меньших.
Определение относительных весов объектов
Иногда требуется определить, насколько тот или иной фактор (объект) важен (существенен) с точки зрения какого-либо критерия. В этом случае говорят, что нужно определить вес каждого фактора. Отличается от формирования обобщенной оценки тем, что определяется не общая оценка объекта, а оценка для каждого его признака.
А так же
Существует огромное множество возможных методов обработки оценок.
Как вариант, использовать систему рейтинга Эло ^[6] для метода парных сравений.
Причем, результат может состоять из нескольких алгоритмов, переплетаясь с другими. Например, алгоритм расчета коэффициента компетентности эксперта ^[7] может влиять на среднестатистическую оценку этого эксперта и т.д.

Установление степени согласованности мнений экспертов

В случае участия в опросе нескольких экспертов расхождения в их оценках неизбежны, однако величина этого расхождения имеет важное значение. Групповая оценка может считаться достаточно надежной только при условии хорошей согласованности ответов отдельных специалистов.
Для анализа разброса и согласованности оценок применяются статистические характеристики – меры разброса или статистическая вариация ^[8].
Итак, способы вычисления меры разбрса:
_{В недоступных картинках — формулы. Насколько я понял, на данный момент они кешурются в habrastorage ^[9]}
Вариационный размах ^[10]

Среднее линейное отклонение ^[11]

Среднеквадратическое отклонение ^[12]

Дисперсия ^[13]

Коэффициента ранговой корреляции Спирмэна ^[14]

Коэффициент (величина ) может изменяться в диапазоне от –1 до +1. При полном совпадении оценок коэффициент равен единице. Равенство коэффициента минус единице наблюдается при наибольшем расхождении в мнениях экспертов.
x_ij – ранг (важность), присвоенный i-му объекту j-ым экспертом, x_ik – ранг, присвоенный i-му объекту k-ым экспертом, d_i – разница между рангами, присвоенными i-му объекту.

Коэффициент конкордации Кенделла ^[15]
Коэффициент может принимать значения в пределах от 0 до 1. При полной согласованности мнений экспертов коэффициент конкордации равен единице при полном разногласии – нулю. Наиболее реальным является случай частичной согласованности мнений экспертов.

Вычисление

Определяется средний ранг совокупности признаков:

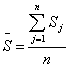
Вчисляется отклонение d_j среднего ранга j-го признака от среднего ранга совокупности:

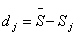
Определяется число одинаковых рангов, назначенных экспертами j-му признаку – t_q.
Определяется количество групп одинаковых рангов – Q. Определяется коэффициент конкордации по формуле:

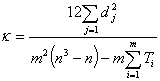
где

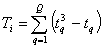
Заключение

Статья и не претендует на полный многоэтапный разбор методов и алгоритмов оценки, лишь поверхностное их описание. Посему, если вы знаете применимые в данном случае (не описанные мной) методы и алгоритмы — с удовольствием добавлю их в статью. Или любую полезную тематическую литературу.

Засим откланиваюсь. Всех с праздником, раминь. А для тех, кто зашел посмотреть на девушек — вот вам

Ссылки:

Википедия — свободная энциклопедия ^[16]
www.rae.ru ^[17]
emm.ostu.ru ^[18]
teorver-online.narod.ru ^[19]
www.habarov.spb.ru ^[20]

Автор: eximap

Источник ^[21]