Изгибаемые многогранники

Посмотрим на многугольник с жесткими сторонами, в вершинах которого помещены шарниры. Если у него более трех вершин, то он может изгибаться — длины сторон далеко не однозначно определяют многоугольник. А что происходит с многогранниками в трехмерном пространстве? Если зафиксировать форму их граней, смогут ли они изгибаться?

Оказывается, что иногда могут, но это очень редкое свойство

Сразу скажем, что под изгибанием понимается непрерывное изгибание, а не просто то, что многогранник не однозначно задается своими гранями. Такой пример придумать довольно легко:

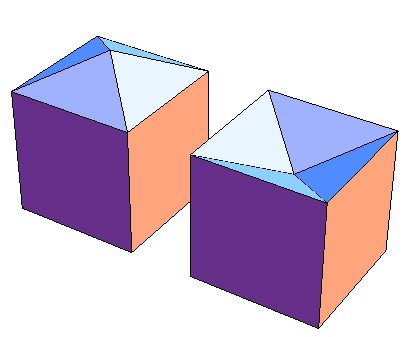
Однако, еще в 1813 году Коши доказал ^[1], что для выпуклого многогранника даже такая ситуация невозможна: выпуклый многогранник однозначно определяется своими гранями.

В 1897 году удалось построить примеры самопересекающихся изгибаемых многогранников(наглядно это можно представить как каркас из проволоки, отсутствие жестких граней не имеет значения, так как все они треугольные и однозначно определяются ребрами) — октаэдры Брикара. Wolfram demonstration ^[2]

Только в 1976 году Конелли предложил конструкцию несамопересекающегося невыпуклого изгибаемого многогранника. Следуя его идеям, Штеффен вскоре построил пример изгибаемого многогранника с 9 вершинами(позже было доказано, что с меньшим количеством вершин это сделать невозможно). Видео с этим многогранником размещено в начале поста, также имеется Wolfram demonstration ^[3].

Оговорим заранее, что рассматриваются многогранники с треугольными гранями. Это не меняет сути дела, так как у любого изгибаемого многгранника можно добавить ребра, разрезав грани на треугольники, от чего его изгибаемость не пропадет. Однако, это упрощает вычисления, так как теперь вся информация о гранях многогранника содержится в комбинаторном строении и длинах ребер.

Попробуем теперь понять, почему оказалось так сложно найти изгибаемые многранники, в то время как для многоугольников это очень типичное свойство. Посмотрим на многугольник с n вершинами. Его форма задается координатами вершин, которых 2n. Эти координаты задают не только форму многугольника, но и его положение на плоскости. Положение задается 3 координатами(например, пара координат одной вершины и угол поворота многугольника вокург нее). Таким образом, получается система с 2n-3 степенями свободы, в то время как длины ребер накладывают лишь n условий, и при n>3 получается 2n-3>n. Говоря математическим языком, иммется n функций от 2n-3 переменных, сопоставляющие набору координат вершин набор квадратов длин ребер(берутся квадраты, чтобы функции получились полиномиальными) и при n>3 образ функции далеко не однозначно задает прообраз.

Проведем теперь аналогичное вычисление для многогранников. Форма многогранника с n вершинами задается 3n-6 параметрами(так как полжение многогранника в пространстве задается 6 параметрами). Посчитаем теперь количество ребер. Пусть их число равно e. Если f — число граней, то 3f=2e, так как к каждому ребру прилегают две грани, а каждая грань содержит 3 ребра. Применяя Формулу Эйлера ^[4], получаем n-e+2e/3=2, то есть e=3n-6. Получается, что число условий, накладываемых на многогранник в точности равно числу степеней свободы.

Это не означает, что длины ребер однозначно задают форму многогранника. Вполне возможно, у каждого набора длин ребер будет несколько прообразов среди форм многогранников, но они будут изолированными(как в примере в начале поста), но локально прообраз единственен. См. Теорема о неявной функции ^[5]. Целое семейство прообразов, нужное для изгибания найдется только при условии вырожденности набора функций, см. Якобиан ^[6]. Таким образом, для возможности изгибания комбинаторная структура многогранника должна задавать вырожденную систему уравнений на длины ребер и координаты вершин, что объясняет редкость изгибаемых многогранников.

После построения примеров изгибаемых многогранников математики начали изучать их свойства при изгибании. В 1996 Сабитов открыл удивительный факт — изгибаемый многогранник сохраняет объем при изгибании(точнее, он доказал более сильное утверждение — объем многогранника является корнем многочлена, коэфициенты которого полиномиально выражаются через квадраты длин ребер). Что примечательно, несмотря на недавность результата, доказательство совсем не сложно и понятно студенту-математику 1-2 курса.

Далее математики стали изучать многогранники старших размерностей. А. Гайфуллин доказал аналог теоремы Сабитова во всех размерностях и построил примеры изгибаемых многогранников всех размерностей.

Дополнительные материалы:

1. Видео ^[7] на сайте etudes.ru об изгибаемых многогранниках
2. Статья И. Максимова ^[8] об изгибаемых многогранниках с малым количеством вершин
3. Лекция А.Гайфуллина ^[9]
4. Инструкция ^[10] по склейке многогранника Штеффена

Автор: aapetrov3

Источник ^[11]