Развлечения на плоскости Лобачевского

Евклидова плоскость скучна. Доступное пространство растет всего лишь как квадрат радиуса обзора. По сравнению с ней просторы плоскости Лобачевского гигантски. Но и там есть жизнь ^[1]!
Сумма углов многоугольника здесь меньше, чем у Евклида и не постоянна, а зависит от площади (от сюда интересное следствие — существуют самые большие треугольники, четырех- пяти- и тп угольники, сумма углов который становится равной нулю). По этому существуют замощения плоскости любыми правильными многоугольниками, если они достаточно велики. В статье про игру Жизнь используется замощение четырехугольниками, в каждой вершине сходятся по пять четырехугольников. Но такие четырехугольники очень велики. Если отказаться от одинаковости многоугольников, можно взять замощение из правильных шести- и семиугольников. Для него можно изготовить наглядную модель плоскости из магнитных шариков «Неокуб».

Многоугольниками будут колечки из шести и семи шариков. Колечки можно соединять между собой. Если они одной ориентации (направлению магнитного поля в кольце), они сцепляются ребрами из двух шариков, если разной — ребром с вершиной. Каждый семиугольник соприкасается с семью шестиугольниками.

Каждый шестиугольник — с тремя семиугольниками и тремя шестиугольниками.

Небольшой фрагмент плоскости начинает собираться в складки, при дальнейшем росте угожить в раще пространство его уже не получается. Но можно вырезать полоску равной ширины (ограниченную не прямыми, а гиперциклами ^[2]), то ее можно свернуть в спираль.
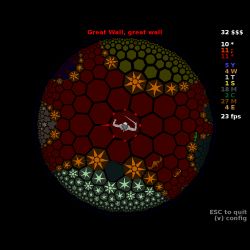
Компьютер не столь сильно ограничен геометрией реального пространства и погулять по плоскости Лобачевского можно в hyperrogue ^[3]. Поиграв в эту игру можно почувствовать некоторые особенности гиперболической геометрии. Местный вариант теоремы Пифагора записывается так: ch(с)=ch(a) ch(b) (через ch обозначается гиперболический косинус ^[4]). При малых значениях длин он превращяется в обычную теорему Пифагора (в этом легко убедится, разложив ch в ряд Тейлора до второй степени). При больших (ch становится почти равным половине экспоненты) — гипотенуза приближается к простой сумме катетов. То есть бежать наперерез больщого смысла не имеет и убегать становится проще, чем догогять. Длина окружности стремится к экспоненте радиуса — обходить препятствия получается очень долго.
К сожалению, стратегических игр на плоскости Лобачевского я не нашел. Так как периметр и площадь фигур растет примерно одинакого, контроль большой территории не будет давать серьезного преимущества в обороне границ. А так как площадь круга растет экспоненциально, можно было бы компактно размещать огромные армии. По моему, это сделало бы игру интереснее.
Жаль, что геометрия нашего мира в обозримом масштабе не гиперболическая…

Автор: potan

Источник ^[5]