Анализ агломерации ассоциированных систем

Допустим, Вы занимаетесь молекулярным моделированием. На руках у Вас имеются громоздкие файлы траекторий, которые неплохо было бы как то проанализировать. Рассмотрим (и ниже пойдет речь, в основном, именно об этой системе), например, метанол. Мы можем, к примеру, построить функцию радиального распределения (RDF), как это делается почти в каждой подобной статье. Но, вспоминая о том, что в метаноле существует специфическая агломерация — водородные связи — мы можем вдруг захотеть посмотреть, а как же оно там все выглядит на самом деле. Посмотреть, как выглядят агломераты (может даже сравнить их топологию), как распределяются они по размеру или еще, что захотите. Собственно ниже я предлагаю один из вариантов реализации подобной программы.

Немного теории

Первое — не важно, каким методом Вы получили траектории файлов — хоть QM, хоть MM, хоть гибрид какой. Важно то, что Вы должны знать точные координаты атомов. Даже не принципиально, чтобы это была траектория — можно использовать один снимок траектории, но от этого пострадает статистика и, как следствие, полученные результаты могут быть неправильны.

Теперь обратимся к вопросу, связанному с определением водородной связи. Наличие (или отсутствие) водородной связи предлагается определять несколькими возможными способами (а также, их комбинациями), например:

• Расстояния между атомами кислорода разных молекул и атомом водорода и атомом кислорода другой молекулы должны быть меньше референсных значений
• Расстояния между атомами кислорода разных молекул и угол HOO должны быть меньше референсных значений
• Энергетический критерий

Последний критерий не слишком удобен, по причине того, что во-первых, он гораздо более ресурсозатратен, во-вторых, трудно определить референсное значение энергии, ну и в-третьих, требуются дополнительные данные (если, например. считать их взаимодействие, как ван-дер-ваальсовое, то необходимо задать еще два параметра для каждого атома (положение минимума на поверхности потенциальной энергии и его глубину). Первый и второй критерий, по сути, являются эквивалентными — треугольник OHO можно задать как по трем сторонам (первый критерий), так и по двум сторонам и углу между ними (второй) — следует заметить, что внутримолекулярная связь O-H задана по условию задачи. В дальнейшем, я буду использовать только первый критерий по причине его удобности и наглядности.

А что нам нужно учесть?

Как известно, современные ресурсы не позволяют моделировать громоздкие системы (а-ля элементарная ячейка. содержащая 1 моль молекул), потому приходится использовать периодические граничные условия. Реальную бесконечную систему заменяют совокупностью одинаковых конечных систем, каждая из которых расположена в пространственной ячейке, окруженной со всех сторон тождественными ячейками, а молекулы, находящиеся в одной ячейке, взаимодействуют с молекулами в соседних. В реальности же, для подобного анализа, нам вовсе не обязательно транслировать ячейку во все стороны, увеличивая расчетное пространство в 27 раз (вместо одной ячейки получим 3^3=27). Можно ограничиться трансляцией на половину ребра в каждую сторону. Нетрудно показать, что в этом случае мы увеличим расчетное пространство всего в 8 раз. При этом, мы можем явно транслировать, забивая новые координаты в переменные, или же просто «иметь в виду» возможность трансляции при анализе. В моей программе реализован первый вариант. При этом, кстати, следует учитывать, что связь с молекулой в оттранслированной ячейке должна переноситься на молекулу в оригинальной ячейке.

Второй вопрос, с которым мы можем столкнуться — а что, если у нас имеется молекула с двумя функциональными группами? Например, для водородных связей — этандиол. Или еще веселее — вода. Такую возможность я предлагаю учитывать вводя дополнительную метку — номер молекулы. То есть оперировать не отдельными группами, а молекулами сразу.

Третья проблема — подобную агломерацию можно наблюдать не только в системе с OH-группами, но и, например, в хлорбензоле. Я не буду вдаваться в подробности, что, как и почему, замечу только, что подобная ассоциация аналогична мицеллообразованию в коллоидных системах. В таком случае, мы можем анализировать расстояния хлор-хлор для определения, являются ли молекулы связаны в ассоциат.

Реализация

Сделаю сразу пару замечаний. Программист из меня кривой чуть более, чем полностью, потому что-то, наверняка, можно сделать лучше. Сначала думал привести блок-схему, но она получалась какая-то слишком уж громоздкая.

Исходные данные:

• Координаты интересующих нас атомов (в т.ч. оттранслированных), в примере с метанолом — атом кислорода и связанный с ним водород
• Массив меток, обозначающий к какой молекуле относятся те или иные функциональные группы
• 2 параметра — референсные межмолекулярные расстояния O-H и O-O

Алгоритм поиска связанных молекул:

1. Два вложенных цикла с итерацией по всем молекулам (в том числе и оттранслированными) -второй цикл, естественно, начинается со следующей молекулы (зачем нам одно и то же по два раза учитывать?).
2. Считаем расстояние между атомами кислорода.для всех групп в молекулах, находим среди них минимальное. Проверяем с референсным. Если меньше, то идем дальше.
3. Реализация предыдущего шага, но уже для атомов кислорода и водорода. То есть, считаем все возможные (если на одном кислороде, к примеру, два водорода — как в воде) расстояние между атомами кислорода первой молекулы (определенного на предыдущем шаге) и водорода второй молекулы (связанного с кислородом, определенным на предыдущем шаге), находим минимальное. Проверяем с референсным. Если меньше, то идем дальше. Если больше, то сначала проверим обратный вариант — расстояние между атомами водорода первой молекулы и кислорода второй молекулы. Если меньше, то идем дальше, больше — идем к следующим молекулам.
4. Записываем, что эти молекулы связаны (при необходимости и длины связей тоже), переходим к следующим. При этом все связи с транслированных молекул записываем на молекулы, находящиеся в оригинальной ячейке.

Для случая одноатомного взаимодействия, например, в хлорбензоле, пункт 3 просто выкидывается.

Алгоритм вывода:

1. Ставим бинарную метку для каждой молекулы в оригинальной ячейке (т.е. без транслированных) в True. Цикл с итерацией по молекулам в оригинальной ячейке.
2. Берем первую молекулу с меткой True, ставим ей метку False. Записываем ее в массив агломератов, дальше записываем туда же все молекулы, которые имеют метку True и связаны с ней, приписывая им False. Продолжать до посинения тех пор, пока не будет новых связей.
3. Повторяем предыдущий пункт, пока у всех молекул не будет стоять метка False.

Затем выписываем массивы агломератов в любой удобной форме. В конце добавляем блок с общей статистикой (усреднее по всем точкам траектории). Можно дополнительно добавить статистику связей между, скажем, атомами кислорода.

А что бы еще добавить?

Первое — кросс-анализ на предмет наличия или отсутствия циклов в ассоциате. Не вдаваясь в доказательства, замечу, что. если молекуле, связанной с одной молекулой присвоить вес 0, с двумя -1 и т.д., а затем посчитать полный вес графа (ассоциата), то можно определить число циклов в графе:

• Если вес P графа равен N-2, где N — число вершин графа (молекул в агломерате), то граф не имеет циклов и имеет либо разветвленную, либо линейную структуру
• Если вес P графа больше N-2, то граф имеет циклы в количестве (P-N)/2+1

Второе гораздо веселее. Есть оригинальные статьи — тут ^[1] и тут ^[2]. Смысл в том, что если мы имеем два графа, то можем сравнить, являются ли они изоморфными (в смысле одинаковыми ± перестановки) и определить перестановку, по которой один граф из другого получается. Правда, если мне не изменяет память, в этих статьях были опечатки в самих алгоритмах, будьте внимательны.
Применительно к нашей системе — мы можем создать базу данных основных графов и проверять полученные ассоциаты на соответствие определенному графу. Также, можно провести и статистику.
К сожалению, этот блок я не реализовывал. В наличии имеется только программа, проверяющая два графа на изоморфность.

Ну и третье. Анализ одной молекулы — динамика нахождения ее в различных агломератах на всем протяжении траектории.

В дополнение

Исходные коды программ можно взять по ссылке ^[3]. Все реализовано на C. Комментариев в коде, к сожалению, нет.
Программа STAT_GEN работает с форматом файлов, похожих на файлы траекторий TINKER'а за одним исключением — нет блока, отвечающего связанности различных атомов друг с другом, и добавлен столбец, обозначающий номер молекулы.
Программа AGL выдергивает отдельные агломераты из траекторных файлов и записывает их в формат PDB.
Программа graph анализирует изоморфность графов.
К сожалению, работоспособность этих программ на Windows после переноса на LInux (изначально писалась под винду, потому там есть, например, библиотека conio.h) проверена не была, потому не знаю, что там да как.

На выходе можно получить что-то вроде такой картинки (с одной из моих презентаций):

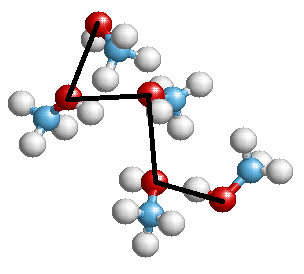
Или другая структура, в виде графа:

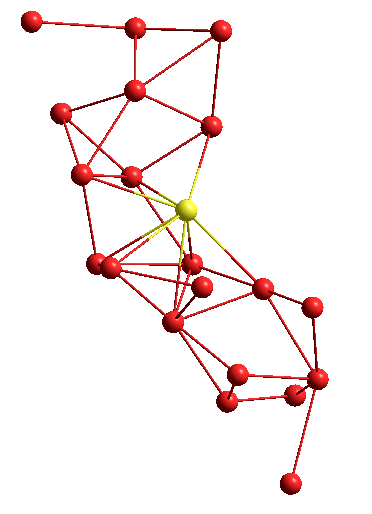
Спасибо за внимание!

Автор: arcan1s

Источник ^[4]