Пятничные клеточные автоматы: 10 правил «больших, чем жизнь»

👾!

Осторожно, присутствует несколько мерцающих анимаций. Они спрятаны под спойлеры, открывайте на своё усмотрение. На большом экране рекомендуется смотреть в хорошо освещённом помещении.

Неделю назад мы сделали шаг в сторону нетоталистичных конфигураций ^[1], где считали не только количество, но и расположение живых соседей. Сегодня шагнём в другую сторону от тоталистичных правил – увеличим радиус поиска соседей.

Самое популярное подобное расширение известно как Larger than Life, или просто LtL. Данная конфигурация была описана в докторской диссертации профессора Калифорнийского университета – Келли Мишель Эванс (Kellie Michele Evans) в 1996г., и нередко название конфигурации дополняется именем автора.

Нотация

В общем виде расширение предполагает указание следующих параметров:

• Диапазон количества соседей для выживания клетки;

• Диапазон количества соседей для рождения клетки;

• Радиус поиска соседей;

• Количество поколений (в данной конфигурации чаще называемых «состояниями»);

• Тип окрестности (чаще всего это окрестность Мура или фон Неймана );

• Учёт центральной клетки в счётчике соседей.

Последнее, небольшое, но значимое дополнение, является новым в нашей серии, и в рассматриваемых ранее конфигурациях этот пункт всегда принимался как M0, то есть состояние само́й клетки не включалось в общий счётчик.

В классическом виде нотация выглядит следующим образом:
Радиус поиска соседей</p>" data-abbr="Rr">Rr,Количество состояний (поколений)</p>" data-abbr="Cc">Cc,Учёт центральной клетки (0 или 1)</p>" data-abbr="Mm">Mm,SДиапазон количества живых соседей для выживания (включая верхнюю границу)</p>" data-abbr="smin..smax">s_{Диапазон количества живых соседей для выживания (включая верхнюю границу)</p>" data-abbr="smin..smax">min}Диапазон количества живых соседей для выживания (включая верхнюю границу)</p>" data-abbr="smin..smax">..s_{Диапазон количества живых соседей для выживания (включая верхнюю границу)</p>" data-abbr="smin..smax">max},BДиапазон количества живых соседей для рождения (включая верхнюю границу)</p>" data-abbr="bmin..bmax">b_{Диапазон количества живых соседей для рождения (включая верхнюю границу)</p>" data-abbr="bmin..bmax">min}Диапазон количества живых соседей для рождения (включая верхнюю границу)</p>" data-abbr="bmin..bmax">..b_{Диапазон количества живых соседей для рождения (включая верхнюю границу)</p>" data-abbr="bmin..bmax">max},Тип окрестности (m – Moore; n – von Neumann)</p><p></p>" data-abbr="Nn">Nn

В будущих статьях мы коснёмся конфигурации, где допускается множество диапазонов для рождения и выживания клетки, однако в рассматриваемой сегодня указывается только по одному диапазону для каждого параметра.

Параметры окрестности и учёта центральной клетки могут быть опущены в записи правила. В этом случае, в качестве стандартных значений для них принимаются NM – окрестность Мура, и M0 – без учёта центральной клетки. Поколения, как и ранее, тоже можно опустить, подразумевая G2.

Нотация предлагает использовать C для обозначения поколений (Count of states) и запятые в качестве разделителей. Это не совсем согласовано с прочими нотациями, потому мы будем использовать привычные G и /.

В качестве разделителя в диапазонах, в разных вариантах нотации может использоваться двое- и троеточие, дефис и t (to).

0. Жизнь

Для гарантии, что наша симуляция работает правильно, давайте реализуем классическую «жизнь» Конвея в рамках LtL.

Отлично, кажется, всё работает как и должно.

А что, если мы немного изменим правило? К примеру, будем учитывать центральную клетку?

Совершенно другая картина. Состояние за первый десяток итераций приходит к виду с простейшими натюрмортами и осцилляторами.

Можно подумать, что если мы уменьшим S, то вернём правило к известному виду. Но это не так:

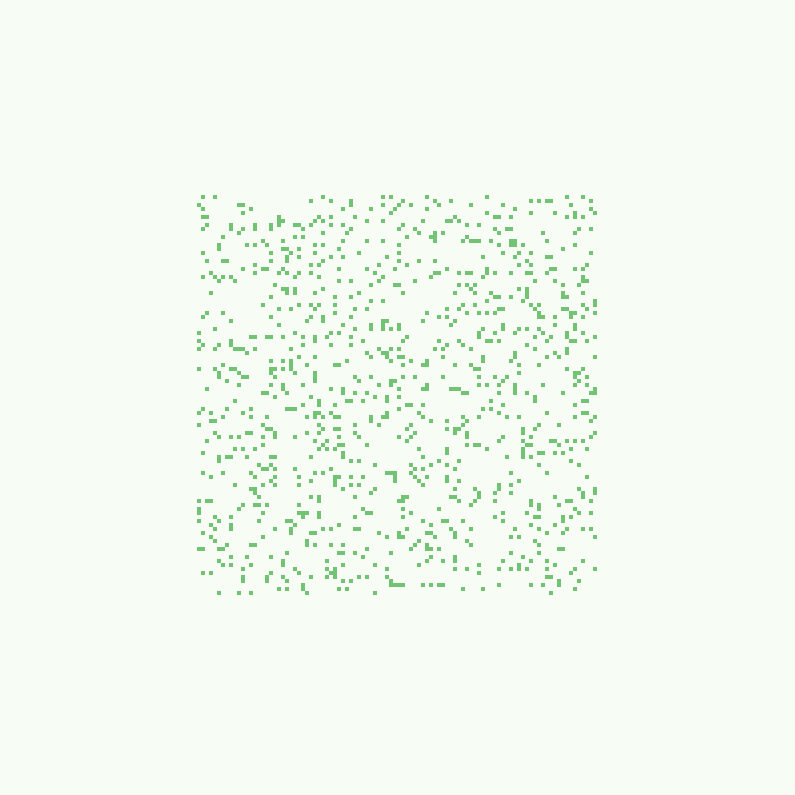
Поэтому данный параметр вынесен отдельно, а в англоязычной традиции «life-like» конфигурацию называют outer-totalistic, то есть "учитывающую только внешние клетки".

1. Bugs

В именованных правилах LtL конфигурации очень много «жуков».

Первое подобное правило было описано самой Келли Эванс, и известно также как «Bosco's rule», по названию, которое было дано часто осциллятору с большим периодом (от 166 итераций), вариации которого и порождают «жуков».

Копошиться сегодня будем, в основном, на нецикличной сетке 300×300.

Bosco's rule – R5/G2/B34-45/S33-57

Bugs 3R – R3/B14-18/S14-23

Bugs R7 – R7/B63-84/S63-108

Bugsmovie – R10/B123-170/S122-211

Miniature Bugs – R3/B14-25/S15-22

... и ещё бесчисленное множество подобных им. Можно сказать, что жуки являются естественными обитателями LtL конфигурации.

2. Globe

На разрастающихся правилах большой радиус может давать интересные окаймовки, как зубцы у этого правила.

R8/G2/B74-252/S163-223

3. Liquid methuseblob soup

Перетекающие правила всегда смотрятся интересно, а данное же ещё дополняется определённой внутренней структурой. Также занимательно, что направление роста можно определить даже по отдельному фрейму по толщине берега.

R6/M1/B52-60/S58-90

4. R7/B72-99/S72-225

Орнаменты с финальным видом на LtL конфигурации редко находятся, разве что на неумирающих правилах.

Конечно, определённой симметрии можно добиться и с заготовленными стартами на других правилах:

R10/M1/B3-3/S2-3

5. Modern Art

Демонстрацию данного правила пришлось хорошо порезать. G255 по размеру никак не укладывались, оставил по 1 фрейму "роста" из 20.

R10/G255/B3/S1-2

Можем позволить себе изменить количество поколений. Результат, конечно, несколько изменится.

G10. Без обрезок.

6. R2/B7-24/S19-25

Одно из самых медленно растущих и необычных правил. Рост происходит одновременно двумя шаблонами – чередующимися "зеброй" линиями и "колючей проволокой", которая, искривляясь, проходит через линии, но почти не нарушает их, а накладываясь на прямые становится основным видимым шаблоном.

R2/B7-24/S19-25

Как и с прошлым правилом – полный вид не влезает по размеру. В конце он выглядит так:

7. R2/G5/B4-4/S3-3

Немного неожиданно, но простые и стабильные космические корабли – редкость для данной конфигурации, даже в единичных экземплярах. Слишком много возмущений вносит расширенный радиус. Потому привычные корабли можно увидеть только на самых строгих вариантах:

8. Pigs & R2/B4-4/S1-1

Примерно так же обстоит дело и с привычными, по прошлым конфигурациям, стабильными репликаторами и осцилляторями. Правила с ними выделяются на общем фоне.

9. Возмущения

Но они же и порождают правила, вроде таких:

10. R7/G5/B63-82/S64-109

Напоследок взглянем, как выглядит одно из бесчисленных правил с «жуками» в поколенческом виде:

Бонус. Extra range

R45/G2/B2500-4973/S2884-4922

---

Читайте также

• 🟢10 зрелищных клеточных автоматов с поколениями ^[2]

• 🟢10 удивительно зрелищных простейших клеточных автоматов ^[3]

• 🟢 История моделирования лесных пожаров ^[4]

• 🔵 Моделирование лесных пожаров: теория, клеточный автомат на Python ^[5]

• 🟠 Сегрегация общества: модель Шеллинга и распределение этнических групп в городах Израиля ^[6]

← Предыдущая часть ^[1]