Удивительные клеточные автоматы: блочные КА, окрестность Марголуса

👾!

Сегодня мы снова ^[1] немного отойдём от классической модели, и будем строить конфигурацию с самого начала, благо, никаких сложностей в этом нет. Сегодняшняя конфигурация – блочные КА – предполагает, что наша сетка разбивается на некоторые участки, собственно, блоки, для которых заранее определены инструкции перехода. Никаких вариаций – один шаблон перехода для одного шаблона расположения. Звучит так, будто мы получим набор бессвязных осцилляторов, верно? Но у конфигурации есть второе условие: каждый шаг происходит смещение сетки разбиения, за счёт чего клетки при каждой следующей итерации относятся к новому блоку. Лучше, конечно, на примере.

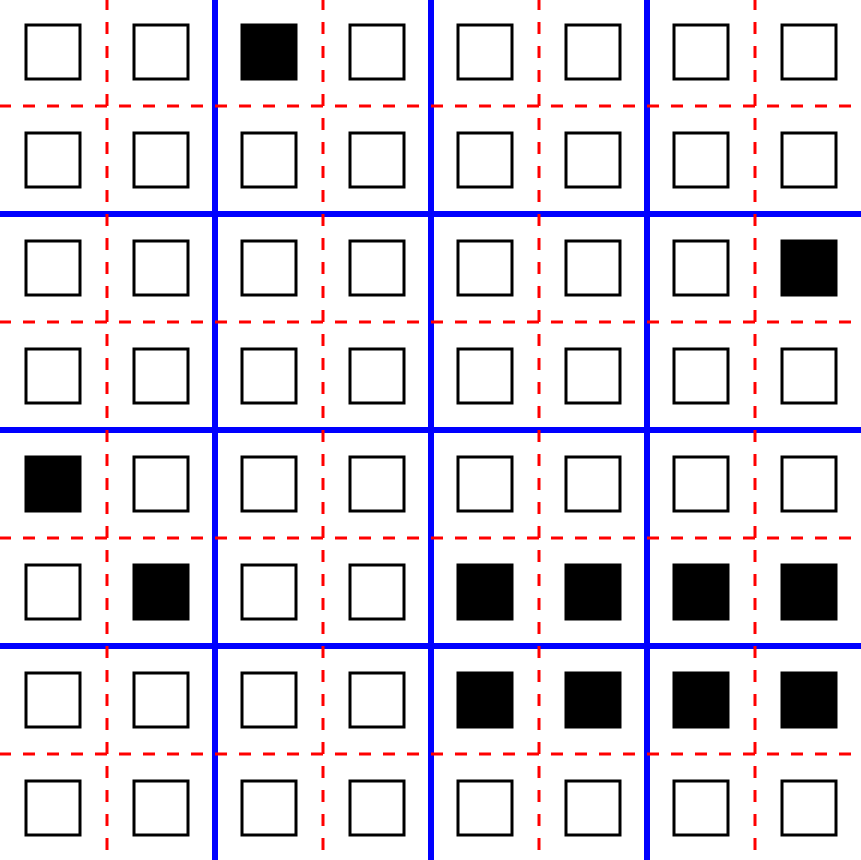
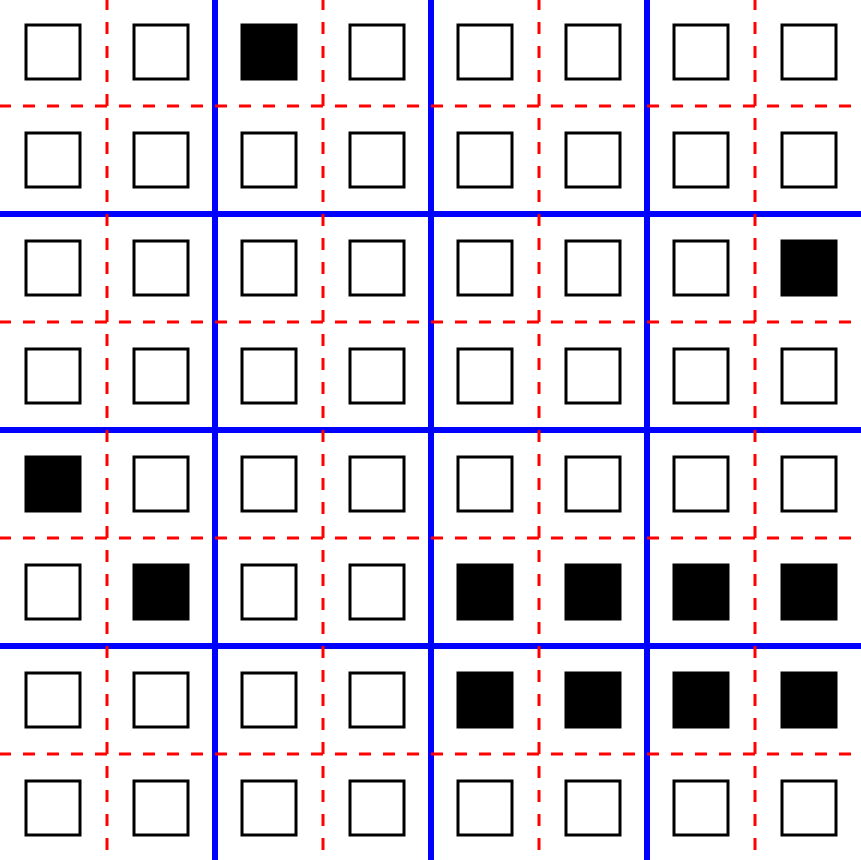
^{Синими линиями формируются блоки на чётных итерациях, красными пунктирами – на нечётных}

Как и в случае с альтернативными окрестностями, данный раздел КА также весьма скудно исследован (данное утверждение будет становиться только актуальнее, чем дальше мы будем отходить от стандартной модели), и окрестность Марголуса является чуть ли не единственной признанной на всей конфигурации. Тем не менее, это не значит, что нам не найдётся на что посмотреть.

❯ Вводная

В общем виде, каждое правило вида содержит в себе некоторое количество инструкций перехода в одномерном представлении, вроде 0, 0, 0, 0: 1, 1, 1, 1 (=блок со всеми пустыми клетками становится полностью заполненным).

Кроме набора инструкций также уточняется, нужны ли повороты инструкций и их отражения по горизонтали и вертикали. Это позволяет сократить описания, например, сделав эквивалентными 1, 0, 0, 0: 0, 1, 0, 0 и 0, 1, 0, 0: 1, 0, 0, 0 горизонтальным отражением.

Также, для сокращения количества описываемых инструкций, отдельные значения клеток могут быть заменены переменными, то есть принимать любое значение.

Пример: 0, 0, 0, 0: 0, 0, 1, 1 и 1, 0, 0, 0: 1, 0, 1, 1 заменяются на a, 0, 0, 0: a, 0, 1, 1

Стоит упомянуть, что блочные КА являются обратимыми, то есть мы, зная текущее состояние поля и инструкции перехода, можем шаг за шагом восстанавливать предыдущие состояния.

❯ 1. Бильярд

Начнём с не самого простого примера, но на нём мы хорошо закрепим понимание данной конфигурации. Billiard Ball Machine.

Правило определено двумя переходами с поворотной симметрией, и, как и большинство правил конфигурации, требует определённого стартового состояния.

Симметрия: поворот
1, 0, 0, 0: 0, 0, 0, 1
1, 0, 0, 1: 0, 1, 1, 0

^{18с., скорость 3, 112×112}

У вас может возникнуть вопрос – «А почему «шары» правильно рикошетят? Мы ведь не задаём никакого направления, известно только текущее состояние». Секрет во второй инструкции, и в том, что наши «шары» состоят из двух клеток. Немного замедлим анимацию:

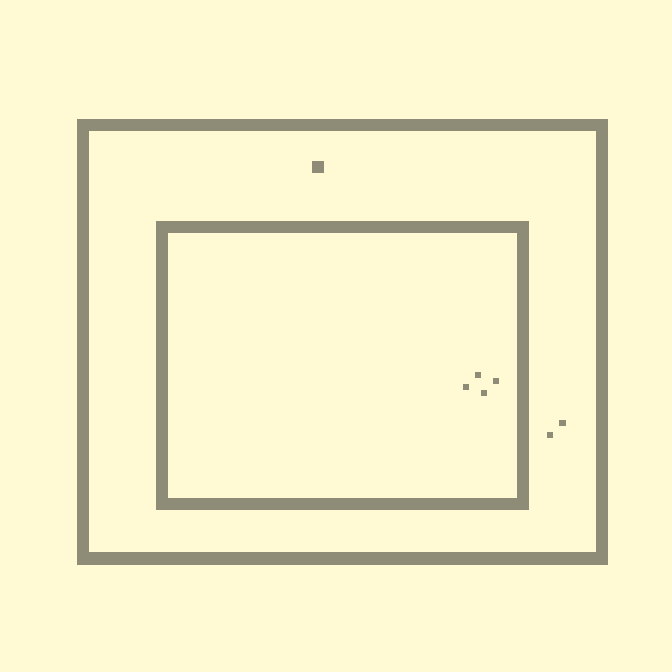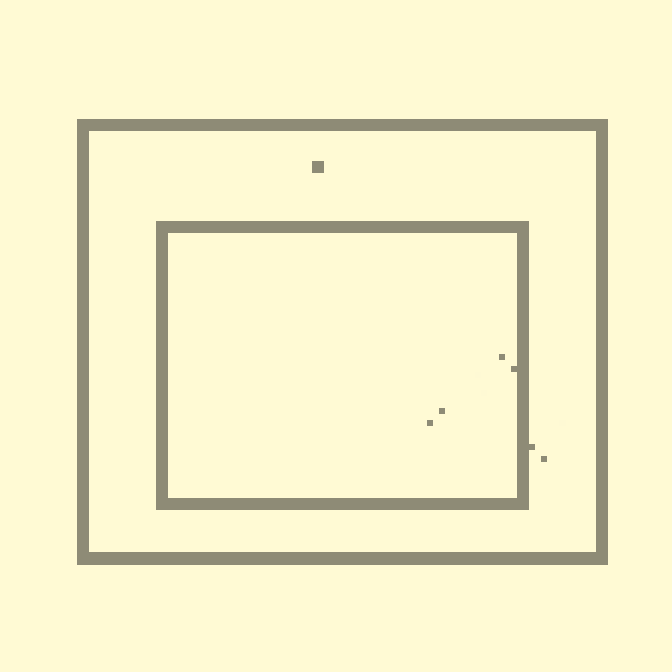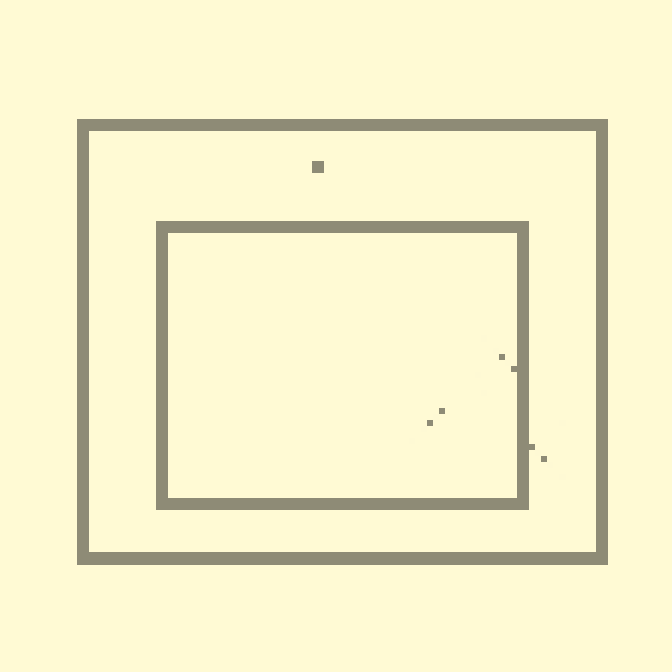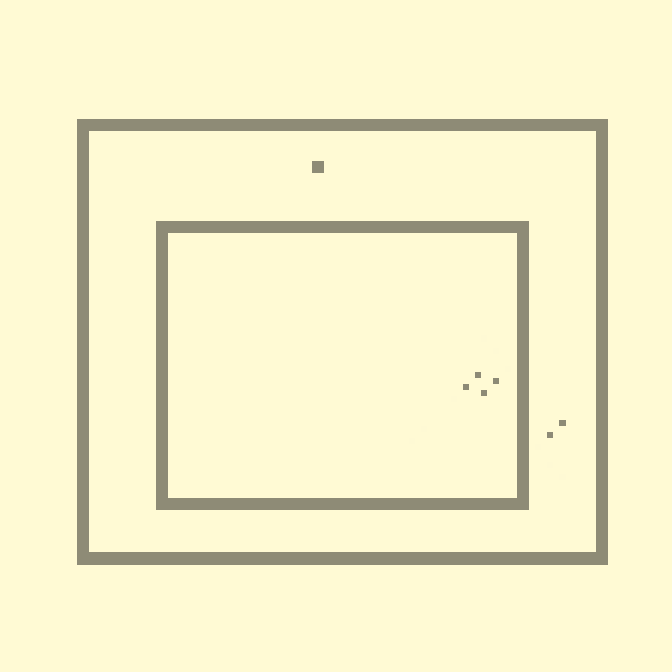
^{10с., скорость 0.2, 112×112}

Давайте нарушим стартовое состояние: внешний шар сдвинем на одну клетку выше, у первого внутреннего уберём одну клетку, а для второго шара придвинем клетки ближе друг к другу.

^{12с., 112×112}

Всё, ожидаемо, сломалось. Возможно, у вас возник новый вопрос – «Хорошо, а почему отдельные клетки вообще отскакивают в ту же сторону, откуда и прилетели?».

Тут суть в самой конфигурации – клетка, которая изменилась по переходу 1, 0, 0, 0: 0, 0, 0, 1 не может оказаться в другом блоке на второй или третьей позициях, она всегда будет на позициях 1 и 4, и будет следовать переходам по этой диагонали. И наоборот – клетка на позициях 2 и 3 по этому переходу (Симметрия: поворот) всегда будет на них же.

Обилие линий на изображении окрестности может скрыть от вас эту контринтуитивную особенность, которая является крайне важной при реализации алгоритма и составлении фигур. Взгляните на изображение ещё раз (продублировано ниже, под спойлером). Из-за того, что мы с каждой итерацией смещаемся по диагонали, блоков со стартовыми клетками на позициях x+1 или y+1 попросту не существует. Другими словами, существуют только те блоки, у которых сумма позиций по обеим осям у стартовых клеток чётная.

 

Что же, можно считать, что мы разобрались с конфигурацией. Теперь можем насладиться прочими примерами.

❯ 2. Песок

Одно из самых популярных правил конфигурации моделирует поведение клеток-песчинок, пусть и с некоторыми допущениями.

Симметрия: отражение по горизонтали
1, 1, 0, 0: 0, 0, 1, 1
1, a, 0, b: 0, a, 1, b
1, 0, a, 0: 0, 0, a, 1
3, a, 0, b: 3, a, 1, b

В данном правиле предполагается 4 состояния: 0 – пустая клетка; 1 – песчинка; 2 – неподвижные клетки, которыми мы можем создавать поверхности для песка; 3 – бесконечный источник песка.

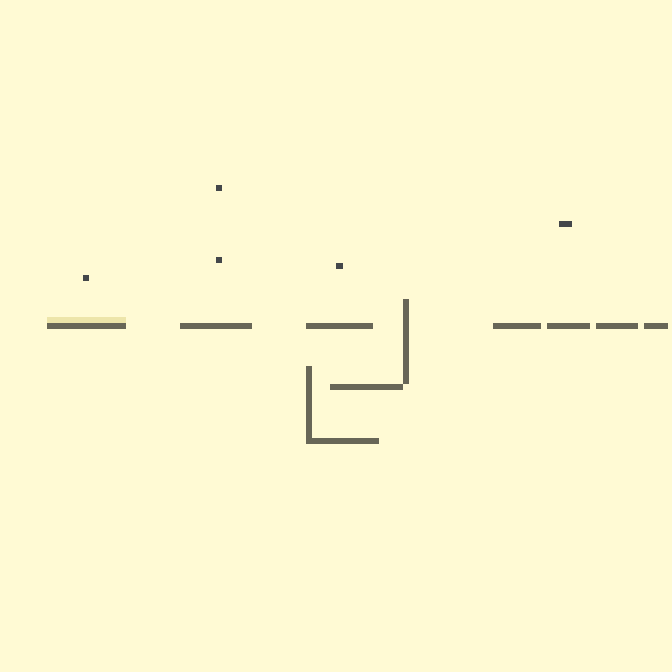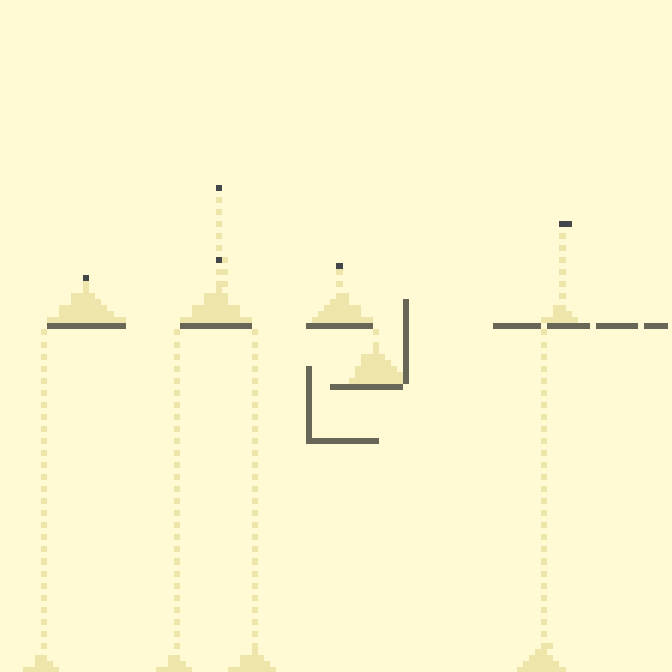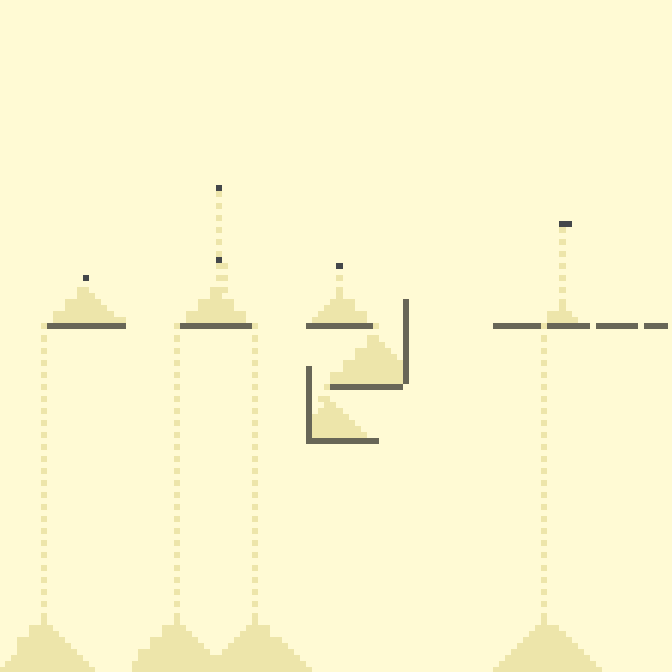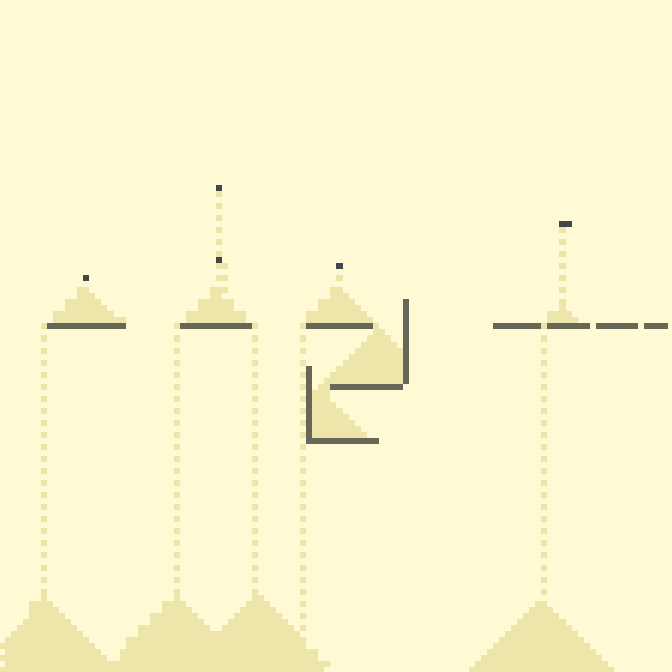
^{40с., скорость 1.5, 112×112}

Здесь видна основная масса допущений, однако даже с ними, модель весьма близка к своему прототипу.

С бо́льшим количеством песчинок можно обнаружить ещё одну занятную особенность, когда клетки при падении собираются в линии.

^{28с., скорость 1.5, 224×224; Случайное заполнение (20%)}

❯ 3. Diffusion Limited Aggregation

Симметрия: отражения + поворот
1, 0, 0, 0: 0, 0, 0, 1
1, 1, 0, 0: 1, 1, 0, 0
0, 1, 1, 0: 1, 0, 0, 1
1, 1, 1, 0: 1, 1, 0, 1
1, 0, 2, 0: 2, 0, 2, 0
1, 0, 2, 2: 2, 0, 2, 2

Переходы для состояния 1 могут напомнить бильярдное правило, с парой модификаций:

^{13с., 112×112; Случайное заполнение (5%)}

Но основной интерес к правилу вызывают клетки во втором состоянии, благодаря которым возникает рост, схожий со многими природными процессами:

^{32с., 112×112; Случайное заполнение (60%) + центральная клетка во втором состоянии}

❯ 4. Toothpick sequence

Одно из простейших правил, с единственным переходом: в каждом блоке, с единственной заполненной клеткой, также заполняются и смежные.

Симметрия: поворот
1, 0, 0, 0: 1, 1, 1, 0

^{15с., 224×224; Две стартовые клетки по диагонали}

❯ 5. Tron

Классическое правило конфигурации. Инструкции перехода ещё проще «зубочисток» – все пустые блоки заполняются, и наоборот. Никакие симметрии, конечно, не понадобятся.

Правило очень мерцающее, поэтому на анимациях убран каждый второй фрейм. Оригинальный вид оставим под спойлером.

^{15с., 112×112; Заполненный центральный блок 27×27}

^{57с., 224×224; Заполненные блоки 6×6, 2×2 и 2×2}

Поведение, которое можно видеть на границах примера, вызвано нецикличной сеткой. Если связать границы, вид существенно изменится:

^{25с., 224×224}

❯ 6. Криттеры

Развитие инструкций Tron'а привело к появлению правила Critters, интересного своими планерами.

Симметрия: поворот
0, 0, 0, 0: 1, 1, 1, 1
0, 0, 0, 1: 1, 1, 1, 0
0, 1, 1, 1: 1, 0, 0, 0
1, 1, 1, 1: 0, 0, 0, 0

Планеры на этом правиле очень устойчивы. Они могут проходить друг через друга без повреждений, с разным смещением, менять направление полёта, а если и будут повреждены, могут восстановиться следующим столкновением. Так как в основе лежат правила Tron'а, анимация опять мерцающая, и опять сокращена вдвое.

^{56с., 224×224, 50×40%}

❯ 7. Rotations

Ещё одно простое правило, порождающее «путешественников».

Симметрия: поворот
1, 0, 0, 0: 0, 1, 0, 0

^{59с., 112×112}

❯ 8. M0,2,8,12,1,10,9,11,4,6,5,14,3,7,13,15

Под конец познакомимся с ещё одним вариантом описания переходов.

Для блочных КА с двумя состояниями, расположения могут быть представлены как бинарные числа и в этом случае может использоваться упрощённая запись M0,1,2,…,14,15, где индекс обозначает изначальное расположение, а значение по индексу – шаблон расположения после перехода. Например M15,1,2,…,14,15 будет соответствовать правилу с единственной инструкцией «все пустые -> все заполненные», без обратного перехода.

Этот вариант достаточно компактен, но, к сожалению, не универсален.

Вернёмся к правилу. M0,2,8,12,1,10,9,11,4,6,5,14,3,7,13,15. Как вы видите, всего два значения остались на своих позициях, а остальная часть изменилась. В явной записи с сокращением симметрией это бы выглядело следующим образом:

Симметрия: поворот
1, 0, 0, 0: 0, 1, 0, 0
1, 1, 0, 0: 0, 0, 1, 1
0, 1, 1, 0: 1, 0, 0, 1
1, 1, 1, 0: 1, 1, 0, 1

На этом правиле можно найти много разных любопытных фигур.

^{17с., скорость 5, 112×112}

^{12с., скорость 3, 224×224}

❯ 9. M0,14,13,0,11,0,0,0,7,0,0,0,0,0,0,0

Занимательное правило, как по виду, так и по переходам: мы сохраняем переходы всего для четырёх расположений с одной заполненной клеткой, инвертируя состояние блока, и сбрасываем все остальные расположения к пустым блокам. Ну а в результате получаем орнаментно-фрактальные виды, с большой зависимостью от стартового состояния.

^{33с., 672×672}

^{30с., 672×672}

^{27с., 672×672}

❯ 10. M0,1,2,3,4,10,6,11,8,9,5,13,12,14,7,15

И закончим сегодняшний обзор занятным колебательным правилом.

^{35с., 112×112}

Другие фигуры, конечно, тоже возможны.

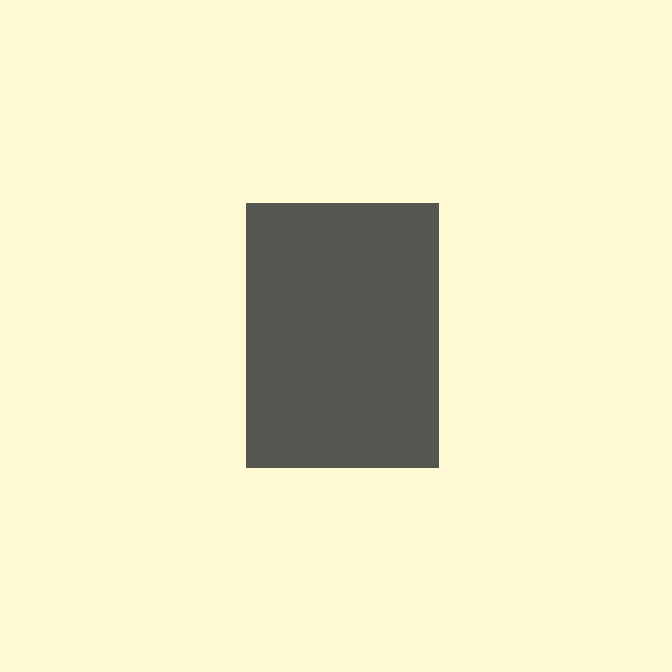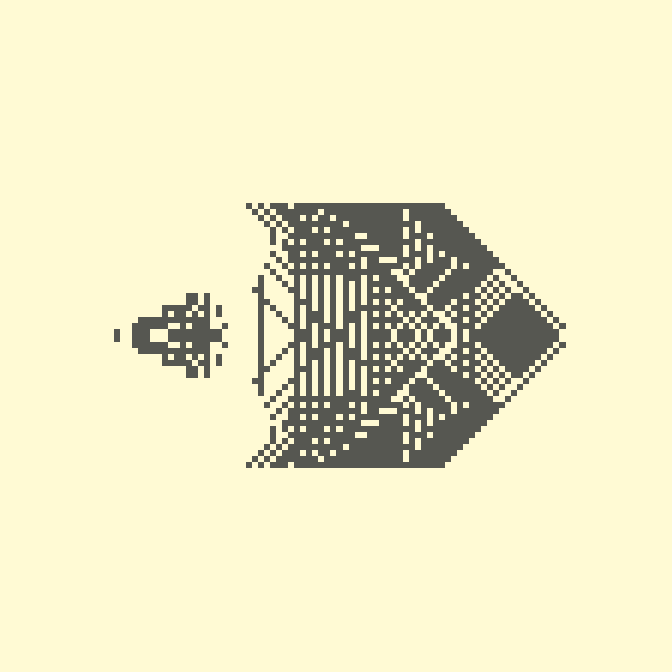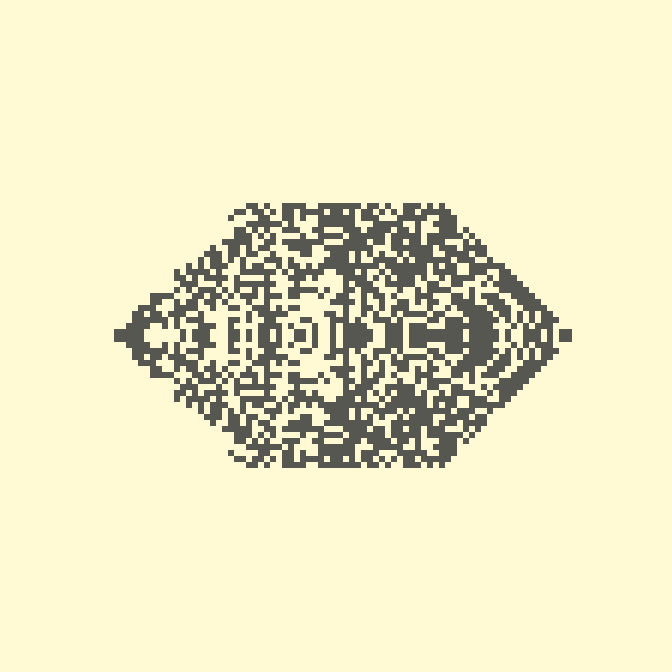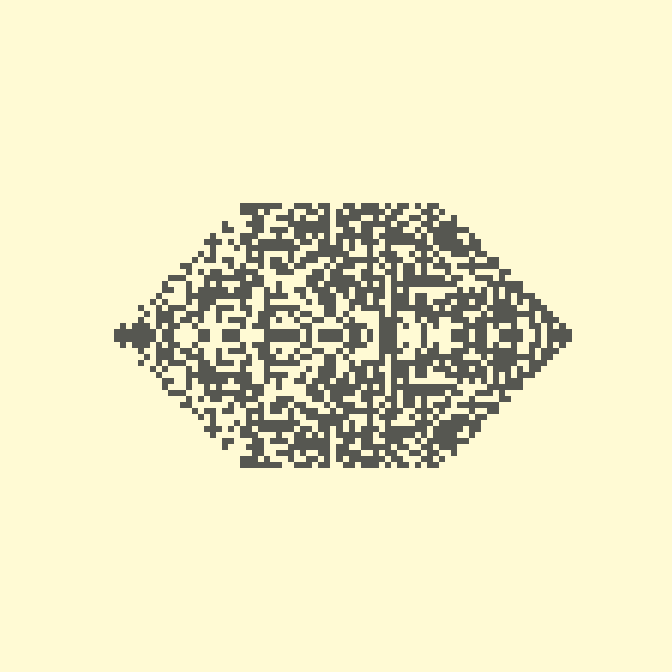
^{21с., 112×112}

---

И на сегодня всё. Увидимся через неделю!