На данном скриншоте Вам представлена, казалось бы, обыкновенная игра с пиксельной графикой. Однако не все так просто.

Рельеф земли местами напоминает синусоиду, а пули похожи на два симметричных графика корня из x.

На самом же деле, все что вы видите на экране так или иначе относится к математике, математическим кривым и графикам.

Предыстория

Как-то раз, просматривая видео канала «Numberphile», я наткнулся на очень интересный видеоматериал, под названием «Формула всего» ^[1].

В данном видеоролике была представленна самореферентная формула Таппера ^[2], которая при неком значении k, воссоздавала свое изображение на графике. Выглядит данная формула вот так:

Данная формула очень заинтересовала меня, и у меня появилась идея:

«А что если создать игру, где вместо обыкновенных текстур, которые хранятся в различных файлах .png и .jpg формата, будут использоваться математические графики, кривые?»

Мне данная идея показалась довольно интересной и непростой в реализации.

Задачи

Передо мной стояли следующие задачи:

• Придумать смысл игры, геймплей
• Вывести формулы, графики которых будут представлять собой нужные мне силуэты персонажей, пуль, поверхностей
• Реализовать все это в игре

Геймплей и смысл игры

Геймплей и смысл игры менялся несколько раз по ходу разработки данной игры. Это все потому, что возникали некоторые трудности, в частности, с выведением формул для определенных силуэтов. Но в целом, данная игра об одинокой летающей тарелке, которая летает по планетам, исследуя их и убивая врагов, которые встают у нее на пути.

Формулы и последующая их реализация в игре

Следующие два пункта я объеденил в один подзаголовок, потому что «скакать» между одной формулой и её реализацией нецелесообразно.

Для создания игры был выбран язык программирования c++ и библиотека SFML, для создания окон и отрисовки на них чего-либо.

Так как я учусь в школе и только недавно узнал о том, что такое синусоида и как она выглядит, у меня возникали довольно большие проблемы с выведением различных формул. Чаще всего это заканчивалось простейшим подбором.

В конце статьи будет ссылка на GitHub, где выложен весь код. В статье же будут приведены только маленькие кусочки кода, дабы не засорять её.

Поверхность планеты

Для поверхности планеты я вывел следующую формулу:

Довольно простая формула, но при реализации возникла потребность в управлении высотой и длиной данной синусоиды. Также, во избежании кривизны рельефа, x домножается на π. По этому, конечный код выглядит вот так:

int groundC = ceil(abs(sin(((i+1)*groundScale*M_PI)))*groundHeight);

Текстура планеты в космосе

Текстура планеты состоит из круга и узора на нем. В игре присутствует 4 формулы для создания узоров и 12 текстур планет с различным узором. В зависимости от «шага» формулы создаются различные узоры. Также, при генерации планеты, ей псевдорандомным ^[3] способом устанавливается цвет, размер и позиция в космосе.

Пули

Изображение пули из игры. Пуля повернута.

Для пуль была выбрана очень простая формула:

График данной формулы отзеркален по оси абсцисс.

Главный герой

Вот и добрались мы до самых сложных формул.

Формулу главного героя я вывел с большим трудом. Выглядит она так:

Да, очень кривая, очень некрасивая формула. Но главное не формула, главное результат.

Чтобы добиться результата, сначала я хотел просто двигаться по оси x с определенным шагом, записывать координаты y, и после соеденить все эти точки, получив тем самым нашу тарелку. Но потом, я случайно взял слишком маленький шаг, и у меня красиво вырисовалась вся тарелка за исключением двух конечных точек, которые в конце концов соеденялись. В итоге, тарелка выглядит так:

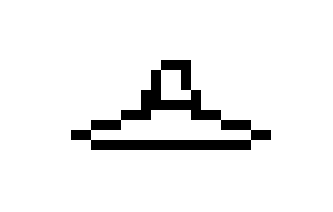
Далее нужна была текстура главного героя в космосе. Она выглядит так:

В её основу лег круг. Главная кабина выполнена с помощью следующей формулы:

График данной формулы отзеркален по оси ординат.

Вот так данная формула выглядит на c++:

int x = round(pow(pow(i, 7 - i), 0.8 / i));

Враги и их спаунер

Справа на изображении синий спаунер, красные объекты — враги.

Спаунер представляет собой обыкновенную планету с необыкновенным узором. Этот узор — график формулы:

Формула текстур врагов:

Деревья

Признаюсь, формулу для создания силуэта деревьев вывести либо подобрать я не смог. Но, дабы не нарушать основной концепт всей игры и правила не использовать любые файлы .png и .jpg формата, я воспользовался одной хитростью. Я использовал фракталы ^[4] для создания деревьев.

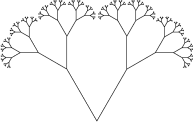
Пример фрактального дерева

Скорее всего вы согласитесь, что сами по себе фрактальные деревья выглядят достаточно скучно. Если добавить немного элементов случайности, например вырасти может не обязательно 2 ветки, но также 3 либо 1, либо вообще не вырасти. Также, можно сделать не везде одинаковый угол наклона.

Конечно, можно было бы сделать обыкновенный машинный псевдорандом ^[3], который основывался на тиках компьютера, но мне показалось более интересной следующая зaдумка:

«А что если выдать каждому дереву определенное число(сид), от которого будут высчитываться псевдо рандомные числа, влияющие на параметры дерева?»

К счастью, в c++ есть отдельная библиотека, отвечающая за псевдорандом.

В итоге, сгенерированные деревья выглядят вот так:

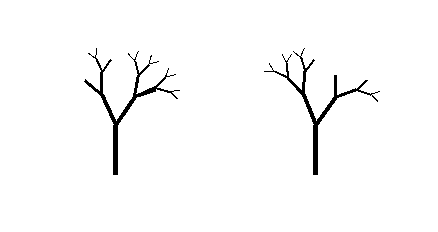
Слева находится дерево с сидом 13, а справа — 22

А код, генерирующий эти деревья так:

Branch Branch::createNewBranch(Branch cur, Tree* parent, float angleMultiplier, int level) {
	
  Vector2f sp(cur.startPoint.x, cur.startPoint.y);

  float randomAngle = ((*parent).getRand() * 15) - 5;

  float t = cur.thickness * 0.75;
  float l = cur.length * 0.67;
  float a = cur.angle + 30*angleMultiplier + randomAngle;
  sp.y -= (cos((cur.angle-180)*3.1415926 / 180) * cur.length);
  sp.x += (sin((cur.angle-180)*3.1415926 / 180) * cur.length);
  Branch gen(sp, t, l, a, level);
    if (level > 0) {
      int count = 100 * (*parent).getRand();
      if (count >= 25 && count < 80) {  //только после многочисленных тестов я заметил, что в этом месте пропустил && count < 80, по этому дальнейшие скрины могут иметь небольшие неточности, почти незаметные. Также, из-за этого пришлось понизить шанс не выростания одной ветки с 20% до 10%, по этому, в конечном коде count<90
	(*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1));
	(*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1));
      }
      if (count >= 80) { //как я уже объяснял раньше, в конечном варианте count >= 90
	if (count % 2 == 0) {
	   (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1));
	}
	else {
	   (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1));
	}
      }
    }

  return gen;
}

Примечание. Да, я знаю, что я «схардкодил» некоторые переменные, но прошу не винить меня в этом. Я посчитал, что не имеет смысла создавать отдельные константные переменные, которые впринципе влияют только на шанс создания новой ветки.

Еще немного кода

Выше я приводил код только для генерации текстур. В этом подзаголовке я опишу код самой игры. Весь код находится на GitHub'е, ссылка на проект в заключении. ^[5]

Игрок

У игрока есть два разных метода update — spaceUpdate и planetUpdate. Соответсвенно, spaceUpdate обновляет игрока, когда он находится в космосе, planetUpdate — когда на планете. На планете рассчитывается ускорение и скорость игрока. В зависимости он горизонтального ускорения меняется и угол наклона тарелки — от 30 градусов до -30. Приближаясь к барьерам скорость игрока уменьшается. Такие барьеры существуют для оси x(0; mapSize.x) и для оси y. Для оси y все чуть сложнее. Есть минимальная высота, которая рассчитывается так: берется минимальная высота земли, складывается с высотой синусоиды и еще прибавляется высота деревьев. Высота деревьев посчитана очень простым способом — начальная длина ветки умноженная на количество циклов, выполняемых при генерации дерева. Верхней границы нету — вылетая за карту сверху игрок переключается на spaceUpdate и отрисовывается космос.

SpaceUpdate действует следующим образом: рассчитывается ускорение и скорость игрока. Далее рассчитывается угол поворота игрока. Рассчитывается угол следующим образом: если ускорение равно нулю, то рассчитывается угол относительно скорости игрока, если же нет — относительно ускорения. Также, в космосе у игрока присутсвует возможность стрельбы. Стрельба происходит следующим образом — создается пуля с поворотом как у игрока и добавляется в список. При обновлении игрока в космосе, каждая пуля в этом списке также обновляется. При отрисовке игрока также отрисовываются и пули. Также, в космосе все немного сложнее с барьерами. Космос поделен на сектора, в каждом секторе по 4 планеты, всего — 1 000 000 планет и 25 000 секторов. У каждого сектора есть уникальный id. Если остаток при делении на 500 равен 0 — присутствует левый барьер, если остаток 499 — правый, если при делении на 500 результат равен 0 — пристуствует верхний барьер, если 499 — верхний. Если каких либо барьеров нету, то при вылетании за рамки игрок перемещается в соотвествующий сектор.

Космос

Большую часть я уже изложил, но все же остались некоторые вещи. В каждом из секторов космоса есть по 4 планеты. Когда игрок нажимает на клавишу E, если он находится на расстоянии радиуса от этой планеты, то игрок перемещается на планету.

Враги

ИИ врагов очень тупой — если в радиусе их видимости есть игрок, то они просто стремятся врезаться в него, причем существует небольшая погрешность, по этому их траектория достаточно кривая. Если же в радиусе их видимости игрока нет, то они направляются к своему спаунеру.

Спаунер

В каждом секторе космоса присутствует 1 спаунер. Спаунеры могут быть разных размеров. Размер влияет на дальность видимости игрока. Если игрок находится в зоне их видимости, то спаунер создает врагов каждые 5 секунд, но количество врагов не может превышать 10.

Заключение

Потратив около недели я создал игру, которая не использует никаких .png либо .jpg файлов.

Ссылка на проект на GitHub ^[6]

Для тех, кому лень качать проект и запускать игру, короткий видеоролик по геймплею игры:

Автор: SampleCoder

Источник ^[7]