Решение СЛАУ с матрицей общего вида

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными:

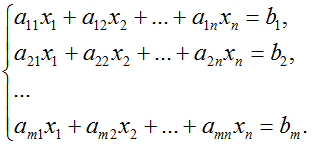
Матрица системы может быть не только квадратной невырожденной, но и квадратной вырожденной или прямоугольной.
Требуется найти все решения данной системы либо определить, что она несовместна (не имеет решений).

Рассмотрим метод Гаусса решения СЛАУ.

Алгоритм решения СЛАУ

Вначале система при помощи элементарных преобразований приводится к ступенчатому виду:

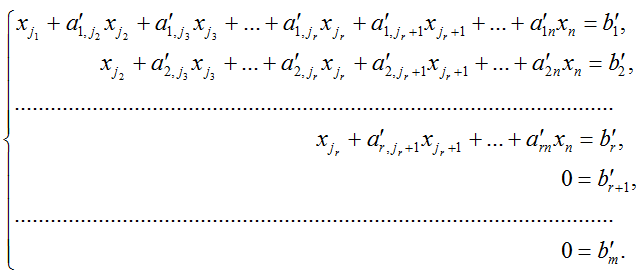
Процесс преобразования системы к ступенчатому виду называется прямым ходом метода Гаусса.
Переменные 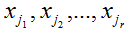называются главными переменными, все остальные переменные называются свободными.
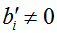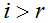Если хотя бы одно число , где , то система несовместна.

Пусть 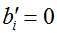для всех 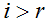. Рассмотрим обратный ход метода Гаусса.
Перенесем свободные переменные в правые части уравнений. Получим

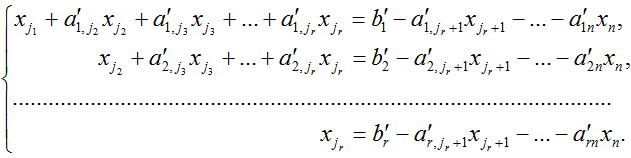
Придадим свободным переменным произвольные значения, а значения главных переменных найдем по формуле

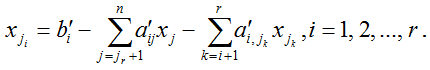
Рассмотрим прямой ход метода Гаусса с выбором главного элемента по столбцу.
Сначала находим в 1-м столбце максимальный по модулю элемент (главный элемент). Если все элементы 1-го столбца равны 0, то переменная x₁ уже исключена, переходим к исключению переменной x₂. Если же не все элементы 1-го столбца равны 0, то меняем местами 1-ю строку и строку, в которой находится главный элемент, а затем исключаем переменную x₁ из 2-го, 3-го, …, m-го уравнений, домножая 1-е уравнение на коэффициенты a_i,1 и вычитая его из всех остальных уравнений.
После исключения переменной x₁ аналогичным образом исключаем переменные x₂, x₃ и т.д.
Разработан модуль для решения СЛАУ методом Гаусса в случае, когда матрица системы может быть квадратной вырожденной или прямоугольной.

Программная реализация

Основная функция модуля — Gauss, которая объявлена следующим образом:

std::vector<std::vector<double> > Gauss(
std::vector<std::vector<double> > a,
std::vector<double> b);

Функция принимает на вход матрицу системы a и вектор правых частей уравнений b. Функция возвращает вектор значений переменных, каждый элемент этого вектора, в свою очередь, является вектором, содержащим коэффициенты при свободных переменных и число, которое прибавляется к линейной комбинации свободных переменных. Если система несовместна, то функция возвращает пустой вектор.
Вектор, содержащий значение переменной, устроен так: нулевой элемент вектора содержит число, которое прибавляется к линейной комбинации свободных переменных, а i-й элемент (i > 1) содержит коэффициент при i-й свободной переменной.

Прямой ход метода Гаусса реализован следующим образом. Переменная i содержит номер текущего рассматриваемого уравнения, а переменная j содержит номер текущей переменной, которую нужно исключить (предполагается, что из уравнений с номерами 1, 2, …, i–1 уже исключены переменные с номерами 1, 2, …, j–1). В процессе прямого хода метода Гаусса вычисляется вектор jj, содержащий номера главных переменных. Также вычисляется переменная r, содержащая число главных переменных.

/* Прямой ход метода Гаусса */

std::vector<int> jj;
int j = 0;
int r = 0;
for (int i = 0; i < m; ++i) {
	double max_abs;
	int k_max;
	while (j <= n-1) {
		//находим максимальный по модулю элемент
		max_abs = 0;
		k_max = i;
		for (int k = i; k < m; ++k) {
			if (fabs(a[k][j]) > max_abs) {
				max_abs = fabs(a[k][j]);
				k_max = k;
			}
		}
		if (!equal(max_abs, 0))
			break;
		++j;
	}
	if (j > n-1)
		break;
	++r;
	jj.push_back(j);
	if (k_max != i) {
		//поменять местами i-ю строчку с k_max-й
		for (int l = j; l < n; ++l)
			swap_double(a[i][l], a[k_max][l]);
		swap_double(b[i], b[k_max]);
	}
	//делим i-е уравнение на a[i][j]
	for (int l = j+1; l < n; ++l) {
		a[i][l] /= a[i][j];
	}
	b[i] /= a[i][j];
	a[i][j] = 1;
	//путём элементарных преобразований обнулить
//элементы a[i+1][j], a[i+2][j], ..., a[m-1][j]
	for (int k = i+1; k < m; ++k) {
		//умножаем i-е уравнение на a[k][j]
//и вычитаем из k-го уравнения
		for (int l = j+1; l < n; ++l)
			a[k][l] -= a[i][l]*a[k][j];
		b[k] -= b[i]*a[k][j];
		a[k][j] = 0;
	}
	++j;
}

Далее система проверяется на совместность.

/* Проверка системы на совместность */

bool flag = true;
for (int i = r; i < m; ++i) {
	if (!equal(b[i], 0)) {
		flag = false;
		break;
	}
}
if (!flag) {
	//система несовместна
	return ans;
}

После этого определяется, какие переменные будут свободными, и свободным переменным присваивается произвольное значение.

/* Определение свободных переменных */

int free_vars_count = n-r;
ans.resize(n);
for (int j = 0; j < n; ++j)
	ans[j].resize(free_vars_count + 1);
if (r == 0) {
	for (int j = 0; j < n; ++j)
		ans[j][j+1] = 1;
}
else {
	int c = 0;
	for (int j = 0; j < jj[0]; ++j) {
		++c;
		ans[j][c] = 1;
	}
	for (int i = 0; i < r-1; ++i) {
		for (int j = jj[i]+1; j < jj[i+1]; ++j) {
			++c;
			ans[j][c] = 1;
		}
	}
	for (int j = jj[r-1]+1; j < n; ++j) {
		++c;
		ans[j][c] = 1;
	}
}

Наконец, выполняется обратный ход метода Гаусса, в ходе которого вычисляются значения главных переменных.

/* Обратный ход метода Гаусса */

for (int i = r-1; i >= 0; --i) {
	ans[jj[i]][0] = b[i];
	for (j = jj[i]+1; j < n; ++j)
		ans[jj[i]] = add(ans[jj[i]], mult(ans[j], -a[i][j]));
}

Вспомогательные функции:

	const double EPS = 1e-12;

	bool equal(double a, double b)
	{
		return fabs(b-a) <= EPS;
	}

	void swap_double(double &a, double &b)
	{
		double tmp = a;
		a = b;
		b = tmp;
	}

	std::vector<double> add(std::vector<double> a, std::vector<double> b)
	{
		std::vector<double> c;
		c.resize(a.size());
		for (int i = 0; i < c.size(); ++i)
			c[i] = a[i] + b[i];
		return c;
	}

	std::vector<double> mult(std::vector<double> a, double k)
	{
		std::vector<double> c;
		c.resize(a.size());
		for (int i = 0; i < c.size(); ++i)
			c[i] = a[i]*k;
		return c;
	}

Ссылки:

1. Метод Гаусса — Википедия. URL: ru.wikipedia.org/wiki/Метод_Гаусса ^[1]
2. Метод Гаусса: описание алгоритма решения системы линейных уравнений, примеры, решения. www.cleverstudents.ru ^[2]. URL: www.cleverstudents.ru/solving_systems_Gauss_method.html ^[3]
3. Метод Гаусса для решения систем линейных уравнений. Математический портал. URL: mathportal.net/index.php/linejnaya-algebra/metod-gaussa-metod-zhordana-gaussa?showall=&limitstart= ^[4]
4. Методы исключения Гаусса. MachineLearning. URL: www.machinelearning.ru/wiki/index.php?title=Методы_исключения_Гаусса ^[5]

Автор: grenkin

Источник ^[6]