Стохастический язык программирования на основе алгоритмов Маркова

MarkovJunior — это вероятностный язык программирования, в котором программы являются сочетаниями правил перезаписи, а инференс выполняется при помощи распространения ограничений. MarkovJunior назван в честь математика Андрея Андреевича Маркова ^[1], придумавшего и исследовавшего то, что сейчас называется алгоритмами Маркова ^[2].

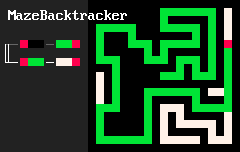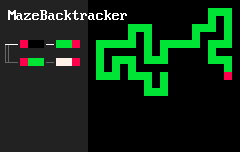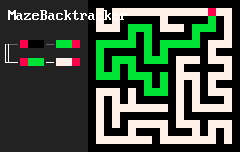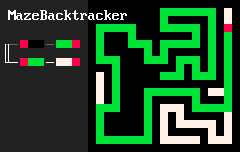
В своей базовой форме программа на MarkovJunior — это упорядоченный список правил перезаписи. Например, показанная ниже анимация MazeBacktracker ^[3] — это список из двух правил перезаписи:

1. RBB=GGR, или «заменить красный-чёрный-чёрный на зелёный-зелёный-красный».
2. RGG=WWR, или «заменить красный-зелёный-зелёный на белый-белый красный».

На каждом этапе исполнения интерпретатор MJ находит в списке первое правило, которое соответствует элементам в сетке, находит все совпадения для этого правила и применяет его к случайному совпадению. В примере maze backtracker ^[4] (алгоритма поиска с возвратом) интерпретатор сначала применяет множество правил RBB=GGR. Но в конце концов зелёное избегающее себя блуждание заходит в тупик. Так как теперь у первого правила нет совпадений, интерпретатор применяет второе правило RGG=WWR, пока блуждание не выйдет из тупика. Затем он снова может применить первое правило, и так далее. Интерпретатор останавливается, когда не остаётся совпадений ни для одного из правил.

Вероятностный инференс в MarkovJunior позволяет накладывать ограничения на будущее состояние и генерировать только те прогоны, которые приводят к будущему с ограничениями. Например, инференс в правилах Sokoban {RWB=BRW RB=BR} заставляет группу агентов (красных) выстраивать ящики (белые) в указанные фигуры.

На основе этих идей мы создали множество вероятностных генераторов ^[5] подземелий, архитектуры, головоломок и интересных симуляций.

Дополнительные материалы:

1. обзор Xml-синтаксиса ^[6].
2. Скриншоты высокого разрешения и дополнительные сиды: ModernHouse ^[7], SeaVilla ^[8], Apartemazements ^[9], CarmaTower ^[10], Escheresque ^[11], PillarsOfEternity ^[12], Surface ^[13], Knots ^[14].
3. Неофициальные технические заметки ^[15] Дэна Оглса и документация кода ^[16] Эндрю Кэя.

Алгоритмы Маркова

Алгоритм Маркова для алфавита A — это упорядоченный список правил. Каждое правило — это строка вида x=y, где x и y — слова алфавита A, а некоторые правила могут быть помечены как правила останова. Применение алгоритма Маркова к слову w выполняется следующим образом:

1. Находим первое правило x=y, где x является подстрокой w. Если таких правил нет, выполняем останов.
2. Заменяем самый левый x в w на y.
3. Если найденное правило является правилом останова, выполняем останов. В противном случае переходим к шагу 1.

Например, рассмотрим следующий алгоритм Маркова для алфавита {0, 1, x} (ε — это пустое слово):

1=0x
x0=0xx
0=ε

Если мы применим его к строке 110, то получим следующую последовательность строк:

110 -> 0x10 -> 0x0x0 -> 00xxx0 -> 00xx0xx -> 00x0xxxx -> 000xxxxxx -> 00xxxxxx -> 0xxxxxx -> xxxxxx

В целом, этот алгоритм преобразует двоичное описание числа в его унарное описание.

Студент Маркова Вилнис Детловс ^[17] доказал ^[18], что для любой машины Тьюринга существует алгоритм Маркова, вычисляющий ту же функцию. Для сравнения: грамматики — это неупорядоченные множества правил перезаписи, а L-системы — это правила перезаписи, применяемые параллельно. Более интересные примеры алгоритмов Маркова можно найти в книге Маркова ^[19]; пример наибольшего общего делителя приведён в комментариях к оригиналу поста ^[20], а пример умножения ^[21] — в Википедии.

Как обобщить алгоритмы Маркова до многомерных операций? Во-первых, при нескольких измерениях не существует естественных способов вставки строки в другую строку, поэтому левые и правые части правил перезаписи должны иметь одинаковый размер. Во-вторых, отсутствуют естественные способы выбрать самое левое совпадение. Решить эту проблему можно следующими способами:

• Выбираем случайное совпадение. Именно так поступают узлы (exists) языка MarkovJunior.
• Выбираем все совпадения. Однако у этого варианта разные совпадения могут пересекаться и иметь конфликты. Возможные решения:
  • Жадный выбор максимального подмножества неконфликтующих совпадений. Именно это делают узлы {forall} языка MarkovJunior.
  • Учёт всех совпадений в суперпозиции. То есть вместо отдельных значений сохраняем в каждой ячейке сетки волны — булевы векторы, сообщающие, какие пространственно-временные паттерны запрещены, а какие нет. И именно так выполняет инференс MarkovJunior.

Мы теряем полноту по Тьюрингу, поскольку наша новая процедура не детерминирована, но практика показывает, что такая формулировка всё равно описывает огромный диапазон интересных случайных процессов.

Правила перезаписи

Наверно, самая простая программа на MarkovJunior — это (B=W). Она содержит всего одно правило B=W. На каждом шаге эта программа преобразует случайный чёрный квадрат в белый.

(B=W)

(WB=WW)

(WBB=WAW)

(WBB=WAW)

Более интересна модель Growth ^[22] (WB=WW). На каждом шаге она заменяет чёрно-белую пару соседних клеток BW бело-белой парой WW. Иными словами, на каждом шаге она выбирает случайную чёрную ячейку, соседнюю с какой-то белой ячейкой, и раскрашивает её в белый цвет. Эта модель практически идентична модели роста Идена ^[23]: на каждом шаге обе модели выбирают в одном множестве чёрных ячеек. Они различаются только распределением вероятностей: равномерное распределение по чёрным ячейкам, соседним с белыми, отличается от равномерного распределения по парам соседних чёрных и белых ячеек.

Модель (WBB=WAW) одной строкой кода генерирует лабиринт! Сравните её с реализацией ^[24] на традиционном языке программирования. Любую модель MarkovJunior можно без изменений выполнять в любом количестве измерений. На последнем из показанных выше изображений показан конечный результат MazeGrowth ^[25] в 3D, отрендеренный в MagicaVoxel ^[26]. По умолчанию мы используем палитру PICO-8 ^[27]:

Модель (RBB=WWR) — это избегающее себя случайное блуждание ^[28]. Стоит отметить, что избегающие себя блуждания в 3D в среднем занимают больше шагов, чем в 2D. В целом, сравнение поведений схожих случайных процессов в разных измерениях — потрясающая тема. В классическом результате ^[29] Джорджа Полиа говорится, что случайное блуждание в 2D возвращается к своей исходной позиции с вероятностью единица, но в 3D это уже не так.

(RBB=WWR)

LoopErasedWalk

(RB=WR RW=WR)

В один rulenode (узел правил) можно поместить множество разных правил. Например, (RBB=WWR RBW=GWP PWG=PBU UWW=BBU UWP=BBR) — это случайное блуждание с удалёнными петлями ^[30]. Модель Trail (RB=WR RW=WR) генерирует красивые соединённые пещеры ^[31].

Модель (RBB=WWR R*W=W*R) известна как алгоритм генерации лабиринтов Олдоса-Бродера ^[32]. Символ подстановки * во вводе означает, что в квадрате может быть любой цвет. Символ подстановки в выводе означает, что после применения правила цвет не меняется. В среднем алгоритм Олдоса-Бродера требует гораздо больше шагов для генерации лабиринта, чем, например, MazeGrowth, но обладает удобным свойством, которого нет у MazeGrowth: вероятность генерации каждого из лабиринтов одинакова. Иными словами, MazeTrail — это алгоритм генерации лабиринтов без перекоса, то есть он сэмплирует лабиринты (или связные деревья) с равномерным распределением. Ещё более эффективный алгоритм генерации лабиринтов без перекосов — алгоритм Уилсона ^[33]. Сравните его реализацию ^[34] на MarkovJunior ^[35] с реализацией ^[36] на традиционном языке!

Комбинирование узлов правил

Можно поместить множество узлов правил в узел последовательности для выполнения один за другим. В модели River ^[37] мы сначала создаём стохастическую диаграмму Вороного ^[38] с двумя источниками и используем границу между образованными областями как основание для реки. Затем мы создаём ещё пару сидов Вороного, чтобы вырастить леса и параллельно растить траву от реки. В результате этого мы получаем случайные долины рек!

В Apartemazements ^[39] мы начинаем с узла WFC, а затем выполняем конструктивную постобработку при помощи узлов правил:

1. Подготавливаем ограничения: помечаем нижние ячейки отдельным цветом низа, помечаем оставшиеся ячейки границ (бока и верх) отдельным цветом границ. Ячейки границ должны отображаться в Empty, нижние ячейки должны отображаться во все тайлы, кроме Down.
2. Выполняем тайлсет Paths ^[40] WFC для генерации циклов замкнутых лестниц.
3. Рандомизируем источники освещения.
4. Сбрасываем столбцы с углов плоских тайлов.
5. Убираем двойные столбцы, столбцы, которые касаются земли и столбцы, которые касаются лестниц, за исключением столбцов, растущих из углов тайлов Turn.
6. Выращиваем окна между соседними столбцами.
7. Объединяем окна в прямоугольники большего размера. Делаем это в несколько шагов:
   1. Выявляем неровные паттерны окон, когда углы окон касаются средних точек окон.
   2. Помечаем эти паттерны и распространяем пометки на полные длины боков окон.
   3. Объединяем непомеченные пары боков окон.

8. Превращаем оставшиеся окна размером 1x1 в стены.

Более интересный способ объединения узлов заключается в объединении их в узел Маркова. Узлы Маркова существенно расширяют наши возможности, потому что они позволяют возвращаться к предыдущим узлам. Когда узел Маркова активен, интерпретатор находит его первый дочерний узел, имеющий совпадение, и применяет его. На следующем шаге он снова находит следующий совпадающий узел в списке, и так далее. Простейший пример использования узлов Маркова — это MazeBacktracker ^[3], объяснённый в одном из предыдущих разделов.

Один из моих примеров, мотивировавших меня на разработку MarkovJunior — это алгоритм генерации подземелий Боба Нистрома ^[41]. Он имеет следующий вид:

1. Рисуем сетку {PBB=**P}.
2. Создаём серию комнат (room.png).
3. Генерируем лабиринт в оставшейся части сетки. Можно использовать любой алгоритм генерации лабиринтов, но предпочтителен MazeBacktracker ^[3], потому что он создаёт меньше точек ветвления.
4. Делаем получившуюся конфигурацию комнат и коридоров соединённой. Это изящным способом можно сделать при помощи узла Маркова ({GWW=**G}(GBW=*WG)).
5. Создаём дополнительные соединения (GBG=*W* #5), чтобы получившееся подземелье имело петли. Подземелья без петель довольно скучны, потому что игроку приходится возвращаться через уже исследованные зоны.
6. Удаляем тупики {BBB/BWB=BBB/BBB}.

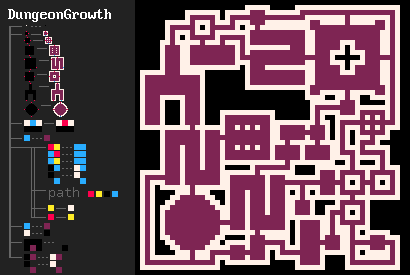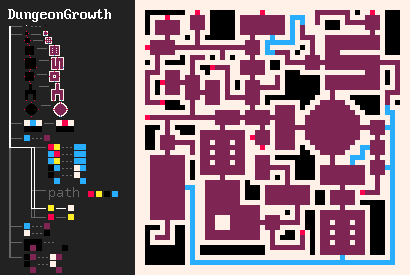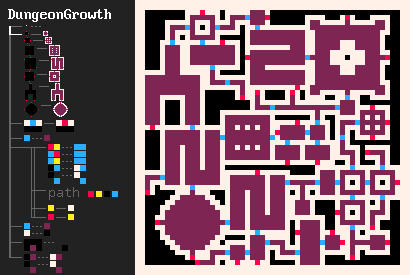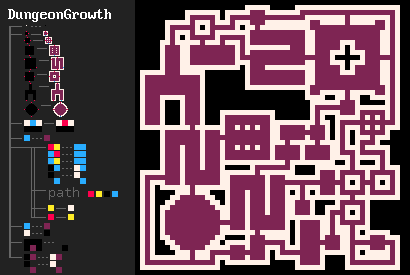
Как в Рефале, узлы Маркова могут быть вложенными: зайдя в дочерний узел, мы игнорируем внешние узлы, пока не завершится дочерняя ветвь.

Инференс

Вероятностный инференс в MarkovJunior позволяет накладывать ограничения на будущее состояние и генерировать только те прогоны, которые ведут к будущему с ограничениями. Иными словами, инференс соединяет два заданных состояния (или частично наблюдаемых состояния) цепочкой правил перезаписи.

Простейший пример использования инференса — это соединение двух точек путём. В модели блуждания с избеганием себя (RBB=WWR) мы можем наблюдать, как квадрат на сетке становится красным (R). Тогда интерпретатор генерирует только те блуждания, которые ведут к наблюдаемому квадрату. Мы можем настроить интерпретатор так, чтобы он стремился к цели более или менее строго, меняя параметр температуры. По умолчанию температура установлена на ноль.

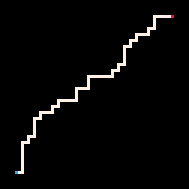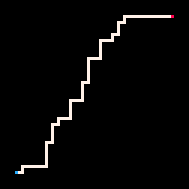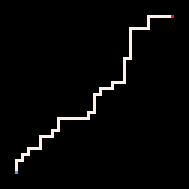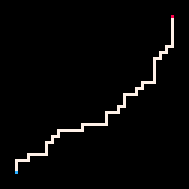
Самая низкая температура

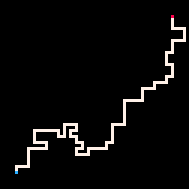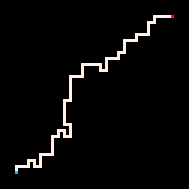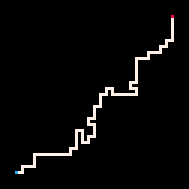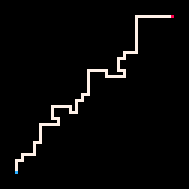
Холодная

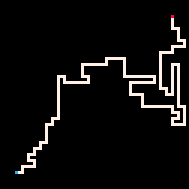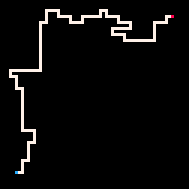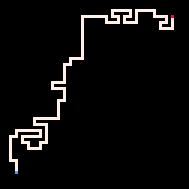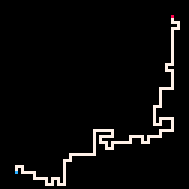
Горячая

Максимально высокая

Также мы можем наблюдать за тем, как все нечётные квадраты сетки становятся белыми или красными. Тогда интерпретатор генерирует блуждания с избеганием себя, покрывающие всю сетку.

Мы можем задействовать инференс для любых правил перезаписи. Например, инференс для правил рисования лестниц ^[42] соединяет две точки путём-лестницей. Инференс для правила R**/**B=B**/**R генерирует пути, которыми может двигаться шахматный конь. Инференс модели CrossCountry ^[43] соединяет две точки путём, учитывающим стоимость перемещения по разным типам рельефа. Инференс для набора правил Sokoban {RB=BR RWB=BRW} решает головоломки Sokoban или даже головоломки Sokoban с несколькими агентами ^[44]!

Инференс в MarkovJunior выполняется однонаправленным (быстрое) или двунаправленным (медленное, но более мощное) распространением ограничений. Однонаправленное распространение ограничений для правил перезаписи можно эквивалентно описать на основе полей распространения правил, которые обобщают поля Дейкстры для произвольных правил перезаписи. Правила Дейкстры — популярная техника процедурной генерации на сетках (1 ^[45], 2 ^[46], 3 ^[47]). Они, в свою очередь, обобщают поля расстояний ^[48], используемые в компьютерной графике.

Если распространение ограничений завершается успешно, это необязательно значит, что целевое состояние достижимо. Но если распространение завершается неудачно, то мы точно знаем, что цель недостижима. Это позволяет отлавливать в Sokoban состояния, когда ящик толкают не к той стене, или когда блуждание с целью заполнения сетки разделяет сетку на две разделённые части. В дополнение к булевой эвристике стоит отслеживать минимальное количество шагов, необходимое для успешного завершения распространения ограничений. Эвристика с целочисленными значениями приемлема ^[49], и мы используем её в поиске A* для сэмплирования путей, созданных из правил перезаписи между двумя заданными состояниями.

Нерешённые проблемы

1. Синтез программ для процедурной генерации. Доклад Уильяма Чира «Level Design in Impossible Geometry» ^[50] посвящён не совсем процедурной генерации, однако оказался очень характерным для процедурной генерации контента. Уильям сравнивает свои начальный и более поздний подходы к дизайну уровней. В начале он создавал хаотические уровни, а позже — более структурированные, более осмысленные уровни, основанные на одной центральной идее. Такие уровни не были проще, они лишь лучше запоминались и воспринимались игроками.
   

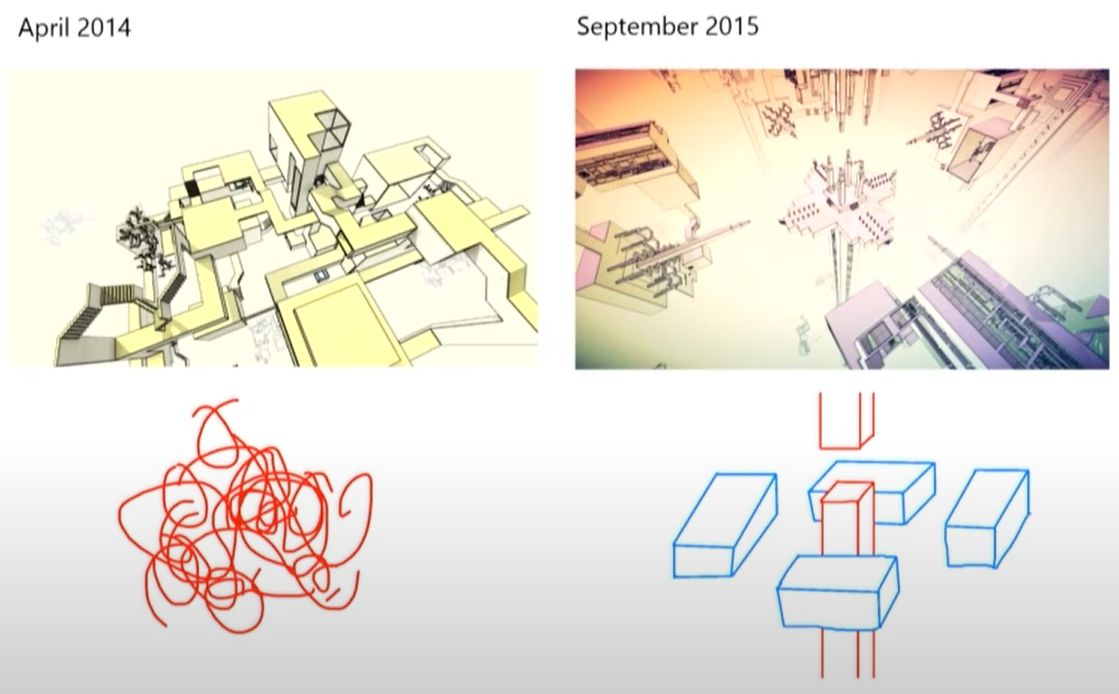
   На мой взгляд, левый уровень выглядит так, как будто генерировался процедурно! Он очень похож по ощущениям на мои процедурные воксельные головоломки ^[51]. Можем ли мы писать генераторы, создающие уровни, которые больше похожи на правый? Может показаться, что ИИ готов справиться с такой задачей. Но я возражу, что она очень похожа на классические задачи генетического программирования наподобие задачи газонокосилки Козы ^[52]. Например, возьмём простую задачу процедурной генерации по созданию гамильтоновых путей на сетке ^[53]. Даже для небольших размеров сетки наподобие 29x29 эта задача уже вычислительно затратна. Но действительно ли нам нужно на практике сэмплировать из всех возможных путей? Если мы дадим эту задачу человеку, то он, скорее всего, нарисует спираль или зигзаг, а это гораздо более запоминающиеся и логичные структуры, чем случайный гамильтонов путь, плюс их можно обобщить до любых размеров сетки. Подведём итог: мы можем попросить систему или найти случайный гамильтонов путь, или короткую программу, генерирующую гамильтоновы пути. В первом случае результат будет похож на левый уровень слайда, во втором случае — на правый уровень. Решение задачи синтеза программ создаст более запоминающиеся и логичные генераторы.

2. Синтез моделей из примеров. Похоже, алгоритмы Маркова — идеальная среда для синтеза программ/моделей: никаких переменных, if или while, узлы можно легко перемещать без нарушения корректности, модели легко делать различающимися. Случайные программы на Random MarkovJunior часто любопытны и могут создавать приятные человеку результаты и поведения.
   1. Можно ли синтезировать модель MarkovJunior из результата или множества результатов?
   2. Можно ли определить (или присвоить вероятности), сгенерирован ли лабиринт MazeGrowth ^[25] или MazeBacktracker ^[3]?
   3. Решить Abstraction and Reasoning Challenge ^[54] инференсом моделей MarkovJunior. Примыкающая задача: использовать наблюдения из ARC с целью создания улучшенного DSL для процедурной генерации на сетке.
3. Произвольные алгоритмы, выполняемые в волновом пространстве. Объединить преимущества конструктивной процедурной генерации и генерации на основании ограничений. Связанная задача: произвольные алгоритмы (правила перезаписи MarkovJunior) с произвольными функциями энергии, например, энергии Изинга или энергии ConvChain.
4. Обобщение записи паттерна.
5. Исследование подобных MarkovJunior процессов на других (возможно, неравномерных) сетках или произвольных графах.
6. Эксперименты с интерактивными расширениями алгоритмов Маркова. Можно превратить любую модель MarkovJunior в игру, присвоив нажатиям клавиш правила или узлы перезаписи.
7. Расширение возможностей процедурной генерации на сетках. ModernHouse ^[55] пока не достиг структурной вариативности создаваемых людьми домов, например, домов в Sims 2 ^[56]. Нужно применять более тонкие ограничения.

Комментарии

По сравнению с машинами Тьюринга и лямбда-исчислением, алгоритмы Маркова, вероятно, простейший и кратчайший способ формулирования строгого определения того, что же такое алгоритм.

Упражнение: доказать, что следующий алгоритм Маркова находит наибольший общий делитель двух чисел, записанных в унарном представлении. Например, если мы применим его к 111111*1111111111, то получим 11.

1a=a1
1*1=a*
1*=*b
b=1
a=c
c=1
*=ε (останов)

Быстрое сопоставление паттернов. Сэмплы интерпретатора MarkovJunior совпадают равномерно, но на каждом шаге он не сканирует всю сетку. Чтобы сохранить высокую скорость сопоставления паттернов, интерпретатор запоминает ранее найденные совпадения и ищет только вокруг изменившихся участков. Когда узел правил встречается в первый раз, интерпретатор MarkovJunior использует многомерную версию алгоритма Бойера-Мура ^[57].
Стохастическая релаксация. Узлы Маркова имеют очень удобные описания как границы дифференцируемых узлов. Рассмотрим неупорядоченное множество правил перезаписи, где каждому правилу r присвоен вес w(r). На каждом шаге интерпретатор находит все совпадения для всех правил и выбирает случайное совпадение согласно распределению Больцмана p(r) ~ exp(-w(r)/t). Находясь на границе замерзания t->0, мы получаем узел Маркова, упорядоченный по весам. В этой конструкции удобно то, что для любой t>0 и для типичной функции отсчёта среднее значение отсчёта в многократных прогонах будет непрерывной (и гладкой для практических применений) функцией весов. Это значит, что можно найти оптимальные веса при помощи градиентного спуска, а затем заморозить систему, чтобы получить готовую дискретную программу.

Прочитайте это эссе ^[58] Бориса Кушнера ^[59] об А.А. Маркове и его работах по конструктивной математике.

Использованные труды

Главный использованный труд:

1. Андрей А. Марков, The Theory of Algorithms ^[60], 1951 год. Марков использовал эти идеи ещё в 1947 году для доказательства алгоритмической неразрешимости задачи тождества слов в полугруппах. См. также более позднюю книгу ^[61] с более подробным разбором. Я был бы благодарен за ссылки на английские переводы в открытом доступе.
2. Guilherme S. Tows, Imagegram ^[62], 2009 год. Узлы forall для MarkovJunior взяты из Imagegram.
3. Валентин Турчин, REFAL language ^[63], 1968 год. Идея вложенных узлов Маркова взята из Рефала.
4. Brian Walker et al., The incredible power of Dijkstra maps ^[45], 2010 год. Обсуждение в сообществе разработчиков roguelike, содержащее множество техник применения карт/полей расстояний Дейкстры для процедурной генерации и искусственного интеллекта NPC. Другие статьи: 1 ^[46], 2 ^[47]. Мы обобщаем карты Дейкстры до произвольных правил перезаписи.
5. Pavlos S. Efraimidis, Paul Spirakis, Weighted Random Sampling ^[64], 2005 год.
6. Работы, использованные для произвольных узлов: Model Synthesis ^[65], Wave Function Collapse Algorithm ^[66], ConvChain Algorithm ^[67].
7. Классические алгоритмы: распространение ограничений ^[68], алгоритмы решения ограничений ^[69], обход графов ^[70], поиск A* ^[71].

Связанные работы:

1. Daniel Ritchie, Probabilistic Programming for Procedural Modeling and Design ^[72], 2016 год.
2. Lingfeng Yang, From Execution Traces to Specialized Inference ^[73], 2015 год.

Источники примеров:

1. BasicKeys ^[74] и Keys ^[75] — адаптации графовых грамматик, сформулированных Йорисом Дормансом в Engineering Emergence: Applied Theory for Game Design ^[76], 2012 год. Они, в свою очередь, являются дальнейшим развитием работы Дэвида Адамса Automatic Generation of Dungeons for Computer Games ^[77], 2002 год. Я использовал вариацию этих моделей для генерации головоломок «ключ-замок-мост» в SeaVilla ^[78].
2. CarmaTower ^[79] — процедурализация воксельной сцены ^[80] Антуана Лендреви.
3. Модель NystromDungeon ^[81] — это порт генератора подземелий Боба Нистрома ^[41] для MarkovJunior.
4. Алгоритм HamiltonianPath ^[82] адаптирован из этой ^[83] статьи. Сравните его с реализацией ^[84] на традиционном языке.
5. Формы комнат в DungeonGrowth ^[85] взяты из поста на r/proceduralgeneration ^[86]. Обратите внимание, что интерпретатор MarkovJunior автоматически выполняет описанные в посте оптимизации.
6. Модель Wilson ^[34] — это формулировка в правилах перезаписи алгоритма Уилсона ^[87]. Сравните её с реализацией ^[36] на традиционном языке.
7. Модель MazeGrowth ^[25] также известна как генерация лабиринтов при помощи случайного обхода (maze generation via random traversal). Сравните её с реализацией ^[24] на традиционном языке.
8. Growth ^[22] тесно связана с моделью роста Идена ^[23].
9. BernoulliPercolation ^[88] — это хорошо изученная модель в теории перколяции ^[89].
10. NestedGrowth ^[90] взята из Imagegram ^[62].
11. SmoothTrail ^[91] адаптирована из твита 128_mhz ^[92].
12. SokobanLevel1 ^[93], похоже, является первым уровнем из головоломки Sokoban Хироюки Имабаяси. SokobanLevel2 ^[94] — это уровень 452 ^[95] из набора Ionic Catalysts XI.
13. RainbowGrowth ^[96] была предложена ^[97] пользователем mure ^[98].
14. MultiHeadedWalk ^[99], MultiHeadedDungeon ^[100] и MultiHeadedWalkDungeon ^[101] основаны ^[102] на идее Ильи Кудрицкого ^[103].
15. Модель Island ^[104] создана Гийомом Фьетом ^[105].
16. Модели LostCity ^[106], Forest ^[107] и Texture ^[108] основаны на модели Эндрю Кэя ^[109].

Воксельные сцены отрендерены в MagicaVoxel ^[26], разработанной ephtracy ^[110]. Особая благодарность Брайану Баклью ^[111] за демонстрацию мощи полей Дейкстры на примере генерации уровней roguelike и Кевину Шапелье ^[112] за множество хороших подсказок. В GUI использован шрифт Tamzen ^[113].

Как выполнять сборку

Интерпретатор MarkovJunior — это консольное приложение, зависящее только от стандартной библиотеки. Установите .NET Core ^[114] для Windows, Linux или macOS и выполните следующую команду:

dotnet run --configuration Release MarkovJunior.csproj

Также можно скачать и запустить последний релиз ^[115] для Windows.

Сгенерированные результаты помещаются в папку output. Для изменения параметров моделей отредактируйте models.xml. Файлы .vox открываются при помощи MagicaVoxel ^[26].

Важные порты, форки и спиноффы

• Yuu создал версию MarkovJunior на TypeScript ^[116], которая выполняется в вебе ^[117], расширяет язык и добавляет возможность привязки узлов к нажатиям клавиш.
• Aseaday портирует ^[118] MarkovJunior на JavaScript.
• Эндрю Кэй добавил к исходному коду на C# документацию по XML ^[16].
• Дэн Оглс ^[119] написал технические заметки ^[15] по MarkovJunior с упором на поля и инференс.
• Эндрю Кэй спроектировал MJr ^[120] — компилируемый язык, основанный на перезаписи паттернов.