Я написал алгоритм вычисления дат, который на 30–40% быстрее остальных

В этой статье я представлю мой завершённый очень быстрый алгоритм преобразования дат. Он обеспечивает существенный прирост скорости, по величине сравнимый с приростом, достигнутым предыдущим самым быстрым алгоритмом (Neri-Schneider 2021) относительно его предшественника (C++ Boost). Полная реализация алгоритма на C++ выпущена как свободное и бесплатное ПО (лицензия BSL-1.0).

Алгоритм генерирует точные результаты за период ±1,89 триллиона лет, поэтому подходит для обработки полного 64-битного времени UNIX (в секундах).

Весь алгоритм был переписан сверху вниз с различными микрооптимизациями, но три его основные принципа сохранились:

• Годы вычисляются в обратном направлении, что позволяет избавиться от различных промежуточных этапов.

• Этап вычисления дня года пропущен; вместо него используется методика побитового сдвига остатка от деления года, что позволяет избавиться от деления.

• Применена методика Julian Map из моей предыдущей статьи, ускоряющая вычисления годов 100/400 и избавляющая ещё от двух аппаратных операций умножения.

Быстрые алгоритмы вычисления даты всегда использовали 7 или более затратных вычислений (умножение, деление или деление с остатком на числа, отличные от степеней двойки), но в этом алгоритме применяются всего 4 умножения. Сразу можно понять, что рост скорости должен быть существенным.

Результаты бенчмарка соответствуют ожиданиям при подсчёте операций вручную:

Сначала я представлю общий алгоритм в псевкоде, потом объясню, почему он считает годы назад, а затем разберу его построчно с объяснением каждого этапа. Далее я освещу оптимизации под платформы (x64 и ARM / Apple Silicon), расскажу подробности диапазона/точности, рассмотрю различные варианты отката к 32-битным архитектурам и, наконец, представлю результаты бенчмарков (которые вы сможете проверить сами).

---

Полный алгоритм

Цветами отмечено следующее:

• Красный: затратные операции (например, четыре умножения)

• Зелёный: операции, которые на процессорах x64 «бесплатны»

• Сиреневые комментарии: самые примечательные новые концепции

Пусть   days = количество дней после эпохи, где «1970-01-01» — это ноль. Тогда:

const ERAS = 4726498270 // Для 32 бит использовать 14704
const D_SHIFT = 146097 * ERAS - 719469
const Y_SHIFT = 400 * ERAS - 1
const C1 = 505054698555331 // floor(2^64*4/146097)
const C2 = 50504432782230121 // ceil(2^64*4/1461)
const C3 = 8619973866219416 // floor(2^64/2140)

/* Учитываем правило високосных лет 100/400. */
rev = D_SHIFT - days // Обратный подсчёт дней
cen = (rev * C1) >> 64 // Делим на 36524.25
jul = rev + cen - cen / 4 // Julian map

/* Определяем год и часть года. */
num = jul * C2 // Делим на 365.25
yrs = Y_SHIFT - (num >> 64) // Прямой порядок года
low = num % (1 << 64) // Младшие 64 бита
ypt = (782432 * low) >> 64 // Часть года (в обратном порядке)
bump = ypt < 126464 // Январь или февраль
shift = bump ? 191360 : 977792 // Смещение месяца

/* Побитовый сдвиг остатка деления года для високосных лет. */
/* Обращаем, чтобы получить прямой порядок. */
N = (yrs % 4) * 512 + shift - ypt
D = ((N % 65536) * C3) >> 64 // Делим на 2140

day = D + 1
month = N / 65536
year = yrs + bump

Примечание:

• Это версия алгоритма, оптимизированная под x64. Раздел про оптимизации под ARM см. ниже.

---

Зачем считать в обратном порядке

Неудивительно, что большинство (если не все) быстрые алгоритмы преобразования дат считали годы в прямом направлении, это интуитивно понятный выбор.

При этом получались выражения в формате (foo * 4 + 3) / N. Это один из самых распространённых паттернов в быстрых алгоритмах. Ниже показан пример из C++ Boost (полная версия):

century = (days * 4 + 3) / 146097       // Деление на 36524.25
// ...
year = (dayOfCentury * 4 + 3) / 1461    // Деление на 365.25

Умножение на 4 и деление на 146097 и 1461 понять не так сложно: большие константы — это количество дней, соответственно в 400 годах и в 4 годах. Но что же такое + 3?

Из-за более длинных лет и веков возникает незначительное смещение от эпохи. Проще всего это понять, посмотрев на показанные ниже таблицы. В первой таблице показано распределение високосных лет при счёте с нулевого года:

Так как грегорианский високосный год пропускает обычный високосный год каждые 100 лет, если только год не кратен 400, то мы получаем такой же паттерн для веков:

Если мы сможем найти способ считать даты от эпохи, при котором они обе сразу начинаются с високосного/длинного (вместо смещения на 3), то сможем избавиться от + 3. Более того, мы получим способ объединения foo * 4 / N в одно умножение и побитовый сдвиг. Потенциально это позволит устранить из алгоритма до четырёх тактов CPU (однако конкретный рост скорости будет зависеть от платформы).

Сначала я попробовал сделать это, установив эпоху на год -100 (101 до н.э.), но это решает только половину проблемы: срезы веков обязаны заканчиваться на дате XX00-02-2Y, то есть они должны начинаться непосредственно после февраля в году, кратном 4.

Как вы уже знаете, оказалось, что для полного решения этой проблемы нужно считать в обратную сторону:

Благодаря этому эпоха может начинаться в високосный год, как показано выше, а также начинаться в длинном веке, как показано ниже:

К счастью, переворот временной шкалы никак не сказывается на скорости, потому что во всех алгоритмах работы с датами обычно есть выравнивание эпохи. Достаточно будет просто использовать минус там, где обычно выполняется сложение.

Разобравшись с основной концепцией, можно перейти к подробностям отдельных этапов алгоритма.

---

ПОСТРОЧНОЕ ОБЪЯСНЕНИЕ АЛГОРИТМА

Обратив временную шкалу, можно начинать объяснять алгоритм с самого начала:

Пусть   days = дни с эпохи, где «1970-01-01». Тогда:

Алгоритм — этап 1

const ERAS = 4726498270
const D_SHIFT = 146097 * ERAS - 719469
// ...
rev = D_SHIFT - days            // Обратный счёт дней

Константа D_SHIFT вычисляется во время компиляции:

• 719469 — это количество дней, которое нужно отсчитать назад от эпохи UNIX 1970-01-01 до 0000-02-29 — нашей точки естественного выравнивания. Стоит отметить, что это на один день раньше даты, от которой начинают отсчёт многие другие алгоритмы: 0000-03-01.

• 146097 — это количество дней в 400-летней эре, и мы будем прибавлять большое кратное ей число ERAS, чтобы задать точку обратного отсчёта из далёкого будущего. В таблицах примеров мы ведём обратный отсчёт с 2400, что в этом случае будет означать ERAS = 6.

Конкретное число ERAS = 4726498270 было выбрано для обеспечения максимально возможного диапазона, центрированного относительно эпохи UNIX в 64 битах. При работе с 32 битами применимо значение 14704.

В вычислении rev используется знак минуса для переворота временной шкалы.
 

Алгоритм — этап 2

const C1 = 505054698555331      // floor(2^64*4/146097)
// ...
cen = (rev * C1) >> 64          // Деление на 36524.25

На этом этапе мы выполняем то, что раньше было cen = (days * 4 + 3) / 146097, но всего с одним умножением. Выполнение деления при помощи умножения с последующим побитовым сдвигом (mul-shift) — очень распространённая техника в проектировании низкоуровневых алгоритмов. Если используется реальное деление, то компилятор выведет нечто подобное, но с большим побитовым сдвигом.

Есть две причины писать вручную наш собственный mul-shift

1. Нам нужно целочисленное деление на 36524.25, а это невозможно при обычном целочисленном делении.

2. Мы можем указать побитовый сдвиг ровно на 64, что на 64-битных компьютерах происходит «бесплатно».

Побитовый сдвиг на 64 в данном случае «бесплатен» благодаря тому, как работают 64-битные компьютеры. Так как они не могут хранить в одном регистре число, больше 64 бит, умножение помещает полный 128-битный результат в два соседних регистра. Поэтому побитовый сдвиг на 64 — это просто скомпилированный машинный код, использующий первый из двух регистров, то есть не выполняющий никакой работы.

При обычном делении компилятор использует больший побитовый сдвиг потому, что при астрономически больших значениях эти вычисления перестанут быть корректными. А нам не нужно, чтобы они были корректными всегда, для применения алгоритма достаточно только очень большого диапазона. Компилятор не знает о таких требованиях, поэтому обычно подходит консервативно и выбирает более точный, большой и затратный побитовый сдвиг.
 

Алгоритм — этап 3

jul = rev + cen - cen / 4       // Julian map

Это тоже «новый» этап, не используемый в недавних быстрых алгоритмах вычисления дат.

Здесь мы быстро и эффективно учитываем 100-летние и 400-летние правила високосности. В алгоритмах Boost и Neri-Schneider применяются альтернативные этапы конкретного дня в соответствующем 400-летнем блоке (затратное деление с остатком или вычитание и умножение), а позже конструируют год ещё одним затратным сложением и умножением.

Я писал об этой методике в своей предыдущей статье. Её использовали проектировщики некоторых устаревших алгоритмов дат, но выигрыш в скорости был или недопонят, или нечётко донесён проектировщикам последующих алгоритмов. Подробности я рекомендую изучить в статье по ссылке.
 

Алгоритм — этап 4

const Y_SHIFT = 400 * ERAS - 1
// ...
const C2 = 50504432782230121    // ceil(2^64*4/1461)
// ...
num = jul * C2                  // Деление на 365.25
yrs = Y_SHIFT - (num >> 64)     // Прямой порядок года
low = num % (1 << 64)           // Младшие 64 бита

Здесь мы снова выполняем быстрое деление при помощи единственного умножения; предыдущим алгоритмам здесь нужно было сначала вычислять 4 * jul + 3. На этот раз мы не выполняем сразу побитовый сдвиг на 64, потому что будем использовать и старшую, и младшую части результата. Эта техника впервые появилась в алгоритме Neri‑Schneider.

Старшая 64-битная часть num представляет количество лет, прошедших в обратную сторону с нашей будущей эпохи, поэтому вычтя из неё тщательно подобранную константу, мы получим правильный год. Как и в большинстве других быстрых алгоритмов, этот год позже нужно будет увеличить, если выяснится, что месяцем оказался январь или февраль, поскольку внутренняя логика алгоритма считает началом года 1 марта.

Старшие 64 бита объяснить просто, а младшие 64 биты будут обрабатываться иначе.
 

Алгоритм — этап 5

ypt = (782432 * low) >> 64      // Часть года (в обратном порядке)

Здесь всё будет сильно отличаться. В алгоритме Neri-Schneider младшие биты делятся на константу для вычисления точного day_of_year (0-365). Затем этот day_of_year снова умножается для получения месяца и дня.

На первый взгляд кажется, что деление с последующим умножением можно объединить в одну комбинированную операцию. Однако этап деления обеспечивает важное целочисленное округление, и от этого округления нельзя избавиться, не изменив результат.

В этом алгоритме мы намеренно пропускаем этап day_of_year и объединяем умножение и деление, чтобы получить year-part. Так мы временно теряем влияние округления, что вызывает дрейф значения year-part, равное 1/4 дня на год со сбросом каждые 4 года. Мы допускаем возникновение этой «погрешности» и корректируем её позже при помощи техники побитового сдвига остатка от деления. Пока запомните это, мы вернёмся к этому, когда будем конструировать N в строке 27 (этап 7).

Алгоритм — этап 6

bump = ypt < 126464             // январь или февраль
shift = bump ? 191360 : 977792  // смещение месяца

Мы будем использовать понятие bump, позаимствованное из Neri-Schneider, для обозначения того, что год, начинающийся 1 марта, выполняет переполнение на следующий календарный год, то есть месяцем оказывается январь или февраль. Для вычисления этого в других алгоритмах часто используется day_of_year или month, однако мы не вычисляем day_of_year, и нам понадобится bump для вычисления month. Поэтому мы определим это значение заранее при помощи более запутанного способа. Стоит отметить, что ypt (часть года) по-прежнему указана в обратном направлении, поэтому «последние» месяцы январь и февраль (последние для вычисленного года, начинающегося с 1 марта) — это малые числа, а не более естественные высокие, как можно было бы обычно ожидать.

Далее, shift — это значение, которое будет использоваться в следующей строке для сдвига линейного уравнения на 12 месяцев для достижения подобного переполнения bump на наш год. Стоит отметить, что разность между двумя вариантами «сдвига» равна 786432, то есть 12 × 2¹⁶. Так как в следующем линейном уравнении в качестве знаменателя используется 2¹⁶, так мы обеспечиваем сдвиг на 12 месяцев там, где это требуется, ценой всего одного такта CPU.

В других алгоритмах быстрого вычисления даты часто ближе к концу есть этап вида month = bump ? month - 12 : month, однако на процессорах x64 для его вычисления требуется два такта CPU, потому что M - 12 всегда должно вычисляться до выполнения тернарной проверки.
 

Алгоритм — этап 7

/* Побитовый сдвиг от деления года для високосных лет. */
/* Также выполняется переворот в прямом направлении. */
N = (yrs % 4) * 512 + shift - ypt

Это та самая магия побитового сдвига от деления года, о которой говорилось выше. Значение N будет разбито на две части: старшие 16 бит будут значением month , а младшие 16 бит будут соответствовать day.

Сдвиг мы уже объясняли, но (yrs % 4) * 512 выглядит довольно необычно. Если говорить простыми словами, мы притворяемся, что месяцы длятся 32 дня, это отражает ежегодный сдвиг ровно на 1/4 дня (со сбросом каждые четыре года). Так обнуляется погрешность, о которой мы говорили на этапе 5.

Почему 1/4 дня?
В нашей ложной модели с месяцами из 32 дней 512 единиц соответствует ровно одной четверти дня в 16-битном пространстве. В двоичном виде 512 — это (2¹⁶ / 32) / 4, то есть одна четверть одного ложного дня. Кроме того, значение 512 — это степень двойки, поэтому это компилируется в простой сдвиг влево на 9.

Разумеется, реальные месяцы григорианского календаря не состоят ровно из 32 дней, но они достаточно близки к 32 дням, чтобы это сработало. В допустимом диапазоне сдвига есть достаточно пространства для манёвра, чтобы округление точно соответствовало всем месяцам.

Примечание: поначалу кажется, что эта хитрость только помогает сэкономить минимальное количество тактов, но на самом деле этот этап необходим, чтобы избежать неудобных +3, от которых мы так упорно старались избавиться ранее. Если бы мы продолжали использовать методику из Neri–Schneider со строки 17 и дальше, это смещение снова бы вылезло.

Для этого трюка очень удобно то, что длины месяцев в юлианском и григорианском календарях близки к степени двойки. Возможно, для других календарей, длины месяцев в которых ближе к синодическому лунному месяцу, эту технику нельзя было бы применить. 

Алгоритм — этап 8

const C3 = 8619973866219416     // floor(2^64/2140)
// ...
D = ((N % 65536) * C3) >> 64    // Деление на 2140

Это последний нетривиальный этап, на котором мы берём младшие 16 бит и сопоставляем их с номером дня. Этот номер дня будет значением в интервале 0-30, для которого выполняется инкремент в конце.

Здесь Neri-Schneider использует деление на 2141, однако я выяснил, что значение 2140, похоже, требовалось для реализации техники побитового сдвига остатка от деления года. Мы можем также использовать созданный вручную mul-shift, чтобы побитовый сдвиг оказался «бесплатной» 64-битной вариацией.

Алгоритм — этап 9

day = D + 1
month = N / 65536
year = yrs + bump

Далее мы подчищаем значения так, как это описано выше:

• Выполняем инкремент дня, чтобы значения начинались с единицы

• Берём старшие 16 бит N, получая month

• Выполняем переполнение year, когда месяц оказывается январём или февралём.

Вот и всё. Дата теперь вычисляется самым быстрым способом.

Оптимизации для Arm64 и Apple Silicon

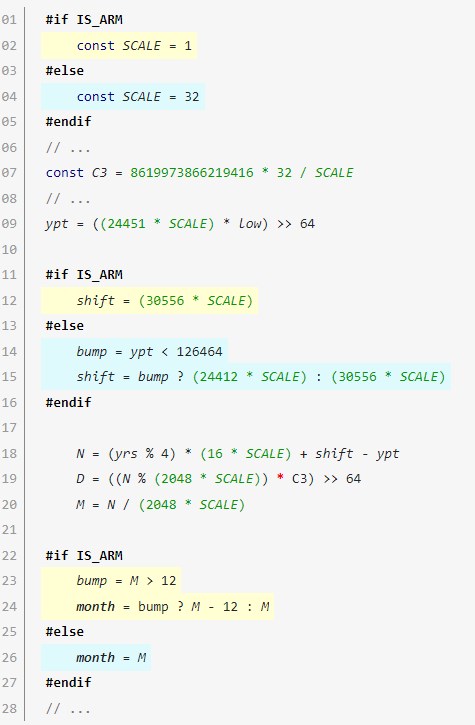
Многие чипы ARM тратят больше времени на загрузку целых чисел больше 16 бит (максимальное значение 65535). В строках 17-25 есть несколько чисел больше этого порогового значения, а именно 782432, 126464, 191360, 977792, 65536.

Их размер таков, потому что они обеспечивают вычисление D при помощи N % 65536; при компиляции этой команды берутся младшие 16-бит N, что на x64 является бесплатной операцией.

Эти константы тщательно подобраны так, чтобы делиться на 32. Можно использовать проверку во время компиляции для деления этих констант на 32, если в качестве целевой платформы выбран ARM (или использовать меньшие значения констант и масштабировать их на 32 для x64). Если сделать это, по размеру они все уместятся в 16 бит, что приведёт к росту производительности на многих чипах ARM. В таком случае изменения требуют и другие константы: если поделить 512 на 32 (для вычисления N), то константа C3 должна быть увеличена на коэффициент 32.

Кроме того, на этапе 6 объяснения я отметил, что новая техника с использованием shift увеличивает производительность конкретно на компьютерах с x64, и не должна влиять на устройства с ARM. Проведя тестирование, я выяснил, что эта оптимизация отрицательно влияет на производительность на Apple M4 Pro, предположительно из-за потери какой-то параллелизации. Поэтому я рекомендую применять проверку во время компиляции, чтобы ограничить это улучшение только устройствами с x64.

Применение описанных выше изменений приводит к следующим изменениям в алгоритме:

• Примечание: выделенные зелёным части упрощаются на этапе компиляции.

Улучшение для ARM64 / Apple Silicon

Точность и диапазон

К счастью, диапазон точных значений для алгоритма очень широк:

Первая дата выше этого диапазона приведёт к переполнению. Первая дата ниже этого диапазона некорректно вернёт 29 февраля в невисокосном году.

64-битное время UNIX (в секундах) покрывает диапазон примерно 585 миллиардов лет, а мой алгоритм точен в диапазоне триллионов лет, поэтому его достаточно для обработки полного диапазона 64-битного времени UNIX.

Хоть я и не создал формального доказательства для этого диапазона, в кодовой базе бенчмарка есть тестовый случай, верифицирующий указанный выше диапазон. Проверять весь диапазон было бы слишком долго (примерно месяц на Apple M4 Pro), поэтому сначала он выполняет такие быстрые проверки:

• [-232 ... 232]

• [MAX_DATE − 232 ... MAX_DATE]

• [MIN_DATE ... MIN_DATE + 232]

• Случайную выборку из дат 232

Портируемость

Так как алгоритм только 64-битный, разработчики библиотек могут заинтересоваться его безопасным развёртыванием с портированием, поддерживающим 32-битные компьютеры.

Быстрые 32-битные алгоритмы из статьи 1 (самый быстрый) и статьи 2 (безопасный на всём диапазоне 32-битных входных данных) были дополнены техниками из этого алгоритма. Теперь они заметно быстрее, чем в соответствующих статьях.

• Обновлённый более быстрый 32-битный алгоритм

• Обновлённый более быстрый алгоритм для всего 32-битного диапазонаBit Wide-Input algorithm

Если вашему API нужна поддержка только ограниченного диапазона из примерно 2³⁰ дней (~1 миллиарда дней / ~2,9 миллиона лет), то для каждого типа платформы самой быстрой из известных будет следующая комбинация:

• Этот алгоритм для 64-битных компьютеров

• Мой алгоритм из статьи 1 для 32-битных компьютеров

Если вы предпочитаете, чтобы API обрабатывал даты в полном диапазоне 32-битных значений (часто это оказывается наилучшим выбором), то вам подойдёт следующая комбинация:

• Этот алгоритм для 64-битных компьютеров

• Мой алгоритм из статьи 2 для 32-битных компьютеров.

Мой алгоритм из статьи 2 — это единственный известный мне быстрый алгоритм 32-битных дат, на 100% защищённый от переполнения в диапазоне 32-битных входных значений. Он и защищён от переполнений, и очень быстр; быстрее, чем Boost, но, в зависимости от устройства, или медленнее, или быстрее, чем Neri-Schneider. Стоит отметить, что Boost и Neri-Schneider поддерживают только примерно 25% от диапазона 32-битных значений.

Этот защищённый от переполнения алгоритм был создан исключительно для поддержки описанного выше сценария.

Результаты бенчмарков

Код бенчмарков — это прямой форк бенчмарков Neri‑Schneider (GitHub). Относительное соотношение скоростей вычислено с предварительным вычитанием производительности scan; это устраняет оверхед вызова функции из бенчмарка, что также применяется в Neri‑Schneider.

Чем ниже значения, тем быстрее

Перечисленные в таблице платформы были выбраны, потому что они создают стабильные, согласованные результаты, соответствующие ожиданиям. Также я протестировал алгоритм на Lenovo IdeaPad Slim 5 (Snapdragon ARM64), но он показал рост скорости на 60%. Это указывает на то, что тепловыделение или управление питанием искажает поведение коротких циклов бенчмарков. Аналогично, MacBook Pro на x86 (2016 года и 2020 года) показывали рост скорости всего на 2–10%, а другие алгоритмы были вдвое медленнее ожидаемого. Это тоже указывает на то, что CPU применяет агрессивную оптимизацию для экономии заряда аккумулятора или снижения тепловыделения, из-за чего результаты становятся ненадёжными.