Использование случайных битов — один из способов усиления возможностей компьютеров. Вероятностные алгоритмы позволяют решать некоторые задачи теоретической информатики, для которых не работают детерминированные алгоритмы. Самый интересный вопрос — это насколько использование случайностей сокращает время работы алгоритма? Частично на этот вопрос уже можно ответить: при некоторых предположениях истинную случайность можно подменить фальшивой и детерминированно смоделировать любой вероятностный алгоритм с незначительной потерей во времени работы. Проверка этих предположений будет, по всей видимости, одной из центральных тем теоретической информатики XXI века.
Лекцию читает старший научный сотрудник Вычислительного центра им. А.А. Дородницына РАН, доцент кафедры математических основ управления МФТИ, кандидат физико-математических наук Михаил Вялый.
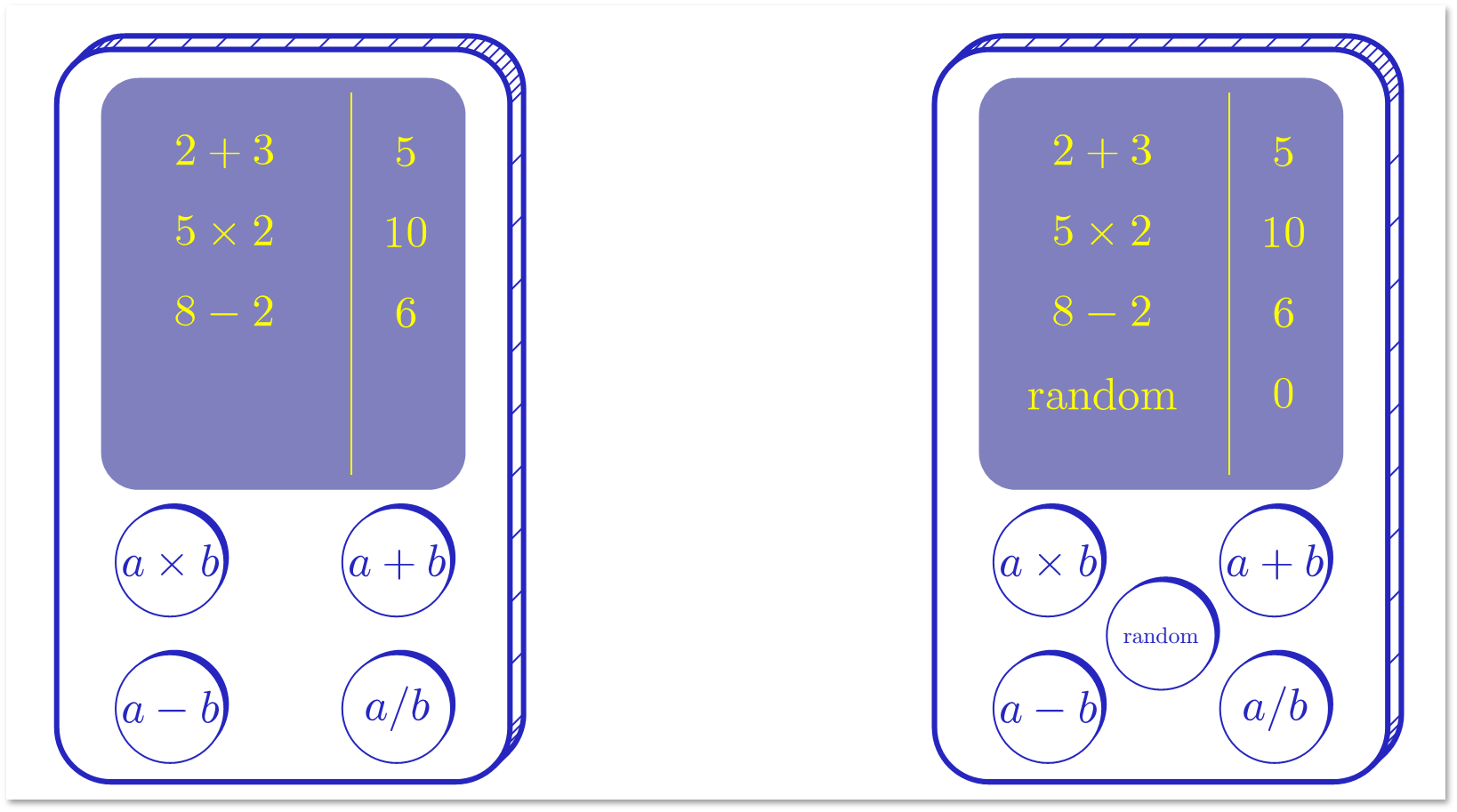
Представим, что у нас есть два калькулятора. Один обычный, а у второго есть дополнительная кнопка, которая при нажатии выдает дополнительный бит. Попробуем ответить на вопрос, полезна ли будет такая функция?
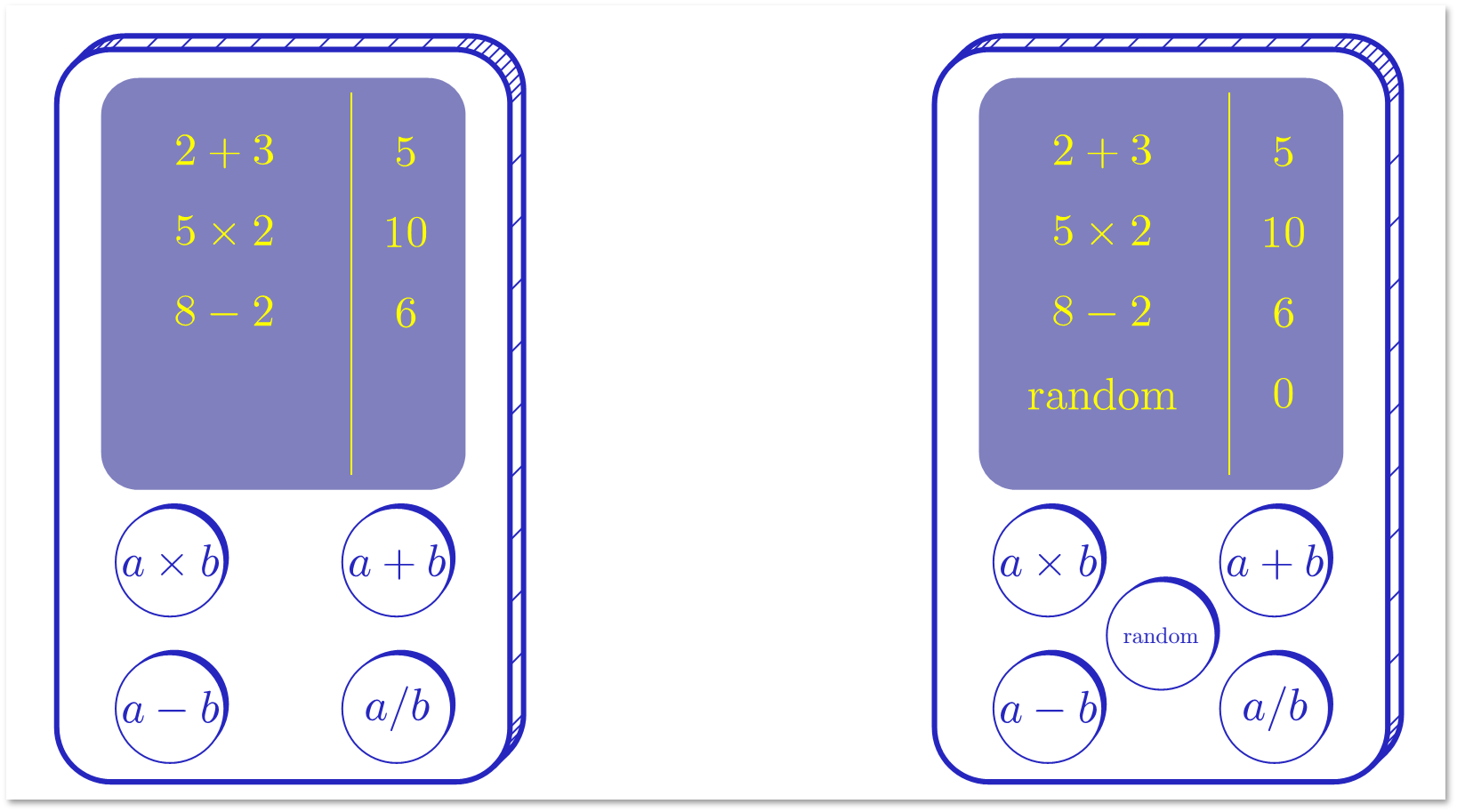
Такая постановка, конечно, слишком общая. Постараемся уточнить ее с точки зрения теоретической информатики. Для этого сначала введем понятие алгоритма. Алгоритм — настолько точно определенная инструкция, что она может быть исполнена механически. Основное свойство детерминированных алгоритмов заключается в том, что каждое следующее состояние однозначно определяется текущим состоянием. Вероятностные алгоритмы отличаются тем, что в любой момент они могут определить значение случайного бита (подбросить монету), который с равной вероятностью будет равен 0 или 1. В процессе исполнения вероятностного алгоритма это может происходить неоднократно, и разные подбрасывания будут независимы.
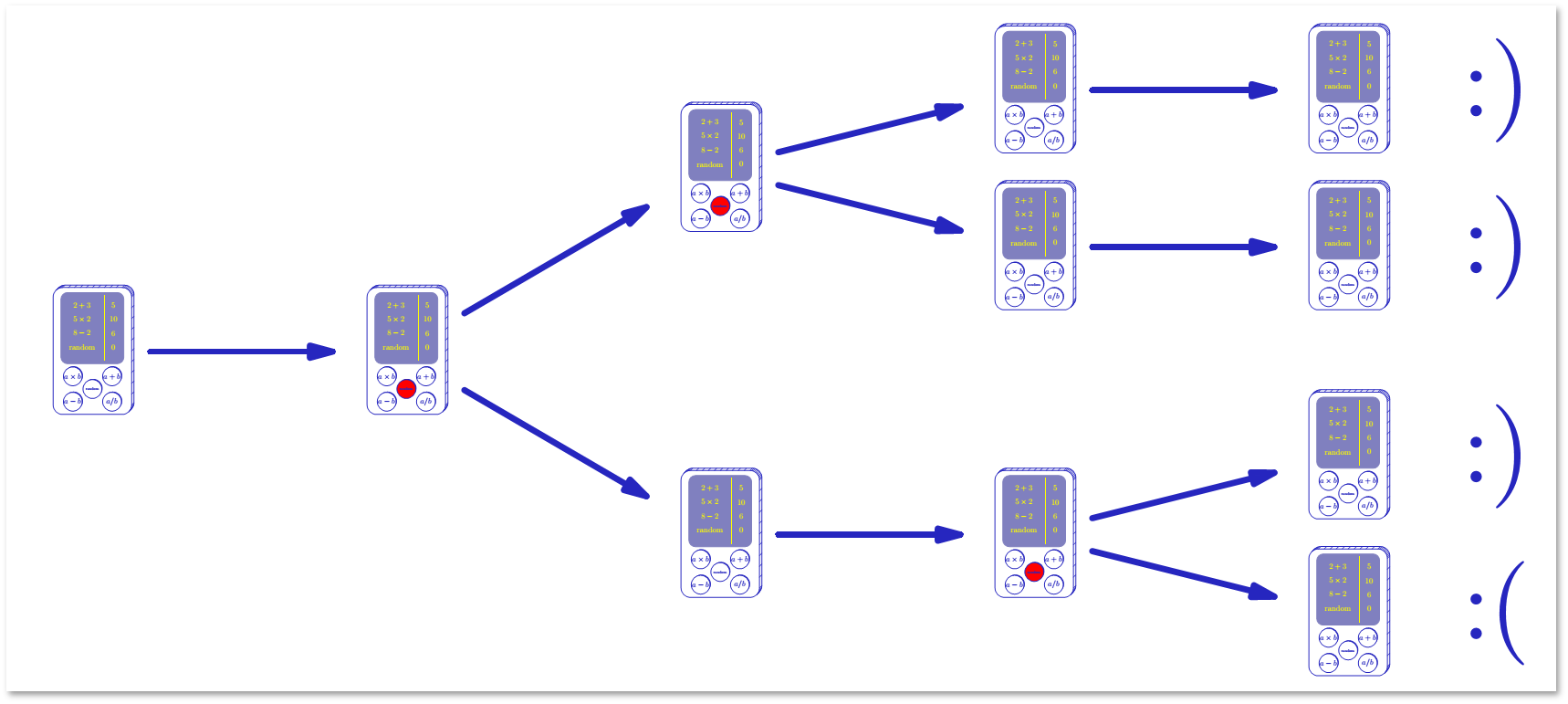
Как изображено на картинке выше, при детерминированном шаге, вычисления происходят как обычно. Однако при подбрасывании монетки вычисление разветвляется. Вместо линейной последовательности получается дерево вычисления. Каждая ветвь этого дерева называется путем вычисления. Путь характеризуется значениями случайных битов. Каждый раз, подбрасывая монетку, мы выбираем одно из двух направлений движения. Таким образом, мы допускаем некоторую вольность: разрешаем, чтобы алгоритм корректно работал не на всех путях, а только на некоторых. Прежде чем переходить к оценке возможностей ошибки вероятностных алгоритмов, оговорим некоторые технические детали.
Во-первых, у подбрасываемой монетки может быть много сторон (исходов). Во-вторых, вероятности выпадения всех возможных исходов не обязательно должны быть равны. Однако сумма всех возможных исходов всегда равна 1.
Подсчет вероятности ошибки
При подсчете вероятности ошибки вероятностного алгоритма нужно учитывать два правила:
- Вероятности независимых событий перемножаются.
- Вероятности несовместных событий складываются.
Как вообще относиться к алгоритмам, которые могут ошибаться? В конце концов, можно просто задать, какой-нибудь вопрос, требующий ответа «да»/«нет», подбросить двустороннюю монетку, и с вероятностью 1/2 получить верный ответ. Так какая же вероятность ошибки нас устроит? Например, велика ли вероятность ошибки в 9/10? Если ошибку можно обнаружить, и алгоритм допускает повторное исполнение, то не очень.

Если правильный ответ нам неизвестен, задача становится сложнее. Алгоритм дает нам ответ «да» или «нет». Если вероятность ошибки ε < 1/2, то повторения алгоритма позволяют быстро уменьшать вероятность ошибки. Т.е. нужно повторить алгоритм k раз, и выдать тот ответ, который встретился чаще. Пусть вероятность ошибки равна 1/3. Вероятность ошибки при голосовании k независимых исполнений вычисляется следующим образом:
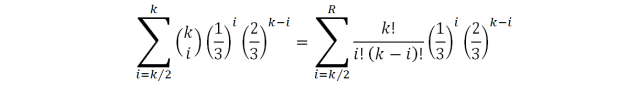
Если вероятность ошибки также равна 1/3, при голосовании 100 независимых исполнений вероятность ошибки можно вычислить так:
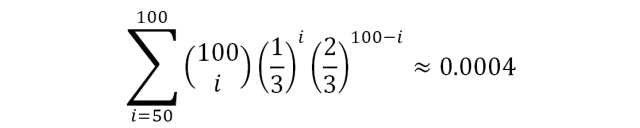
С повышением значения k вероятность ошибки будет очень быстро уменьшаться:
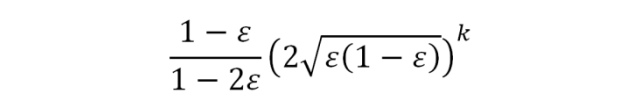
Задача об установлении контакта
Допустим, у нас есть два игрока. Они ничего не знают друг о друге, и возможности договориться у них нет. Есть две точки, через которые они могут установить контакт. Время дискретно. В каждый момент участник выбирает место (верхнее или нижнее). Контакт установлен, если в какой-то момент времени оба участника выбрали одно и то же место.
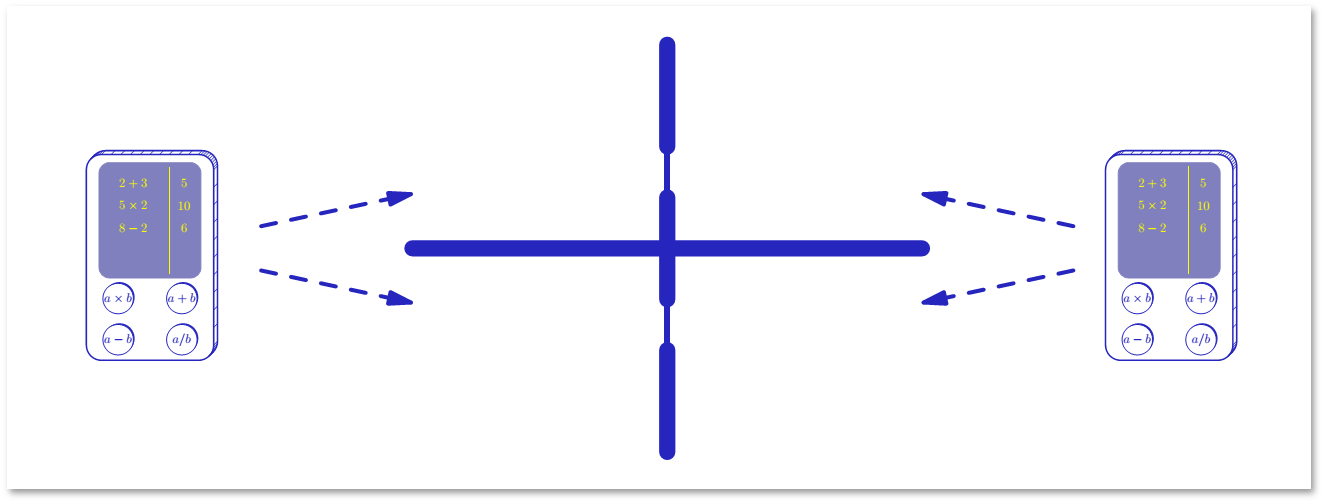
Детерминированного способа, позволяющего установить контакт, не существует. При этом вероятностный алгоритм для установления контакта очень прост: на каждом шаге нужно выбирать место случайно, равновероятно и независимо от предыдущих шагов. Проанализируем этот алгоритм. Вероятность ошибки на каждом шаге составляет 1/2. После t шагов вероятность ошибки будет составлять 2-t, что может быть очень маленькой величиной.
Задача проверки равенства третейским судьей
Рассмотрим задачу с более сложным условием. Алиса знает двоичное слово x длины n. Боб знает слово y той же длины. Они имеют возможность передать Чарли некоторую информацию (слова u и v), по которой Чарли должен решить, равны ли слова x и y. Цель: передать как можно меньше битов при условии, что Чарли правильно отвечает на любых x, y. Алиса с Бобом друг с другом общаться не могут.
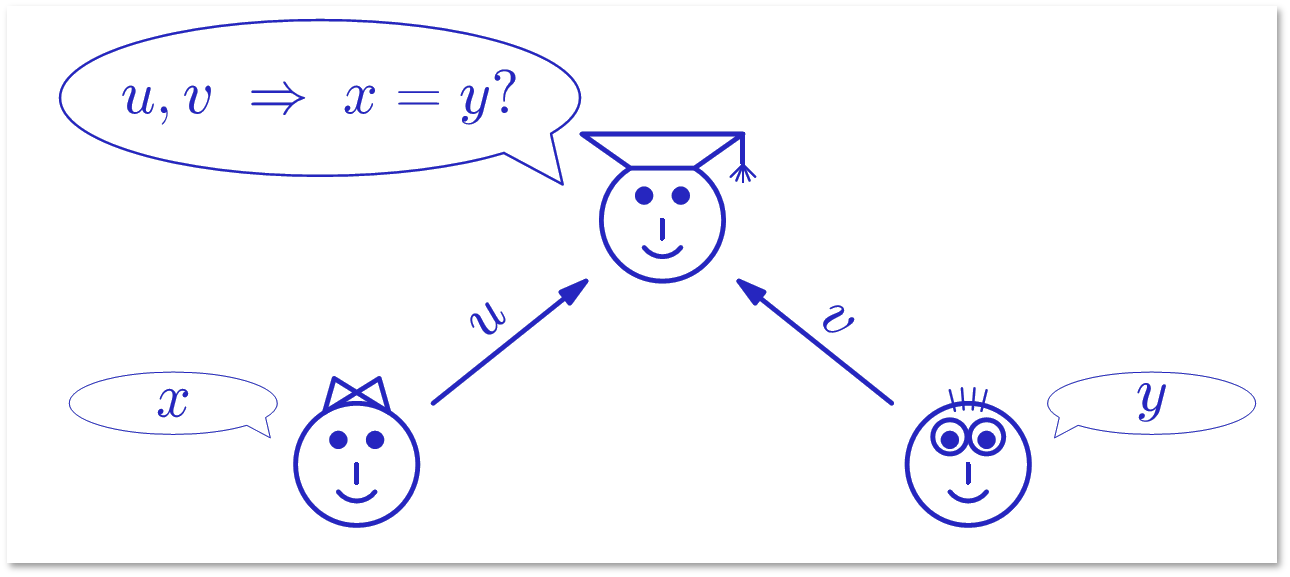
Если u и v определяются по x и y детерминированно, т.е. u = f (x), v = g (y), то для решения задачи равенства нужно передать не меньше 2n битов. Путь длина u меньше n. Тогда возможных значений u меньше 2n, т.е. меньше количества возможных значений x.
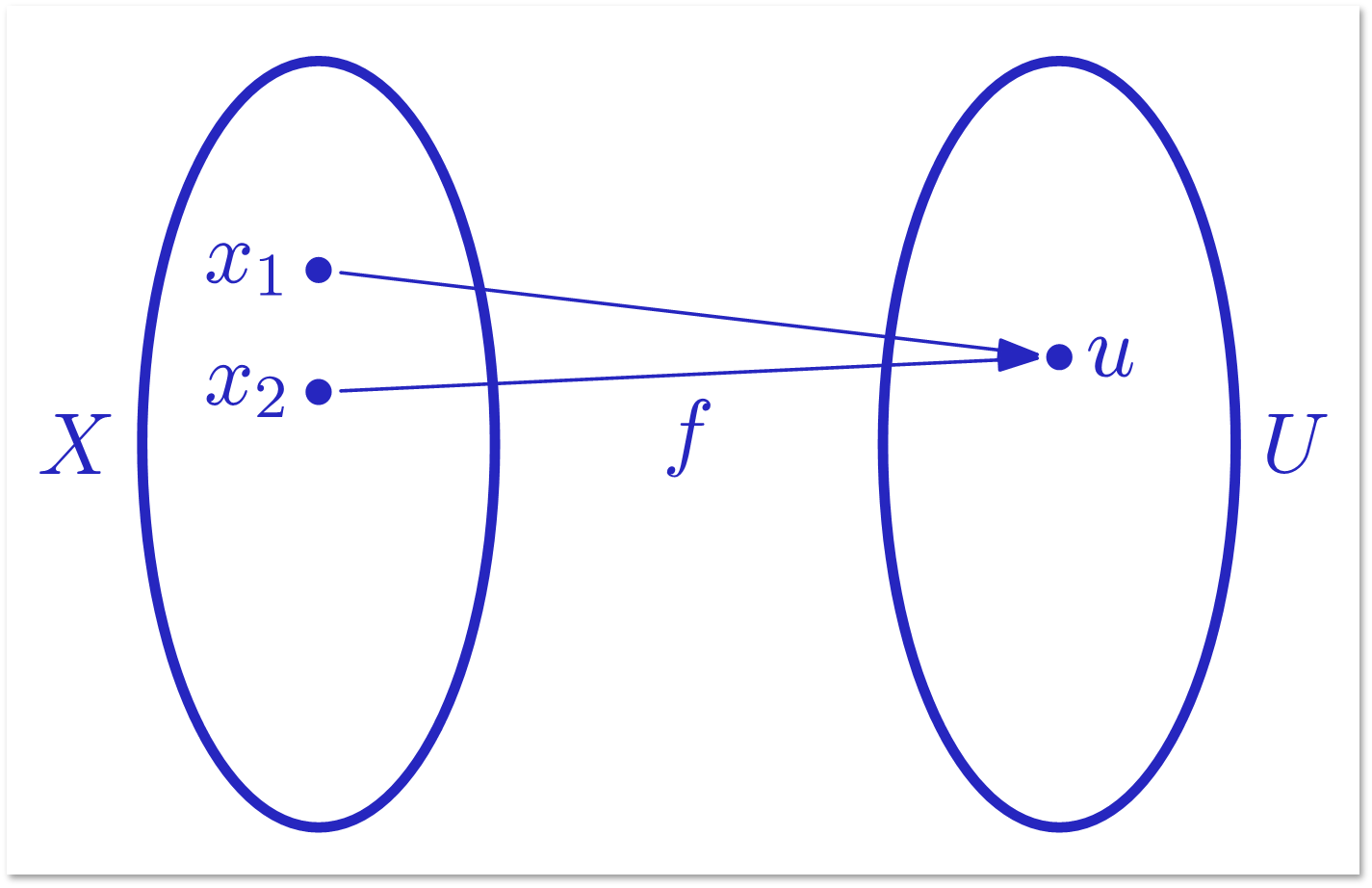
Для Чарли x1 и x2 неразличимы.
Случайность как «канал связи»
Попробуем решить туже задачу, но теперь представим, что Алиса и Боб имеют доступ к общему источнику случайности. Скажем, к одному и тому же изданию книги «Таблица случайных чисел». Цель: передать как можно меньше битов при условии, что вероятность ошибки Чарли мала на любых x, y.
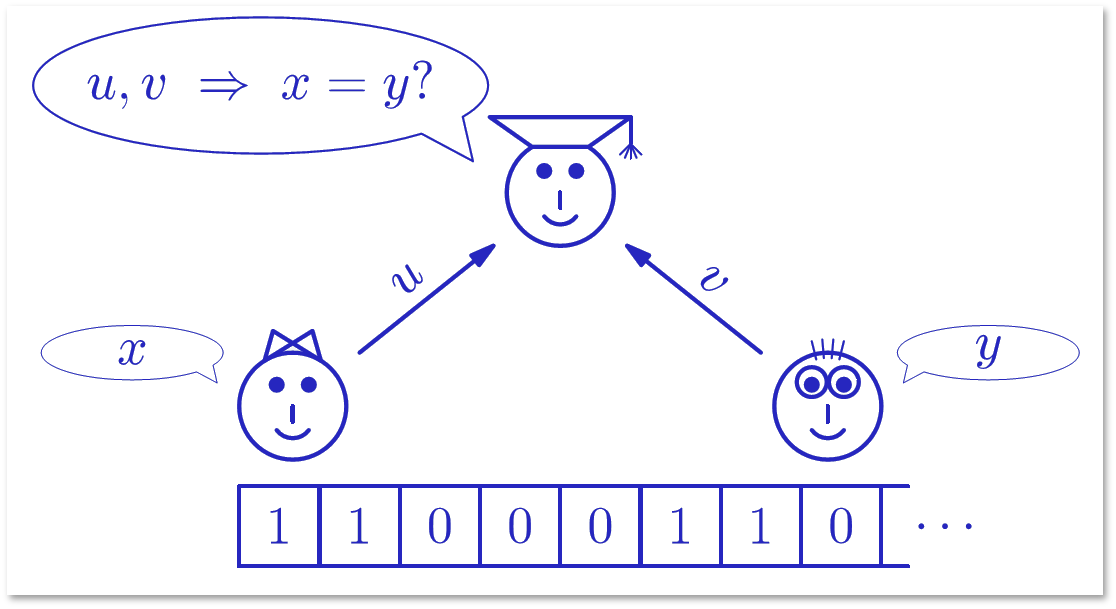
Попробуем решить эту задачу и определить, можно ли таким образом передавать меньше битов, чем с помощью детерминированного алгоритма.
Алиса и Боб выбирают случайное простое число p (одно и то же, случайность общая для них обоих) в интервале от n до 2n.
Алиса вычисляет U = X mod p, где X – число, двоичная запись которого совпадает со словом Алисы x. Боб поступает аналогично и вычисляет V = Y mod p. Затем они оба посылают двоичные записи чисел U и V Чарли. Чарли говорит, что слова x и y равны, если u = v.
Поскольку 0 ≤ U, V < p ≤ 2n, то длина сообщений ≤ 2 + log n.
В случае x = y Чарли всегда дает правильный ответ. Если x≠y вероятность ошибки Чарли не больше 3/4. Докажем это с помощью теоремы из теории чисел.
Простых чисел довольно много. Для всех достаточно больших n количество π(n) простых чисел от 1 до n удовлетворяет неравенствам:
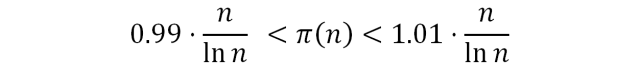
Если X — Y ≠ 0 делится на простые n ≤ p1 <… < pk ≤ 2n, то
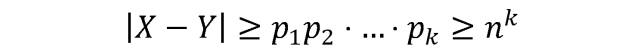
Уменьшение вероятности ошибки
Ошибка предложенного протокола — односторонняя. Это позволяет уменьшать вероятность ошибки путем многократного выполнения протокола. Если Алиса и Боб выбирают s простых модулей (случайно и независимо), вероятность ошибки становится меньше (3/4)s. Взяв достаточно большое s, вероятность ошибки можно сделать сколь угодно малой.
При наличии общей случайности для любого ε > 0 существует такой способ выбора сообщений, который гарантирует решение задачи равенства с вероятностью ошибки меньше ε и передает O(log n) битов. Запись g (n) = O(f(n)) означает, что есть такие числа C и n0, что для всех n > n0 выполняется g(n) < Cf(n).
Протоколы при отсутствии общей случайности
Как доказать, что есть способ выбора сообщений u, v в задаче равенства, при котором Алиса и Боб не знают случайных битов друг друга, передается O(√n log n) битов, а вероятность ошибки меньше 1/3?
Два случайных подмножества размера 2√n в n-элементном множестве пересекаются с вероятностью > 4/5 (примерно 1 − 1/e2). И оказывается, что это почти все, чего мы можем достичь. Рассмотрим частный случай теоремы Бабаи – Киммеля, из которой следует, что при любом способе вероятностного выбора сообщений в задаче равенства, гарантирующем вероятность ошибки меньше 1/3, длина переданных сообщений Ω(√n). Запись g(n) = Ω(f(n)) означает, что есть такие числа C и n0, что для всех n > n0 выполняется g(n) > Cf(n).
Посмотрев лекцию до конца, вы узнаете, как благодаря внедрению случайности можно ускорять работу алгоритма, а также о понятии фальшивой случайности.
Автор: elcoyot






