Добрый день. На первом курсе бакалавриата Академического университета читается годовой курс алгоритмов. Каждая лекция сопровождается семинаром, на котором мы разбираем алгоритмические задачи. Практические семинары проходят в небольших группах. В этом семестре я читаю лекции и веду практику у одной из групп.
Сегодня хочу поделиться с Вами двумя задачами с этих семинаров.
Задача 1. На прямой даны n отрезков, нужно выбрать максимальное по размеру подмножество непересекающихся.
Задача 2. На окружности даны n дуг (отрезков), нужно выбрать максимальное по размеру подмножество непересекающихся.
Первая задача — один из примеров на тему «жадные алгоритмы». Решение можно посмотреть внизу. Если коротко, предполагается решение сортировкой за O(sort+n). Здесь за sort я обозначаю время на сортировку массива длины n. Кстати, sort — необязательно nlogn (например, bucket sort, radix sort, входные данные из ограниченного диапазона).
Вторая задача имеет красивое вероятностное решение за O(sort+n). Не смотря на свою похожесть на первую, вторая задача в лоб жадностью не решается. Вернее лично мне неизвестно жадное решение, если кто-нибудь из читателей придумает и поделится, буду рад послушать. А чтобы проще было думать, я сразу опишу несколько неработающих идей, наиболее часто всплывающих при попытках решать эту задачу:
- Пусть на окружности есть точка, не покрытая ни одним отрезком, тогда окружность можно разрезать в этой точке и получить задачу про прямую, которую мы уже умеем решать!
Да. Но таких точек может не быть. Более того, каждая точка окружности может быть покрыта 2, 10, или даже Θ(n) отрезками - Разрезать окружность по точке, покрытой минимальным количеством отрезков!
Не работает. Представьте себе 3 разбиения окружности на 10 отрезков. Всего 30 отрезков. В двух из этих «разбиений» отрезки слегка накладываются друг на друга. Нам нужно угадать третье из разбиений и точкой разреза выбрать конец одного из именно этих 10 отрезков. - Выгодно взять в ответ самый короткий отрезок!
Нет. Даже на прямой уже не правда: (0,49) (50,100) (48,51) - Выгодно выкинуть из множества самый длинный отрезок, который кого-нибудь пересекает!
Нет. Смотрите предыдущий пример. - А ещё...
Есть много неработающих идей, остановим перечисление на уже озвученных.
Решения задач
Решение задачи 1.
У каждого отрезка i есть левый конец L[i] и правый конец R[i]. Отсортируем отрезки в порядке возрастания R[i]. В таком порядке будем перебирать отрезки. Очередной отрезок будем добавлять в ответ, если его левая граница больше максимума правых границ уже добавленных отрезков.
Решение задачи 2.
Предупреждаю, решение длинное и гораздо сложнее предыдущего. С другой стороны принципиально сложных идей тут нет, так что всё можно понять без начальной подготовки.
Для начала скажем, как задаются дуги на окружности. Пусть окружность — зацикленный отрезок [0..M), а дуги (отрезки) окружности задаются парами L[i]..R[i]. Если R[i] < L[i], отрезок проходит через точку M.
Основная идея решения — найти точку, в которой можно разрезать окружность. Вернее так: выбрать отрезок i, который мы точно возьмём в ответ. Как только такой отрезок i зафиксирован, окружность можно разрезать, например в точке R[i].
Представляя все объекты на окружности, решать задачу не очень удобно. Поэтому, используя приём «удвоение окружности», перейдём на прямую.
1. Если у какого-то отрезка R[i] < L[i], то сделаем R[i] += M.
2. Для любого отрезка L[i]..R[i] породим парный ему L[i]+M..R[i]+M
Теперь у нас есть 2n отрезков на прямой, а окружность с разрезом в точке x соответствует отрезок этой прямой [x..x+M), где 0 <= x < M.
Решение задачи 2 за O(sort + n2). Отсортировать один раз отрезки по правому концу, затем перебрать n возможных точек разреза R[i], решая для каждой задачу за O(n), так же как Задачу 1.
Решение задачи 2 за O(sort + nk), где k — размер множества-ответа на задачу. Оставим сортировку.
А сразу после сортировки воспользуемся методом двух указателей и за O(n) для каждого отрезка i насчитаем следующий отрезок next[i], который мы бы взяли нашей жадностью (жадность: L[next[i]] > R[i], из таких next[i] = min).
// Код метода двух указателей
b = 0;
for (a = 0; a < n; a++) {
while (L[b] <= R[a]) b++; // за всё время b увеличится не более 2n раз
next[a] = b;
}Теперь сделаем интересное наблюдение: в зависимости от точки разреза размер полученного нами множества отличается от оптимального не более чем на 1. То есть, если мы разрезали в первой попавшейся точки и получили множество размера k, нам достаточно найти множество размера k-1, и оно точно будет оптимальным.
Решение: перебираем первый отрезок, делаем k-2 шагов вперёд с помощью ссылок next, если расстояние между самой правой и самой левой точкой меньше M, мы нашли k-1 непересекающихся дуг.
for (a = 0; a < n; a++) {
b = a;
for (i = 0; i < k - 2; i++) b = next[b];
if (R[b] - L[a] < M) ; // Успех, нашли k-1 отрезков! Это a, next[a], next[next[a]] ... b
}
Решение за O(sort + n)
Возьмём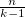 
раз случайную точку i = random [0..n-1]. Для каждого i за O(k) попробуем a = next[i], как в коде выше.
Поскольку, если ответ из k-1 отрезков существует, нам достаточно было попасть в какой-то один из этих k-1, то вероятность того, что за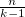 
попыток мы ни разу не попали равна 
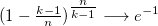при 
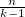стремящимся к бесконечности. Заметим, что если 
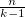= Θ(1), то предыдущий алгоритм за O(nk) нас полностью устраивал. Т.е. мы получили вероятностный алгоритм, время работы которого O(sort + n). Чтобы достигнуть лучшей ошибки e-T, достаточно попробовать не 
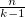, а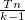 
точек, время работы соответственно будет O(sort + Tn).
Эпилог
Не всегда на определённую тему достаточно уже готовых задач, регулярно приходится придумывать новые. Только что мы наблюдали забавный эффект: берём классическую простую задачу на сортировку, заменяем «прямую» на «окружность», получаем сложную задачу на метод двух указателей и вероятностную идею. Многие красивые учебные задачи так и придумываются. Кстати, попробуйте решить ещё две задачи:
Задача 3. Даны n отрезков на прямой, выбрать максимальное по размеру подмножество отрезков такое, что каждая точка покрыта не более чем k раз (мы её только что решали для k=1).
Задача 4. Даны n дуг (отрезков) на окружности… и та же самая задача.
Ещё больше задач
Если задачи Вам понравились, по ссылкам осень и весна можно найти ещё порядка сотни задач за осенний и весенний семестр этого года. К некоторым задачам прилагается разбор.
Автор: Burunduk1
