Аннотация
Данная статья содержит описание метода графического тестирования случайных последовательностей, на соответствия критериям истинно случайным последовательностям. В статье приводиться обзор метода «Приблизительной энтропии» входящего в состав пакета тестирования NIST, также приводятся сравнительный анализ последовательностей полученных при помощи ГПСЧ описанных в статье Ocelot Генерация случайных чисел на микроконтроллерах
Тест «Приблизительной энтропии»
Расчет «Приблизительной энтропии» (Approximate Entropy) является одним из тестов входящих в состав пакета тестирования NIST.
Данный тест заключается в подсчете частоты всех возможных перекрываний шаблонов длины m бит на протяжении исходной последовательности битов. Цель теста — сравнить частоты перекрывания двух последовательных блоков исходной последовательности с длинами m и m+1 с частотами перекрывания аналогичных блоков в абсолютно случайной последовательности. Вычисляемое в ходе теста значение вероятности p должно быть не меньше 0,01. В противном случае (p < 0,01), двоичная последовательность не является абсолютно произвольной.
ApEn(m), где n — длина в битах входящей последовательности; m — длина в битах начального блока для тестирования; ε — битовая последовательность
Шаг 1
Дополните n-битовую последовательность чтобы получилось ровно n перекрытий m-битной последовательностью. Для этого добавьте m-1 бит из начала последовательности в ее конец.
Например: ε = 0100110101 и m = 3, тогда n = 10. Добавляем 0 и 1 в начало последовательности и в конец последовательности. (Это делается для каждого значения m).
Получится тестовая последовательность: 010011010101.
Шаг 2
Частота рассчитывается для n перекрывающихся блоков (например: если блок содержащий εj и εj+m-1 рассчитывается в позиции j, тогда блок содержащий εj+1 и εj +m рассчитывается в позиции j+1).
Пусть количество возможных m-bit ((m+1)-bit) значений будет представлено как Cmi, где i есть m-битное значение.
Для тестовой последовательности полученной на 1 шаге, перекрывающие m-битные блоки (при m = 3) будут 010, 100, 001, 011, 110, 101, 010, 101, 010, and 101. Количество вхождений 2m = 23 = 8 м-битовых последовательностей:
#000 = 0, #001 = 1, #010 = 3, #011 = 1, #100 = 1, #101 = 3, #110 = 1, #111 = 0
Шаг 3
Производим расчет Cmi для каждого значения i.
C3000 = 0, C3001 = 0.1, C3010 = 0.3, C3011 = 0.1, C3100 = 0.1, C3101 = 0.3, C3110 = 0.1, C3111 = 0.
Шаг 4
Производим расчет
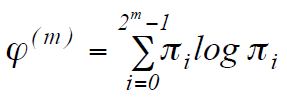
Шаг 5
Повторяем шаги 1-4 для m = m + 1
Шаг 6
Получаем значение ApEn(m) = φ(m)-φ(m+1)
Для текущего примера ApEn(3) = -1.643418 – (-1.834372) = 0.190954
Входящие значения
Необходимо выбирать значения n и m такие чтобы: m < log2n-5
Построение графиков
Для получения графиков были проведены серии тестов по расчету ApEn при m=2. Значение n изменялось в диапазоне от 0 до 1000000 c шагом 100. Были также проведены серии тестов с шагом 1. Полученные результаты с шагом 1 и шагом 100 значительных отличий не имеют, поэтому тестирования проводилось именно с шагом 100. Примерное время расчета одной последовательности длинной в 1000000 бит занимает около 7 минут на Intel Core i3 U380 1,33 GHz в один поток, и около 6:30 минут в 16 потоков. Для отображения графиков используется логарифмическая шкала Y, а также результаты представлены в виде отклонения от нормального распределения. Принцип расчета описан в статье STEVEN M. PINCUS Approximate entropy as a measure of system complexity
Графическое представление результатов
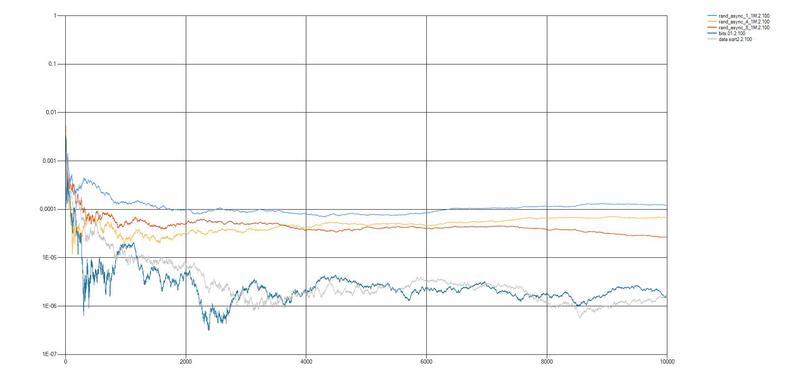
1. Источник энтропии на асинхронных таймерах
Таймер 1 — watchdog, тактирование от RC-генератора, период T1 = 15 мс.
Таймер 2 — 8 битный, тактирование от кварцевого генератора, тактовая частота F = 16.0 МГц.
rand_async_1_1M — в качестве результата использован 1 младший бит счетчика 2. Скорость генерации 120 бит/с
rand_async_4_1M — в качестве результата использованы 4 младших бита счетчика 2. Скорость генерации 280 бит/с
rand_async_8_1M — в качестве результата использованы все 8 бит счетчика 2. Скорость генерации 450 бит/с
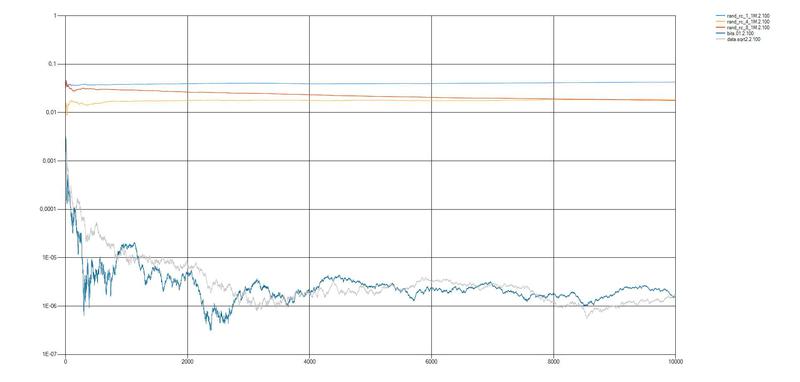
2. Источник энтропии с RC-цепью
Постоянная времени RC = 5 мс. Тактовая частота счетчика F = 16.0 МГц.
rand_rc_1_1M — в качестве результата использован 1 младший бит счетчика. Скорость генерации 370 бит/с
rand_rc_4_1M — в качестве результата использованы 4 младших бита счетчика. Скорость генерации 1500 бит/с
rand_rc_8_1M — в качестве результата использованы все 8 бит счетчика. Скорость генерации 2870 бит/с
3. Источник энтропии на АЦП
Измеряемое напряжение VDD = 3.3 В (нестабилизированное), опорное напряжение VCC = 5.0 В. Разрядность АЦП 10 бит, тактовая частота преобразования 125 кГц.
rand_adc_1_1M — в качестве результата использован 1 младший бит результата АЦП. Скорость генерации 8.93 кбит/с
rand_adc_2_1M — в качестве результата использованы 2 младших бита результата АЦП. Скорость генерации 17.9 кбит/с
rand_adc_4_1M — в качестве результата использованы 4 младших бита результата АЦП. Скорость генерации 29.5 кбит/с

Заключение
Как мы видим из графического представления результатов анализ можно сделать выводы, что качество случайных последовательностей полученных при помощи микроконтроллеров, на несколько порядков меньше случайных последовательностей из набора DIEHARD и из последовательности полученной при извлечении квадратного корня из числа «2». Использование полученных случайных последовательностей в современной криптографии весьма опасна, что подтверждается также результатами тестов NIST и DIEHARD. Дальнейшим этапами исследования станут применение нераспространенных статистических тестов, для выявления истинно случайных последовательностей.
Автор: sleeplessaek






