В начале 2012 года по интернету гуляла видеозапись доклада Гарри Бернхардта на CodeMash под названием «WAT». На хабре были даже две хабрастатьи об этом докладе: раз, два. В этом выступлении рассказывалось про некоторые тонкости Ruby и JavaScript, которые кажутся нелогичными и вызывают реакцию: «WAT?».
В этой же хабрастатье я собрал десять примеров математических рассуждений, которые наоборот, на первый взгляд кажутся логичными, но видя полученный результат, также хочется задастся вопросом «ШТА?!!».
Итак, сможете определить где подвох?
1. Все в школе проходят формулу для суммы первых n членов арифметической прогрессии, применяя эту формулу к сумме первых n положительных целых чисел получаем:
1 + 2 + 3 + … + n = n(n + 1)/2.
Если же эту формулу применить к сумме чисел от 1 до n − 1, то получим конечно же
1 + 2 + 3 + … + (n − 1) = (n − 1)n/2.
Давайте к обеим частям последнего равенства прибавим по единице:
1 + 2 + 3 + … + (n − 1) + 1 = (n − 1)n/2 + 1.
Упрощая, получаем:
1 + 2 + 3 + … + n = (n − 1)n/2 + 1.
Чему равна сумма в левой части этого равенства мы записали в самом начале, следовательно,
n(n + 1)/2 = (n − 1)n/2 + 1.
Раскрываем скобки:
n2/2 + n/2 = n2/2 − n/2 + 1.
Упрощаем, и получаем, что
n = 1.
Так как n было произвольным, то мы показали, что все целые положительные числа равны 1.
1 + 2 + 3 + … + (n − 1) + 1 = 1 + 2 + 3 + … + n.
Это станет заметно, если вместо
1 + 2 + 3 + … + (n − 1)
написать
1 + 2 + 3 + … + (n − 3) + (n − 2) + (n − 1).
Тогда
1 + 2 + 3 + … + (n − 3) + (n − 2) + (n − 1) + 1 = 1 + 2 + 3 + … + (n − 3) + (n − 2) + n,
что конечно же не равно
1 + 2 + 3 + … + n.
2. Рассмотрим интеграл
.
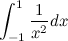Так как функция 1/x2 положительна на всей своей области определения, то значение интеграла должно быть положительным. Давайте проверим.
Первообразная функции 1/x2 может быть найдена в таблице первообразных и равна −1/x + const.
Воспользуемся формулой Ньютона-Лейбница:
.
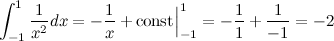3. Рассмотрим систему уравнений
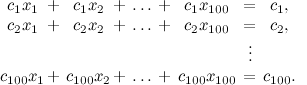
Число переменных совпадает с числом уравнений, поэтому применим метод Крамера, который заключается в том, что решение выражается в виде xk = Δk / Δ, где Δ — определитель матрицы системы, а Δk — определитель матрицы, полученной из матрицы системы заменой k-го столбца на столбец свободных членов. Но столбец свободных членов совпадает с любым из столбцом матрицы, поэтому Δ = Δk. А значит, xk = 1 для всех k. Хорошо, подставим это решение в первое уравнение:
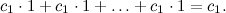
Следовательно, 100c1 = c1. Деля обе части равенства на c1, получаем, что 100 = 1.
4. Рассмотрим ряд
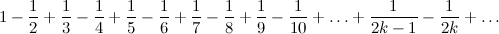
Это так называемый знакопеременный гармонический ряд, он сходится, и его сумма равна ln 2.
Переставим члены этого ряда так, чтобы за одним положительным членом следовали два отрицательных:
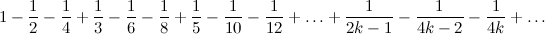
Вроде бы ничего страшного не произошло, ряд как сходился, так и сходится, но давайте рассмотрим подпоследовательность частичных сумм этого ряда:
.
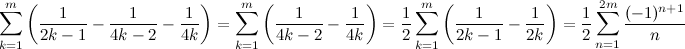Последняя сумма есть не что иное, как сумма первых 2m членов исходного знакопеременного гармонического ряда, сумма которого, как мы помним, равна ln 2. А это значит, что сумма ряда с переставленными членами равна ½ln 2.
5. Перейдём к пределам. Рассмотрим предел
.
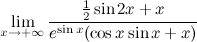Так как числитель и знаменатель стремятся к бесконечности при x стремящемся к бесконечности, а также числитель и знаменатель дифференцируемы, то можно применить правило Лопиталя.
Находим производную числителя:
(½sin2x + x)' = cos2x + 1 = 2cos2x.
Находим производную знаменателя:
(esinx(cosx sinx + x))' = esinxcosx(cosx sinx + x) + esinx(−sin2x + cos2x + 1) = esinxcosx(cosx sinx + x + 2cosx).
Откуда
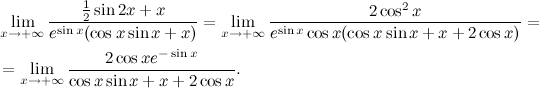
Теперь замечаем, что числитель является ограниченной функцией, а знаменатель стремится к плюс бесконечности при стремлении x к плюс бесконечности, поэтому предел равен 0.
Если вы не заметили ничего необычного, то давайте в исходном пределе знаменатель перепишем следующим образом:
esinx(cosx sinx + x) = esinx(½sin2x + x).
Поэтому числитель и знаменатель исходной функции можно просто сократить на ½sin2x + x, следовательно, функция под знаком предела просто равна e−sinx. А такая функция уже предела не имеет при x стремящемся к плюс бесконечности!
Данный пример я взял из диссертации D. Gruntz «On Computing Limits in a Symbolic Manipulation System».
6. Вот ещё один предел:
.
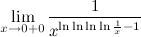Давайте посмотрим на график функции под знаком предела:
(%i14) plot2d(1/x^(log(log(log(log(1/x)))) - 1), [x, 0, 0.01]);
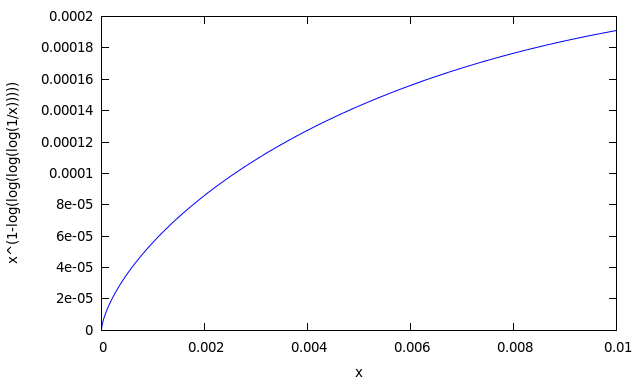
Видно, что функция при x стремящемся к нулю справа стремится к нулю. Давайте посчитаем для уверенности несколько значений:
(%i47) f(x) := 1/x^(log(log(log(log(1/x)))) - 1)$
(%i48) f(0.00001);
(%o48) 2.7321447178155322E-6
(%i49) f(0.0000000000000001);
(%o49) 9.6464144195334194E-13
(%i50) f(10.0^-20);
(%o50) 7.8557909648538576E-15
(%i51) f(10.0^-30);
(%o51) 1.0252378366509659E-19
(%i52) f(10.0^-40);
(%o52) 2.8974935848725609E-24
(%i53) f(10.0^-50);
(%o53) 1.4064426717966528E-28
Так что предел наверняка равен 0. Согласны? Посчитаем символьно:
(%i59) limit(1/x^(log(log(log(log(1/x)))) - 1), x, 0, plus);
(%o59) inf
Получили плюс бесконечность! И это правильный ответ.
Этот пример я также взял из диссертации D. Gruntz «On Computing Limits in a Symbolic Manipulation System».
7. Рассмотрим матрицу
.
Воспользуемся каким-нибудь математическим пакетом, чтобы найти её собственные числа. У меня под рукой была Maxima, поэтому я воспользовался ей:
(%i162) load(lapack)$
(%i163) dgeev(C);
(%o163) [[1.892759249004818 %i + 5.064646369950517,
5.064646369950517 - 1.892759249004818 %i,
4.316308825205465 %i + 1.156345532561647,
1.156345532561647 - 4.316308825205465 %i, - 5.560325596213962,
3.327556714595323 %i - 3.440829104405306,
- 3.327556714595323 %i - 3.440829104405306], false, false]
То есть получили примерно такие собственные числа:
−5,560, 5,064 + 1,892i, 5,064 − 1,892i, 1,156 + 4,316i, 1,156 − 4,316i, −3,440 + 3,327i, −3,440 − 3,327i.
Хорошо, числа как числа, но давайте ещё найдём собственные числа транспонированной матрицы, мы ожидаем получить те же самые числа, так как собственные числа у матрицы при транспонировании не меняются.
(%i164) dgeev(transpose(C));
(%o164) [[3.333252572558635 %i + 7.570309809213996,
7.570309809213996 - 3.333252572558635 %i,
7.453248893016916 %i + 1.804487379065658,
1.804487379065658 - 7.453248893016916 %i,
5.891112477041645 %i - 5.215502218450374,
- 5.891112477041645 %i - 5.215502218450374, - 8.318589939657096], false, false]
То есть собственные числа транспонированной матрицы примерно такие:
−8,318, 7,570 + 3,333i, 7,570 − 3,333i, 1,804 + 7,453i, 1,804 − 7,453i, −5,215 + 5,891i, −5,215 − 5,891i.
Ни одного совпадения! Но давайте пойдём дальше и найдём собственные числа символьно:
(%i166) eigenvalues(C);
(%o166) [[- 1, 1, - 2, 2, - 4, 4, 0], [1, 1, 1, 1, 1, 1, 1]]
В этот раз получили −1, 1, −2, 2, −4, 4, 0.
,
.
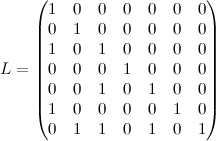Поэтому правильный ответ такой: −1, 1, −2, 2, −4, 4, 0.
Численные методы дают неправильные собственные числа, так как эта матрица является плохо обусловленной по отношению к задаче нахождения собственных чисел, и из-за погрешностей при вычислениях получается такая большая ошибка.
Подробнее про число обусловленности собственного значения можно прочитать, например, в книге Дж. Деммеля «Вычислительная линейная алгебра», отмечу только, что это число равно секансу острого угла между левым и правым собственным вектором данного собственного числа.
Данный пример с матрицей я взял из презентации С. К. Годунова «Парадоксы вычислительной линейной алгебры и спектральные портреты матриц».
8. Рассмотрим равенство, которые некоторые считают самым красивым в математике:
eiπ + 1 = 0.
Перепишем его в виде
eiπ = −1.
Возводя обе части равенства в квадрат, получим
e2iπ = 1.
А теперь возведём обе части последнего равенства в степень i:
(e2iπ)i = 1i.
Мы знаем, что 1 в любой степени равна 1, поэтому
e2i2π = 1.
Но также мы знаем, что i2 = −1, следовательно,
e−2π = 1.
Тут можно на всякий случай взять калькулятор и убедиться, что e−2π по-прежнему примерно равно 0,001867442731708, что уж точно не 1.
1i = {e−2πk | k ∈ Z}.
И поэтому чевёртый переход уже не является верным. Если же вы рассматриваем только одну из ветвей, то некоторые из привычных тождеств для степеней перестают выполняться, что здесь и произошло.
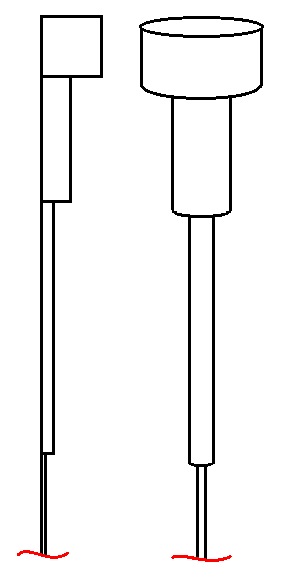9. Рассмотрим ступенчатую пластину бесконечной длины, состоящую из прямоугольников: первый прямоугольник — квадрат с размерами 1 см на 1 см, второй — прямоугольник с размерами 0,5 см на 2 см, каждый же следующий прямоугольник вдвое длиннее и в двое уже предыдущего, то есть имеет размеры 2k−1 на 21−k см. Заметим, что площадь каждого прямоугольника равна одному квадратному сантиметру, поэтому площадь всей пластины бесконечна. Следовательно, чтобы покрасить эту пластину потребуется бесконечное количество краски.
Рассмотрим сосуд, состоящий из цилиндров. Высота первого цилиндра равна 1 см, радиус равен также 1 см, высота второго цилиндра равна 2 см, радиус — 0,5 см, и так далее, каждый следующий цилиндр также в два раза длиннее предыдущего, а его радиус в два раза меньше.
Найдём объём этого сосуда: объёмы цилиндров образуют геометрическую прогрессию: π, ½π, ¼π, ..., π / 2k,… Поэтому суммарный объём конечен и равен 2π кубических сантиметров.
Заполним наш сосуд краской. Опустим в него нашу пластину и вытащим. Она будет полностью окрашена конечным количеством краски со всех сторон!
Когда мы рассуждали о невозможности покрасить пластину, мы предполагали, что пластина покрывается слоем краски одинаковой толщины.
При покраске же с помощью нашего сосуда, каждый следующий прямоугольник покрывается всё более тонким слоем краски.
10. Ну и напоследок докажем следующее утверждение:
Все лошади белого цвета.
Для доказательства воспользуемся индукцией.
База индукции. Очевидно, бывают лошади белого цвета. Выберем одну из таких лошадей.
Шаг индукции. Пусть доказано, что любые k лошадей белого цвета. Рассмотрим множество из k + 1 лошадей. Уберём из этого множества одну лошадь. Оставшиеся же k лошадей будут белого цвета по предположению индукции. Теперь вернём убранную лошадь и уберём какую-нибудь другую. Оставшиеся k лошадей снова будут белого цвета по предположению индукции. Следовательно, все k + 1 лошадей будут белого цвета.
Отсюда следует, что все лошади белого цвета. Что и требовалось доказать.
Если вы хотите ещё поискать ошибки в рассуждениях, то рекомендую книгу S. Klymchuk, S. Staples, «Paradoxes and Sophisms in Calculus».
Автор: mkot
