Бывает, когда требуется что-то замерить, я прибегаю к простому методу, который не слишком быстр, не слишком точен, не рекомендуется ни в одном официальном стандарте — но, всё-таки, ни разу меня не подводил. Опишу его здесь, хотя, даже просто называя его «методом», я уже немного его приукрашиваю. Пожалуйста, не пользуйтесь им, если нужно повесить шкафчики на кухне или вообще что угодно, на что вам придётся ежедневно глядеть в течение ближайших десяти лет. Из измерительных инструментов нам понадобится только лист формата A4 — и всё.
Рубрика «математика»
Лист формата А4 — мерило всех вещей
2026-01-11 в 20:30, admin, рубрики: бумага, математика, соотношение сторон, юморЕсли ИИ не мыслит, то как он решает математические задачи?
2026-01-07 в 12:48, admin, рубрики: AI, ИИ, математика, нейросетиСамый частый вопрос к тезису о том, что языковые модели не думают - чисто практический.
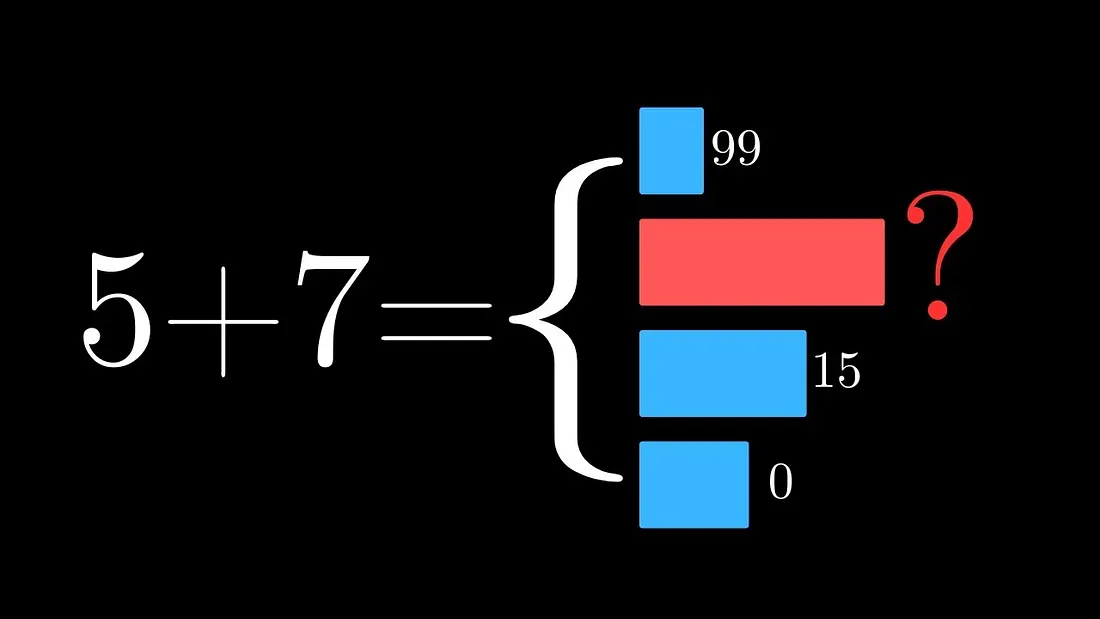
Возражение, которое я слышу чаще всего
Топовые фишки в LaTeX часть 1-4
2026-01-07 в 7:01, admin, рубрики: Latex book, latex шаблон, книга, математика, обучение, школаМеня зовут Виталий и я пишу уже который год самую большую книгу по математике для 4– 11 классов, а так же автор поста (рекомендую почитать) о ней. Пишу я ее в LaTeX и считаю, что современный учебник не должен быть черно-белым, а так же должен быть удобен для использования и учеником и учителем. Здесь я собрал базовые фишки, которые я использую (что-то чаще, что-то реже). Надеюсь, вы найдете что-нибудь полезное для себя:)
Фрактал, который провисел на моей стене 12 лет
2025-12-28 в 9:01, admin, рубрики: ruvds_перевод, графика, дизайн, математика, фракталы
Когда я учился в средней школе, то часто вместо того, чтобы заниматься делом, рисовал всякую всячину. Тогда же я умудрился изящно изрисовать чертёжный лист, комбинируя и повторяя множество квадратов — получилось что-то среднее между Читать полностью »
Как работают календарные системы
2025-12-24 в 14:07, admin, рубрики: python, время, история, Календарь, математикаНе для кого не секрет, что мы сейчас пользуемся григорианским календарём введённым после Октябрьской революции большевиками, но празднуем христианские праздники по юлианскому календарю, который отличается от григорианского на 13 дней. Но почему так происходит? Давайте разбираться.
Теория групп для всех: пульт для управления реальностью прямо из палаты
2025-12-23 в 11:51, admin, рубрики: визуализация, математика, перестановки, симметрия, теория группПочему теория групп порой кажется сложной и непонятной
Представьте себе, что вы открываете учебник по математике. На первой же странице видите:
«Гру́ппа — множество, на котором определена ассоциативная бинарная операция, причём »
В этот момент у вас сразу же появляются вопросы:
-
Откуда взялось это множество и зачем оно нужно?
-
Какая операция и что это вообще всё значит?
-
Почему я должен верить в эти аксиомы?
Подсчёт недостающих оценок для получения определённого итогового балла
2025-12-17 в 16:40, admin, рубрики: анализ данных, математика, оценки, школаЭтот материал для родителей, студентов и школьников, которые хотят при помощи математики оценить набор необходимых усилий, чтобы достичь определенных результатов.
У нас есть промежуточный набор оценок, и мы хотим посчитать, сколько нам надо получить четверок и пятерок, чтобы подойти к концу четверти/семестра с определенным баллом.
Введем условные обозначения:
-
Целевой балл t (target)
-
Текущая оценка (средний балл) m (mark)
-
Глубина d (deep) - количество оценок к данному моменту
Релятивизм виртуальной Вселенной
2025-12-11 в 11:23, admin, рубрики: математика, наука, Научно-популярное, релятивистская кинематика, физика, эйнштейнПредыдущие статьи: "Геометрическая головоломка на выходные", "Электродинамика виртуальной Вселенной", "Механика виртуальной Вселенной", "Квантовая механика виртуальной Вселенной (часть I), (часть II)
Квантовая механика виртуальной Вселенной (Часть II)
2025-12-09 в 14:37, admin, рубрики: квантовая механика, квантовая физика, математика, физикаЗдравствуйте, дорогие читатели.
В первой части мы начали разбирать квантовую механику виртуальной Вселенной. (Предысторию вы можете найти в предыдущих статьях цикла: «Геометрическая головоломка на выходные», «Электродинамика виртуальной Вселенной» и «Механика виртуальной Вселенной»).
Читать полностью »
Тёмная сторона Си: трюки, хаки, магия и алгоритмы
2025-12-09 в 8:05, admin, рубрики: C, timeweb_статьи, Алгоритмы, ГПСЧ, магия, математика, трюки, фаны, хакиДоброго времени суток, господа и дамы! Иногда у некоторых людей возникает желание заняться откровенным непотребством в программировании — то, что не несет практической пользы напрямую, но помогает развлечься. И я — не исключение. В этой статье я хочу рассказать вам о лайфхаках, трюках (магических и не очень), алгоритмах на языке C!
