В части 2 мы закончили с определениями всех формальных терминов и символов, которые вы можете увидеть в вопросе на StackOverflow об алгоритме Хиндли-Милнера. Так что теперь мы готовы перевести, о чём же там спрашивается, а именно — правила вывода утверждений о выводе типов. Приступим!
Читать полностью »
Рубрика «математика» - 193
Итак, вы всё ещё не понимаете Хиндли-Милнера? Часть 3
2013-08-15 в 8:01, admin, рубрики: hindley-milner, вывод типов, математика, модель Хиндли-Милнера, переводы, ПрограммированиеИтак, вы всё ещё не понимаете Хиндли-Милнера? Часть 2
2013-08-15 в 8:00, admin, рубрики: hindley-milner, вывод типов, математика, модель Хиндли-Милнера, переводы, Программирование В части 1 мы говорили о том, какие строительные блоки нужны для формализации Хиндли-Милнера, а в этом посте мы конкретизируем их определения и сформулируем формализацию в целом:
Читать полностью »
Наглядно о том, почему я не беру кредиты
2013-08-14 в 12:40, admin, рубрики: вклады, ипотека, кредиты, математика, Финансы для всех, метки: вклады, ипотека, кредиты, математика  Кредит — это когда банк вас грабит и вы ему за это ещё платите.
Кредит — это когда банк вас грабит и вы ему за это ещё платите.
Пожарный Сидоров бездействовал: банк горел — кредит гасился.
Привет!
Многие из вас, наверняка, слышали не раз подобные шутки про кредиты и ипотеку. Некоторые, наверное, не раз пользовались калькуляторами вкладов и кредитов, и оценивали выгодность того или иного способа накопления денег. Я тоже недавно заинтересовался этой темой, и подошёл к этой проблеме математически.
Читать полностью »
Эльзевир – мой вклад в его падение
2013-08-14 в 9:22, admin, рубрики: авторское право, копирайт, математика, наука, научные журналы, научные статьи, переводы, метки: авторское право, наука, научные журналы, научные статьиот переводчика: В свете недавно появившейся на Хабре публикации «Наука под замком», хотелось бы привести взгляд изнутри на проблему доступности научных публикаций британского математика из Кембриджского университета, пишущего в интернете по ником gowers.
P.S. Международные названия журналов, насколько мне известно, не имеют официальных переводов, поэтому перевод дан по смыслу с указанием оригинального названия

Нидерландская издательская компания Эльзевир (Elsevier) публикует множество самых известных мировых журналов по математике, включая «Успехи математики» («Advances in Mathematics»), «Доклады по математике» («Comptes Rendus Mathematique»), «Дискретная математика» («Discrete Mathematics»), «Европейский журнал по комбинаторике» («The European Journal of Combinatorics»), «История математики» («Historia Mathematica»), «Журнал по алгебре» («Journal of Algebra»), «Журнал теории приближений» («Journal of Approximation Theory»), «Журнал по комбинаторике. Серия А» («Journal of Combinatorics Series A»), «Журнал функционального анализа» («Journal of Functional Analysis»), «Журнал по геометрии и физике» («Journal of Geometry and Physics»), «Журнал математического анализа и его приложений» («Journal of Mathematical Analysis and Applications»), «Журнал по теории чисел» («Journal of Number Theory»), «Топология» («Topology»), «Топология и её приложения» («Topology and its Applications»). В течение многих лет компания подвергается жесткой критике за свою практику ведения бизнеса. Позвольте мне кратко обобщить основные пункты, на которых основана эта критика.
- Цены издательства непомерно высоки – настолько выше среднего, что просто удивительно, что это так долго сходит издательству с рук.
- Один из способов, с помощью которого им удается этого добиваться, – это так называемая «продажа пачкой», суть которой в том, что библиотеки не могут выбирать, на какие именно журналы подписаться, они могут выбрать либо большую подборку (сделанную издательством, а не библиотекой) либо вообще ничего. То есть если некоторые из журналов в «пачке» незаменимы для библиотеки, то ей приходится подписываться и по очень высоким ценам на большое число журналов по разным наукам; при этом многие из этих журналов библиотеке вообще не нужны («Журнал хаоса, солитонов и фракталов» являет собой яркий пример периодического издания, которое многие математики считают просто ничтожным, при этом библиотеки по всему миру вынуждены на него подписываться). Учитывая то, что бюджет библиотек часто весьма ограничен, на практике это означает, что из-за этого им просто не хватает средств, чтобы подписаться на многие журналы других издателей, которые гораздо нужнее. В результате страдают не только библиотеки, но и другие издательства, что безусловно, является одной из причин, почему Эльзевир предпочитает эту схему.
- Если библиотеки пытаются договориться о лучших условиях, Эльзевир просто отрезает им доступ ко всем своим журналам.
- Эльзевир поддерживает многие меры, такие как «Закон о научных работах» ( «Research Works Act» ), которые препятствуют попаданию работ в открытый доступ. Также издательство Эльзевир поддерживало законопроекты SOPA и PIPA и активно их лоббировало.
Я мог бы продолжить, но на этом остановлюсь.
Кажется необъяснимым, почему ситуация продолжает развивается подобным образом. В конце концов, математики (как и другие ученые) жалуются на это уже долгое время. Почему бы им просто не отказаться публиковаться в журналах, издаваемых Эльзевиром?
Представление чисел суммой двух квадратов и эллиптические кривые
2013-08-10 в 17:24, admin, рубрики: криптография, математика, эллиптические кривые, метки: эллиптические кривыеПусть p — нечётное простое число. Довольно широко известно, что p представимо в виде суммы двух квадратов целых чисел p=a2+b2 тогда и только тогда, когда p при делении на 4 даёт остаток 1: 5=12+22, 13=32+22, 17=12+42, ...; 3, 7, 11,… непредставимы. Куда менее известно, что a и b можно записать красивой формулой, имеющей непосредственное отношение к одной эллиптической кривой. Об этом результате 1907 года за авторством немца по фамилии Jacobsthal и о связанных вещах мы сегодня и поговорим.
Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a2+b2: квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).
Об одной изящной конструкции
2013-08-04 в 20:00, admin, рубрики: Алгоритмы, деревья, математика, структуры данных, метки: Алгоритмы, деревья, структуры данныхВведение
Начну статью с того, что расскажу, как я познакомился с этой изящной конструкцией. Занимаясь олимпиадным программированием, мы с моим преподавателем решали много интересных задач. И вот однажды мне попалась следующая задача:
Распечатать в порядке возрастания все несократимые дроби, знаменатель которых не превосходит n, n<=100.
Прочитав условие задачи до конца, она не показалась мне сложной (она таковой и не является). Первое, что пришло мне в голову это просто перебрать все знаменатели от 2 до n и для каждого знаменателя перебрать числители от 1 до знаменателя, при условии, что числитель и знаменатель взаимно просты. Ну, а за тем отсортировать их по возрастанию.
Такое решение верно и задача прошла все назначенные ей тесты. Однако, мой преподаватель сказал, что задачу можно решить намного красивее (он уже сталкивался с этой конструкцией). Так я и познакомился с этой замечательной конструкцией — деревом Штерна-Броко.
Читать полностью »
Вероятностные модели: борьба с циклами и вариационные приближения
2013-08-02 в 16:03, admin, рубрики: data mining, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, теория вероятностейВ четвёртой серии цикла о графических вероятностных моделях (часть 1, часть 2, часть 3) мы продолжим разговор о том, как справляться со сложными фактор-графами. В прошлый раз мы изучили алгоритм передачи сообщений, который, правда, работает только в тех случаях, когда фактор-граф представляет собой дерево, и в каждом узле можно без проблем пересчитать распределения грубой силой. Что делать в по-настоящему интересных случаях, когда в графе есть большие содержательные циклы, мы начнём обсуждать сегодня – поговорим о паре относительно простых методов и обсудим очень мощный, но непростой в использовании инструмент – вариационные приближения.
«Краник», или алгоритм для поиска цифр числа Пи
2013-08-02 в 14:45, admin, рубрики: Алгоритмы, математика, метки: Алгоритмы, математикаПривет! Недавно столкнулся с задачей подсчёта числа Пи до знака, номер которого будет выбирать пользователь. Сразу полез на Википедию, почитать, что за зверь такой, это Пи, и как его находить с заданной точностью. Формул, описывающих число Пи, уйма. Но для решения моей задачи всё в этих формулах упирается либо в точность и длину базовых типов языка (я выбрал Java), либо (для решения предыдущей проблемы) в длинную арифметику, которую мне реализовывать не очень-то хотелось. Читать полностью »
Распознавание рукописного ввода
2013-07-30 в 15:42, admin, рубрики: c++, Алгоритмы, математика, Программирование, С++, метки: Алгоритмы, математика, Программирование, С++Введение
В данной статье пойдет речь о методе распознавания рукописного ввода путем математического анализа всех точек плоскости и перебора всех возможных комбинаций с целью отыскать наиболее лучшее наложение контрольных точек на ранее описанные фигуры. Поясню.
Рукописный ввод — это рисование мыслимым «пером» определенной фигуры. Рисование в компьютерных системах — это сохранение в графической памяти информации обо всех пикселях графического контекста. «Точка на плоскости» в математике — понятие абстрактное. В компьютерной же графике за этим понятием скрывается «пиксель». Данный алгоритм распознавания будет анализировать предоставленный ему набор точек( пикселей ) и пытаться в нем отыскать наиболее возможную и похожую фигуру. Фигура, в свою очередь, это каркас, содержащий лишь основные( контрольные ) точки, делающие фигуру уникальной.
Матчасть
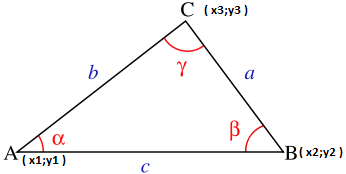
Вообще говоря, сердце алгоритма — всем известная со времен школы Теорема Косинусов, являющаяся обобщенной теоремой Пифагора. Зная координаты трех точек плоскости и их порядок «появления» на ней, мы можем с легкостью определить угол, описанный этими точками( Вершина угла — вторая по счету точка ):
A( x1;y1 )
B( x2;y2 )
C( x3;y3 )расстояния между точками находятся по теореме Пифагора
a^ = b^ + c^ — 2*b*c*cos(ALPHA)
cos(BETA) = (b^+c^-a^) / 2*b*c
Зная косинус, величину угла легко можно вычислить.
Среди набора точек, которые подаются на вход алгоритма, необходимо «подставить» точки во всевозможные каркасы фигур( о них выше ) и выбрать наилучшее решение среди найденных. Делается это следующим образом:
- Мы берем первую и последнюю точки каркасов фигур. Уже две есть, осталось отыскать третью ( для нахождения величины угла ).
- Поиск третьей осуществляется перебором все последующих точек после первой. Решение включать точку в предполагаемый каркас фигуры принимается на основе двух анализов:
- Попытка подставить точку в угол( в качестве третьей, заключительной ) и проверить его на соответствие величине того же угла в каркасе реальной фигуры.
- Проверить отношение сторон получившегося угла с тем же отношением сторон угла в каркасе реальной фигуры.
Если эти два условия выполняются, то алгоритм принимает решение о включении точки из набора точек в мыслимый каркас( при этом увеличиваем величину похожести на текущую анализируемую фигуру ).
Если, допустим, у нас есть несколько анализируемых каркасов, например, «8» и «6». И результат алгоритма распознавания: «8»-80%, «6» — 90%, то решение принимается в пользу той фигуры, в каркасе которой присутствует больше контрольных точек, т.е в пользу восьмерки.
Процент сходства набора точек с точками в каркасе высчитывается просто: суммируются все точки, которые сошлись с теми же точками в каркасе и находится отношение. Допустим, если в каркасе N контрольных точек, а у нас сошлось M, то процент сходства —
M / N * 100
Apache Mahout. Метрики для определения схожести пользователей
2013-07-30 в 14:29, admin, рубрики: big data, Алгоритмы, математика, метки: Алгоритмы Привет.
Читаю книгу Mahout in Action. Столкнулся с эффектом “смотрю в книгу – вижу фигу”. Для его устранения решил конспектировать.
Apache Mahout – это библиотека для работы с алгоритмами машинного обучения, которая может быть использована как надстройка к Hadoop или самостоятельно. В библиотеке реализованы методы коллаборативной фильтрации, кластеризации и классификации.
Рассматриваем рекомендательную систему на основе коллаборатвной фильтрации. Она может быть пользователе-ориентированной (user-based) или свойство-ориентированной (item-based).
Коллаборативная фильтрация — это один из методов построения прогнозов, использующий известные предпочтения (оценки) группы пользователей для прогнозирования неизвестных предпочтений другого пользователя. Его основное допущение состоит в следующем: те, кто одинаково оценивали какие-либо предметы в прошлом, склонны давать похожие оценки другим предметам и в будущем. (из википедии)
Одно из основных понятий пользователе-ориентированных рекомендательных систем это метрика для определения схожести пользователей. Предположим что мы имеем данные по просмотрам и оценкам фильмов разными пользователями. Будем сравнивать двух пользователей: X и Y. Они выставили оценки фильмам X(x1, x2, ..., xn) и Y(y1, y2, ..., ym), где n, m – количество оценок поставленных первым и вторым пользователем соответственно. N – количество оценок, которые были поставленны обоими пользователями одним и тем же фильмам (пересечение множеств фильмов посмотренных первым и вторым). Будем считать что (xi, yi) – это пара оценок выставленная пользователями одному фильму.
В Mahout реализованы метрики на основании нескольких алгоритмов. Описываю сами алгоритмы, а не их реализации в Mahout.