В этой статье будет описано, как один чересчур поверивший в себя программист пытался взломать один из фундаментальных алгоритмов криптографии. Эта статья признана огородить других от подобных попыток, или наоборот, заинтересовать новых смельчаков для подобной авантюры. Сначала я опишу суть алгоритма на простом коде, затем перечислю методы и идеи, которыми я пытался его взломать.
Рубрика «эллиптические кривые»
Как я НЕ взломал ED25519
2025-08-22 в 7:25, admin, рубрики: Curve25519, Ed25519, edwards curve, python, криптография, математика, уязвимости, хакинг, эллиптические кривыеТайное уравнение, позволявшее США следить за всеми
2025-06-20 в 9:02, admin, рубрики: mitm, NIST, SSL, шифрование, эллиптические кривые1.0 Введение
В 2006 году АНБ скрыла в криптографическом стандарте Dual EC DRBG математический бэкдор. Агентство отрицало его наличие восемь лет. Затем утечки Сноудена подтвердили его существование.
Двойные эллиптические кривые (Dual Elliptic Curve) используются как безопасные генераторы случайных чисел (RNG). Математический бэкдор позволял правительству США расшифровывать SSL-трафик Интернета (Green 2013)1.
Эта статья будет технически глубоким исследованием для программистов. Мы реализуем и исходную правительственную научную статью (SP 800-90 2006)2Читать полностью »
Сложение точек эллиптической кривой в числах, как на калькуляторе
2025-05-25 в 15:04, admin, рубрики: ECDH, ecdsa, Алгоритмы, криптография, математика, умножение, эллиптические кривыеПрактика показывает, что многие лучше понимают математические концепции криптографии на максимально конкретных примерах, приводимых в числах непосредственно. Цель данной статьи - выстроить таким способом некоторую «интуицию» для одной из базовых в современной криптографии операций - сложения точек эллиптической кривой. Мы посмотрим, что за арифметика стоит за алгоритмическими, компьютерными реализациями этой операции.
Задача с эмодзи
2025-05-21 в 13:38, admin, рубрики: elliptic curves, виет, математические задачи, эллиптические кривыеСложность текста: 2-3/5
Необходимые знания: должно быть достаточно основ теории многочленов, например, формул Виета
На случай, если современная культура окажется утерянной во времени, дам немного контекста, чтобы вы понимали, почему эта задача стоит изучения.
Интернет переполнен «математическими задачками с эмодзи», которые выглядят примерно так:
OpenSSH против SSH
2023-08-02 в 9:00, admin, рубрики: BIND, djbdns, DNS, Dropbear, ECC, ECDH, ecdsa, ECMQV, GSS-API, IT-стандарты, open source, openssh, rsa, ruvds_статьи, secure shell, ssh, SSH FTP, ssh-2, Suite B, алгоритм Диффи-Хеллмана, Блог компании RUVDS.com, Даниэль Бернштейн, информационная безопасность, протоколы, эллиптические кривые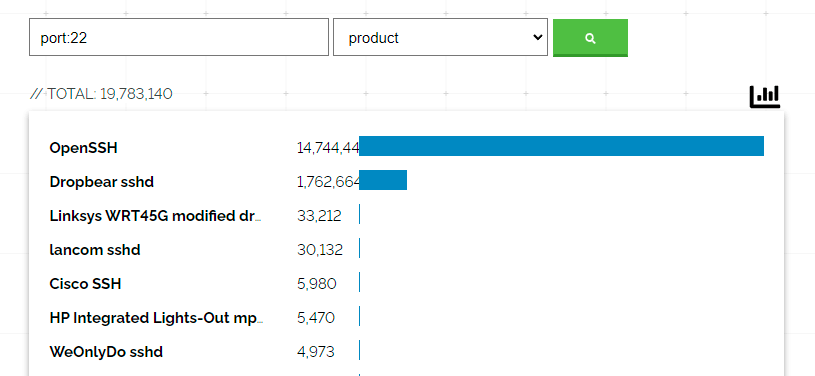
Рис. 1. Разные реализации SSH, источник: Shodan
Формально протокол SSH определён в ряде стандартов RFC (список ниже). В то же время есть много реализаций этого протокола. OpenSSH — самая популярная из них, хотя не единственная. Например, вот альтернативная реализация SSH на Go (и несколько примеров кастомных серверов на её основе). По статистике Shodan, вторым по популярности демоном SSH является Dropbear SSH (рис. 1). Все остальные далеко позади, если судить по количеству адресов на порту 22.
На практике спецификации OpenSSH содержат в себе все стандарты RFC для SSH, включая черновики, а также немножко сверх этого.Читать полностью »
Старая математика ломает постквантовые шифры
2023-01-29 в 13:30, admin, рубрики: NIST, SIKE, Блог компании GlobalSign, информационная безопасность, квантовая криптография, кривые второго порядка, криптография, математика, Научно-популярное, постквантовые шифры, теорема Кани, теорема ферма, факторизация, эллиптические кривые
Мир криптографии постепенно готовится к приходу квантовых вычислений, где вместо двоичной логики используются кубиты. Предполагается, что именно криптография станет одним из первых применений квантовых компьютеров.
Проблема в том, что современные алгоритмы вроде RSA и Диффи-Хеллмана (в том числе на эллиптических кривых) не способны противостоять квантовым атакам. Поэтому в июле 2022 года Национальный институт стандартов и технологий США (NIST) опубликовал набор алгоритмов шифрования, потенциально способных противостоять взлому на квантовых компьютерах — так называемые «постквантовые шифры».
Один из «постквантовых» шифров сразу взломали. Но самое интересное — метод, который применили исследователи.
Читать полностью »
Шифрование сертификатов TLS — как формируется цифровая подпись
2022-09-24 в 18:58, admin, рубрики: Curve25519, Curve448, Ed25519, Ed448, ErDSA, Frost & Sullivan, globalsign, IT-стандарты, RFC 8032, SHA-2, SHA-512, SHAKE256, SSL, TLS, TLS 1.3 RFC 8446, Блог компании GlobalSign, информационная безопасность, криптография, Разработка веб-сайтов, сертификаты, цифровая подпись, шифрование, эллиптические кривые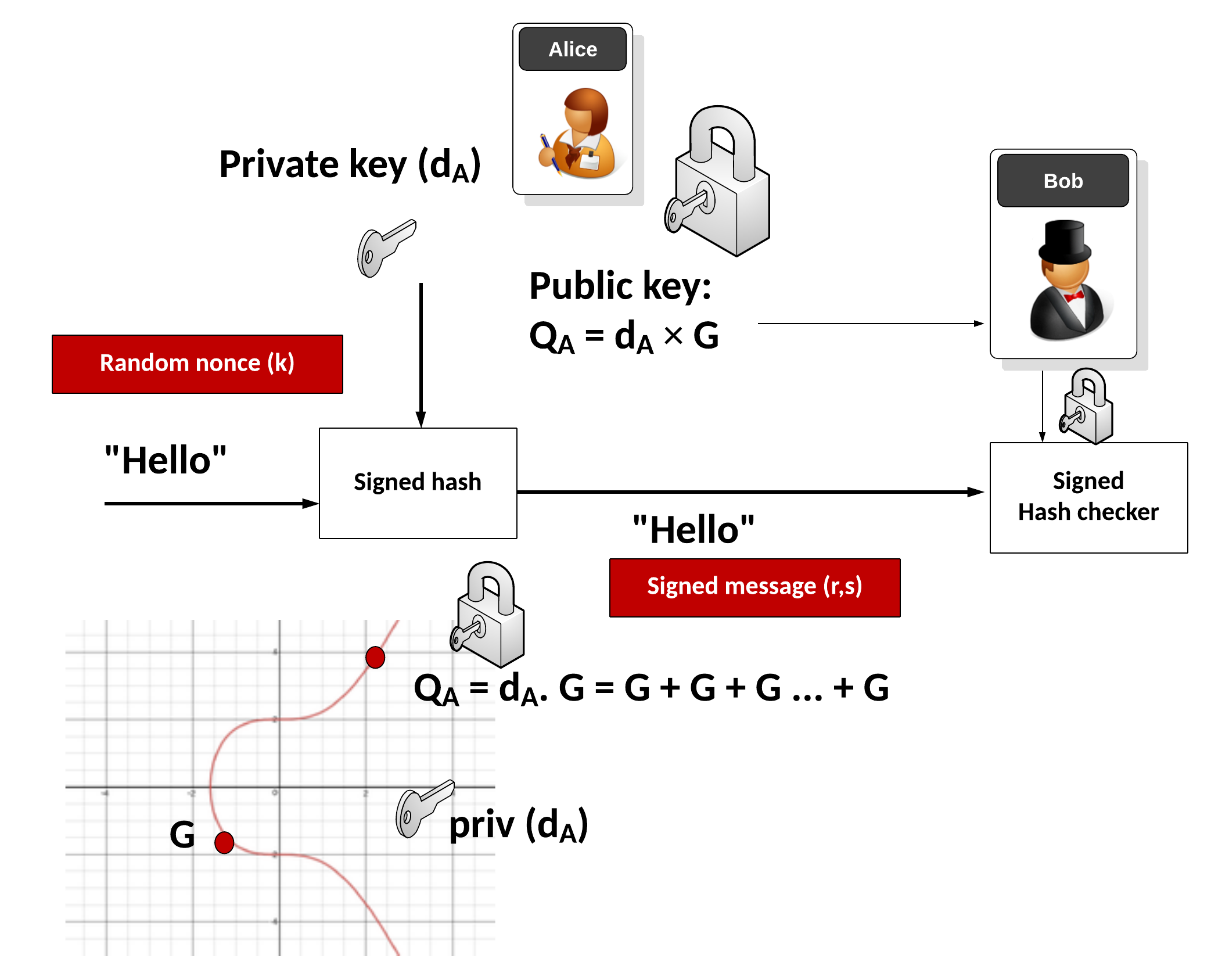
По оценке независимой исследовательской и консалтинговой компании Frost & Sullivan, TLS-сертификаты от GlobalSign обеспечивают максимально надёжное шифрование. В том числе за это GlobalSign получила в сентябре 2022 года награду 2022 Global Competitive Strategy Leadership Award.
Но возникает вопрос, чем же отличается шифрование в разных сертификатах? В частности, какие алгоритмы используются для криптографической подписи?
Читать полностью »
Reticulum — радиопротокол для mesh-сети. Зашифрованная пиринговая связь без интернета
2022-04-22 в 15:04, admin, рубрики: e2e, ECDH, lora, LXMF, Mesh-сети, Nomad Network, NYC Mesh, Reticulum, Sideband, анонимность, Блог компании GlobalSign, информационная безопасность, криптография, мессенджеры, радиосвязь, эллиптические кривые
Как мы обсуждали ранее, отключение интернета в конкретной стране или городе — не вымышленная угроза, а вполне реализуемое действие. В частности, международная ассоциация Internet Society зафиксировала в 2021 году 49 искусственно вызванных шатдаунов.
Но есть эффективные технологии, которые позволят пережить возможный шатдаун. Например, mesh-сети для радиосвязи.
Читать полностью »
SageMath и CoCalc: как всё начиналось. Часть первая
2020-02-05 в 8:00, admin, рубрики: C, c++, cocalc, computer algebra, open source, sage, sagemath, алгебра, алгебраическая геометрия, Биографии гиков, высшая алгебра, гипотеза Бёрча - Свиннертон-Дайера, задачи тысячелетия, компьютерная алгебра, математика, математическое программирование, модулярные формы, теория чиел, Управление сообществом, эллиптические кривыеПубликуется с разрешения автора.
От переводчика
Текст, перевод которого я намерен представить вашему вниманию, — краткая автобиография (называющаяся в оригинале «Mathematical Software and Me: A Very Personal Recollection», то есть «Математическое ПО и я: очень личные размышления»), написанная в 2009-м году Уильямом Стайном (имя которого по-русски иногда пишут как «Вильям Стейн»), бывшим профессором математики Вашингтонского Универститета, получившим степень Ph. D. в Беркли (Калифорния). Математическая составляющая профессиональных интересов доктора Стайна — теория чисел. Этот текст о его, возможно, главном деле — системе компьютерной математики, ранее называвшейся Sage, в настоящее время переименованной в SageMath, существующей также в облачной версии, которая раньше называлась SageMathCloud, а теперь — CoCalc. (На Хабре эти системы неоднократно упоминались: например, freetonik написал о Sage, а sindzicat поведал о SageMathCloud.) Когда я прочитал «Mathematical Sofrware and Me» первый раз, этот текст меня очень впечатлил. И прежде, чем перейти к самому переводу, я попробую кратко объяснить, чем же именно.

Автор оригинального текста (слева)
Читать полностью »

