Вступление
Вижу, что на Хабре люди серьёзные собрались. Статью про трёхмерие на счёт «раз» разобрали. Однако пространствами постоянной кривизны никого не удивишь в наше время. Тем не менее всегда находятся желающие заглянуть выше, в четырёхмерие. Ну что ж, именно с такими любознательными коллегами мы продолжаем разговор и переходим на следующий уровень по размерности.
Моя задача не просто рассказать про разбиения пространств постоянной кривизны любой размерности на правильные многогранники, а сделать это так, чтобы материал поняли даже вчерашние школьники, окончившие 11 классов. Я люблю статьи на Хабре именно за их доходчивость, понятность, простоту, не смотря на сложность материала, и в таком же качестве стараюсь подавать сведения в публикациях. В ВУЗах и в отечественных публикациях предлагаемый материал возможно рассматривается, но, как мне кажется, не в таком виде. Думаю, что информация будет полезна и для студентов. В иностранной литературе данный материал есть, соответственно не на русском языке, в сильно сжатом виде и с использованием высшей математики. Тут я всё «разжёвываю» для школьников, без высшей математики, фактически на одной геометрической интуиции. Мы увидим в следующей статье, как будет сделан переход от 4D к 5D с помощью геометрии, наглядно, без высшей алгебры. Это будет самый сложный шаг, но кто его поймёт, тот поймёт и все остальные размерности от 6 и выше. Не уверен, что мне удалось всё основательно «разжевать», поэтому, если будут дополнительные вопросы — задавайте, это поможет мне улучшить статью.
В данной публикации идея выкладок полностью та же, что и в предыдущей статье, только на одну размерность выше , так что, если кто-то ещё не успел с ней ознакомиться, желательно это сделать, чтобы понимать, что происходит.
Сначала ещё раз дадим все определения, только уже для 4-мерных многогранников и соответствующего символа Шлефли. Не хочется сразу давать общие формулировки, чтобы не запутать не подготовленных читателей, которые с данным предметом, возможно, имеют дело впервые. Затем дадим постановку задачи. В данной публикации, похоже, что она приняла более строгий и стройный вид. Если ошибусь в каких-то деталях, то ничего страшного, это ведь не бумажная публикация, подредактирую и поправлю, чтобы всё было красиво. Основные выкладки и результат правильные, за это не переживайте, потом даже ссылки на авторитетных авторов дам, если что. Заглянув к этим авторам вы поймёте, что мой труд, в виде этих нескольких публикаций, не напрасный.
Определения. Аксиомы. Постановка задачи
В многогранниках много разных углов, двугранным углом мы называем двугранный смежный угол, между смежными гранями, т.е. гранями имеющими общее ребро.
Определение правильного многогранника даю рекурентное и своими словами, ведь Хабр — не место для копипастеров.
Правильным 4-мерным многогранником называется выпуклый многогранник, у которого все 3-мерные грани являются правильными многограниками, равными между собой и все углы между 3-мерными гранями равны между собой.
Есть утверждение, что разбиению (n-1)-мерной сферы взаимно однозначно соответствует правильный n-мерный многогранник, при n>1. То есть размерность многогранника на одну выше, чем размерность сферы, которую разбиваем. Например, если вершины разбиения 3-мерной сферы соединить рёбрами, соответствующими дугам разбиения, то получится 4-мерный многогранник. Не знаю как это утверждение доказывается и доказывается ли вообще. Поэтому оно принимается за аксиому и считаем его верным во всех размерностях пространств. Для двумерной сферы на примере икосаэдра это было показано в видео ролике в предыдущей публикации. Можно сказать, что в трёхмерии (т.е. для разбиения двумерной сферы) этот факт установлен экспериментально, а в четырёхмерии и выше, считаем, что всё аналогично. Вроде бы тут всё чисто, интуитивно понятно, что так оно и есть.
Определение символа Шлефли тоже даю своими словами.
Символом Шлефли называется последовательность чисел {p1, p2, p3} задающая алгоритм построения правильного многогранника следующим образом:
— взять правильные {p1} угольники, объединить их по рёбрам, так, чтобы в каждой вершине сошлось по p2 штук таких {p1}, получим {{p1}, p2} или коротко {p1, p2}
— взять, полученные на предыдущем шаге, {p1, p2} и объединить их по плоским граням так, чтобы в каждом ребре сошлось p3 штук таких {p1, p2} трёхмерных многогранника.
Уже напрашивается индукция в определении, не правда ли? Общее определение, для n-мерного правильного многогранника дам в следующей публикации. Пока лучше рассмотреть частный случай, чтобы проще было понять и не отвлекаться на общие формулировки.
И ещё одна мысль (постановка задачи), которая, выраженная в грубой форме, влоб, оказывается не верна, но она не используется при выкладках, поэтому никак не влияет на результат, но за то она является движущей силой исследований :) Мысль заключается в том, что для любого символа Шлефли в любой размерности Существует правильный многогранник, который разбивает одно из пространств постоянной кривизны соответствующей размерности. Мы видели, что при разбиении двумерных пространств эта мысль верна, там любой символ Шлефли что-нибудь да разбивал. Слово «Существует» выделено большой буквой, так как на самом деле это не верно для размерностей 4 и выше. Допускать существование всегда — это конечно вольности, но можно сформулировать постановку задачи таким образом, что эта мысль окажется законной, а именно:
количество различных значений символа Шлефли счётное множество, разбить это множество на не пересекающиеся подмножества (классы) конечные или бесконечные по типам:
— класс символов задающих разбиение Сферического пространства на правильные многогранники соответствующей размерности;
— ---//--- разбиение Евклидова пространства ---//---
— ---//--- разбиение пространства Лобачевского на правильные многогранники Конечного объёма ---//---
— ---//--- разбиение пространства Лобачевского на правильные предельные многогранники конечного объёма ---//--- (такие, у которых вершины попадают прямо на абсолют — границу диска Пуанкаре)
— ---//--- разбиение пространства Лобачевского на правильные многогранники бесконечного объёма ---//--- (если получающиеся фигуры условно считать правильными многогранниками)
— класс «плохих» символов, которым невозможно поставить в соответствие какой-то многогранник или какое-то разбиение пространства постоянной кривизны.
При перечислении этих классов мы забежали немного вперёд, и в разбиениях пространств Лобачевского, выше, выделили три подмножества (класса), вместо одного, как для Сферы и Евклида.
Иными словами, наша задача заключается в исследовании всех возможных значений символа Шлефли во всех размерностях, во всех трёх пространствах постоянной кривизны. Это мотивация, цель и задача. В данной публикации размерность разбиваемых пространств постоянной кривизны = 3, размерность получаемых при этом многогранников = 4.
Замысел решения задачи
Сама идея решения проста, как и в предыдущей статье о трёхмерии, нужно с одной стороны по параметрам символа Шлефли {p1, p2} вычислить двугранный угол (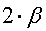 ) многогранника и сравнить этот угол с
) многогранника и сравнить этот угол с 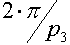 т.е. чтобы полный оборот (
т.е. чтобы полный оборот (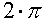 ) вмещал целое число многогранников, сошедшихся в ребре. Здесь p3 — третий параметр символа Шлефли {p1, p2, p3}, задающего разбиение 4-мерного пространства на многогранники {p1, p2}, означающий количество многогранников {p1, p2}, сошедшихся в ребре.
) вмещал целое число многогранников, сошедшихся в ребре. Здесь p3 — третий параметр символа Шлефли {p1, p2, p3}, задающего разбиение 4-мерного пространства на многогранники {p1, p2}, означающий количество многогранников {p1, p2}, сошедшихся в ребре.
1. Если окажется, что 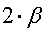 =
= 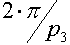 то значит искривлять пространство не надо, всё и так сошлось красиво, т.е. это Евклидово пространство. Как видите, двойка напрашивается сократиться, поэтому в расчётах фигурирует не сам двугранный угол многогранника
то значит искривлять пространство не надо, всё и так сошлось красиво, т.е. это Евклидово пространство. Как видите, двойка напрашивается сократиться, поэтому в расчётах фигурирует не сам двугранный угол многогранника 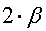 а его половина =
а его половина = 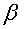
2. Если окажется, что 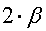 <
< 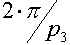 т.е. двугранный угол маленький, то многогранник, вместе с его углами, нужно «раздуть», чтобы углы увеличились до нужных значений, значит нужно поместить его на трёхмерную сферу, т.е. это сферический случай.
т.е. двугранный угол маленький, то многогранник, вместе с его углами, нужно «раздуть», чтобы углы увеличились до нужных значений, значит нужно поместить его на трёхмерную сферу, т.е. это сферический случай.
3. Если окажется, что 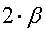 >
> 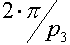 т.е. двугранный угол большой, то многогранник, вместе с его углами, нужно «сдуть», чтобы углы уменьшились до нужных значений, значит нужно поместить его в трёхмерное пространство Лобачевского, т.е. это гиперболический случай.
т.е. двугранный угол большой, то многогранник, вместе с его углами, нужно «сдуть», чтобы углы уменьшились до нужных значений, значит нужно поместить его в трёхмерное пространство Лобачевского, т.е. это гиперболический случай.
Про то, что значит «раздуть» и «сдуть» многогранник (многоугольник) было рассказано в предыдущей статье, где мы видели, что сумма углов треугольника (многоугольника) увеличивается, когда помещаем его на сферу, треугольник как бы раздувается и, что сумма углов треугольника уменьшается, когда помещаем его в гиперболическое пространство, треугольник как бы сдувается. Там мы это видели в двумерии, всё аналогично происходит с углами в 3-мерных пространствах и в пространствах высших размерностей.
Однако если углы правильных многоугольников мы знаем наизусть, то двугранные углы трёхмерных правильных многогранников уже запомнить наизусть сложнее, хотя, конечно, все эти углы известны. Мы увидим в следующей публикации, когда будем забираться в пятимерное пространство, что вывод формулы двугранного угла многогранника становится не тривиальной задачей и сама формула выходит на первый план. Можно было бы даже статью назвать: формула двугранного угла правильного, выпуклого многогранника в n-мерном Евклидовом пространстве. Но на самом деле эта формула является не только целью предлагаемых публикаций, но и средством, помогающим выявлять многогранники в пространствах высших размерностей. Т.е. все вопросы тут тесно связаны и интересны каждый из них по отдельности и все вместе взятые, поэтому выбрать лаконичное название для этих статей действительно проблематично.
Теперь остаётся только сделать выкладки для вычисления двугранного угла по параметрам символа Шлефли {p1, p2}, а сравнить полученные значения с 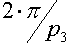 и выписать ответ, в виде таблицы, и школьник сможет. Впрочем, вычислить двугранный угол по параметрам p1, p2 тоже оказывается не сложно. Вот в следующей размерности, там посложнее, там уже появляется изюминка :) но об этом в следующей публикации.
и выписать ответ, в виде таблицы, и школьник сможет. Впрочем, вычислить двугранный угол по параметрам p1, p2 тоже оказывается не сложно. Вот в следующей размерности, там посложнее, там уже появляется изюминка :) но об этом в следующей публикации.
Вычисление двугранного угла у правильного многогранника {p1, p2}
Прошу прощения, в предыдущей статье забыл про вспомогательные углы сказать, которые нам понадобятся для расчётов. Это углы 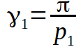 и
и 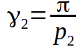 . Кто внимательно читал предыдущую статью, тот заметил, что там на чертеже угол
. Кто внимательно читал предыдущую статью, тот заметил, что там на чертеже угол 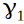 был обозначен, вычислен и получился
был обозначен, вычислен и получился 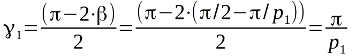 . Там мы измеряли угол правильного многоугольника в вершине C. Теперь взяв эту вершину и две соседние с ней вершины получим равнобедренный треугольник, вот
. Там мы измеряли угол правильного многоугольника в вершине C. Теперь взяв эту вершину и две соседние с ней вершины получим равнобедренный треугольник, вот 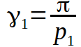 — это угол при основании этого треугольника, он теперь нам понадобится. Также для 3-хмерного многогранника нам понадобится угол
— это угол при основании этого треугольника, он теперь нам понадобится. Также для 3-хмерного многогранника нам понадобится угол 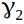 — это угол при основании равнобедренного треугольника, у правильного многоугольника {p2}, лежащего в основании равнобедренной пирамиды. Пирамида получается отсечением у {p1, p2} одной, изучаемой вершины, по плоскости близлежащих вершин. Обратите внимание на простой, но важный факт, что поскольку в вершине пирамиды сходится p2 штук правильных p1-угольников, то в основании этой пирамиды получается правильный p2-угольник. Этим мы и пользуемся, для вычисления угла
— это угол при основании равнобедренного треугольника, у правильного многоугольника {p2}, лежащего в основании равнобедренной пирамиды. Пирамида получается отсечением у {p1, p2} одной, изучаемой вершины, по плоскости близлежащих вершин. Обратите внимание на простой, но важный факт, что поскольку в вершине пирамиды сходится p2 штук правильных p1-угольников, то в основании этой пирамиды получается правильный p2-угольник. Этим мы и пользуемся, для вычисления угла 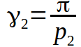
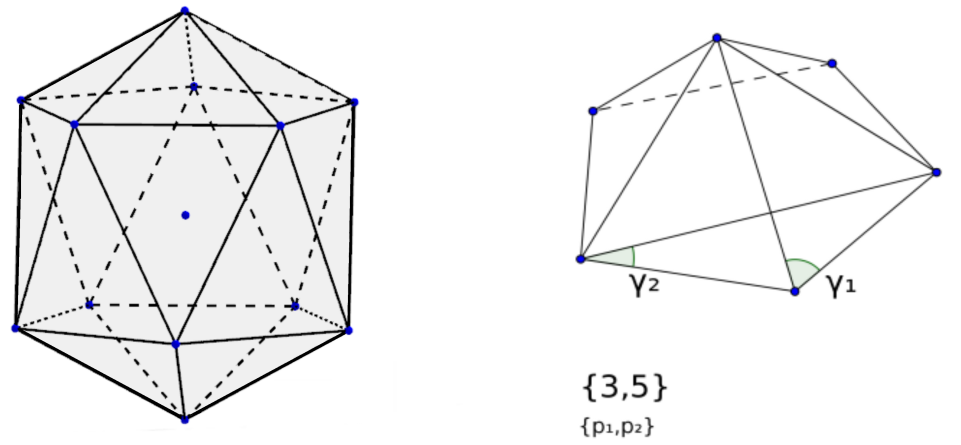
На рисунке рассмотрен пример с икосаэдром, тут 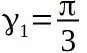 ,
,  в общем случае для произвольного {p1, p2}, получим
в общем случае для произвольного {p1, p2}, получим 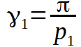 ,
, 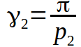 . Пока что мы находимся в Евклидовом пространстве, поэтому сумма углов треугольника по прежнему равна
. Пока что мы находимся в Евклидовом пространстве, поэтому сумма углов треугольника по прежнему равна 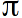 .
.
Теперь рассмотрим эту равнобедренную пирамидку поближе. Для вычисления двугранного угла достаточно рассмотреть не всю эту пирамиду, а только одно ребро и две грани, содержащие это ребро.
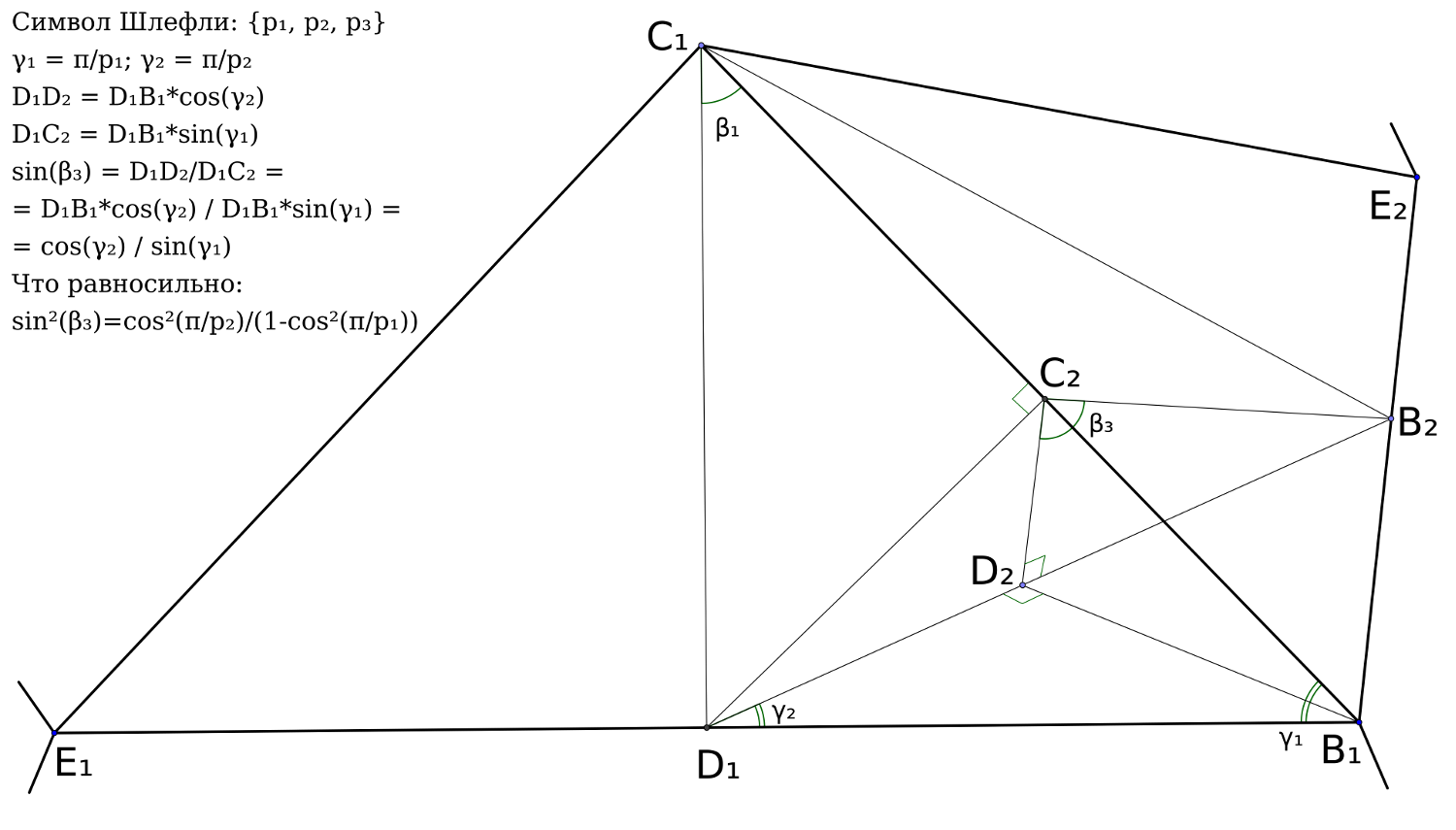
В общем случае для {p1, p2} рассмотрим ребро 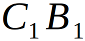 и найдём
и найдём 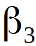 это и есть половина искомого нами угла, т.е. половина двугранного угла многогранника {p1, p2}. Дам пояснения о дополнительных построениях:
это и есть половина искомого нами угла, т.е. половина двугранного угла многогранника {p1, p2}. Дам пояснения о дополнительных построениях: 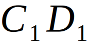 и
и 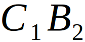 — высоты в соответствующих равнобедренных треугольниках. Плоскость равнобедренного треугольника
— высоты в соответствующих равнобедренных треугольниках. Плоскость равнобедренного треугольника 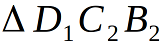 — ортогональна ребру
— ортогональна ребру 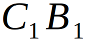 по построению, поэтому плоский угол
по построению, поэтому плоский угол 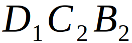 этого треугольника равен по величине искомому двугранному углу правильного многогранника {p1, p2}. Не сложные расчёты записаны левее чертежа, внимательно прочитайте их пожалуйста. Если вы знаете определение синуса и косинуса, то трудностей не должно возникнуть. Итак:
этого треугольника равен по величине искомому двугранному углу правильного многогранника {p1, p2}. Не сложные расчёты записаны левее чертежа, внимательно прочитайте их пожалуйста. Если вы знаете определение синуса и косинуса, то трудностей не должно возникнуть. Итак:
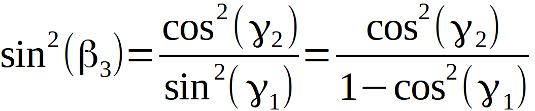
Можно, конечно, вычислить этот угол через фундаментальный тетраэдр (с вершинами в центре 3D-грани, центре 2D-грани, середине ребра и вершине многогранника), так классики и делают, но тогда переход по размерностям становится затруднительным, во всяком случае школьникам такое вряд ли удастся разъяснить. Поэтому предлагаемый в этой публикации подход, к вычислению двугранного угла, выбран сознательно. По меньшей мере, это ещё один способ, для вычисления этого угла. Кому-то понятнее один способ, кому-то другой.
Вычисления и сравнения углов
Как и говорили, сравниваем угол с 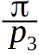 и записываем результаты сравнения в виде таблицы. Сравнения удобнее выполнять не для самих углов, а для синусов в квадрате этих углов, чтобы не загромождать записи арксинусами, ввиду того, что такая получилась формула для бетта.
и записываем результаты сравнения в виде таблицы. Сравнения удобнее выполнять не для самих углов, а для синусов в квадрате этих углов, чтобы не загромождать записи арксинусами, ввиду того, что такая получилась формула для бетта.
Суть сравнения в виде формулы:
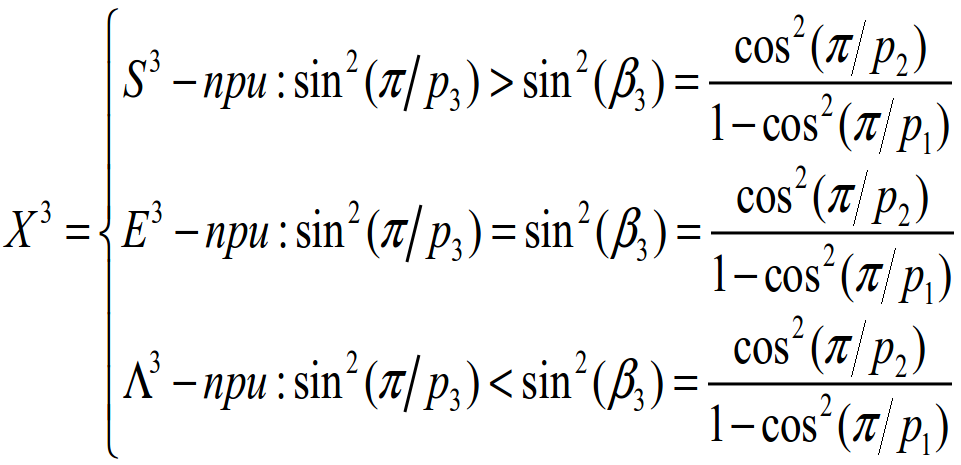
где X^3 — общее обозначение пространств постоянной кривизны, S^3 — трёхмерная сфера, E^3 — Евклидово трёхмерное пространство, Λ^3 — трёхмерное пространство Лобачевского.
Результат сравнения в виде таблицы:
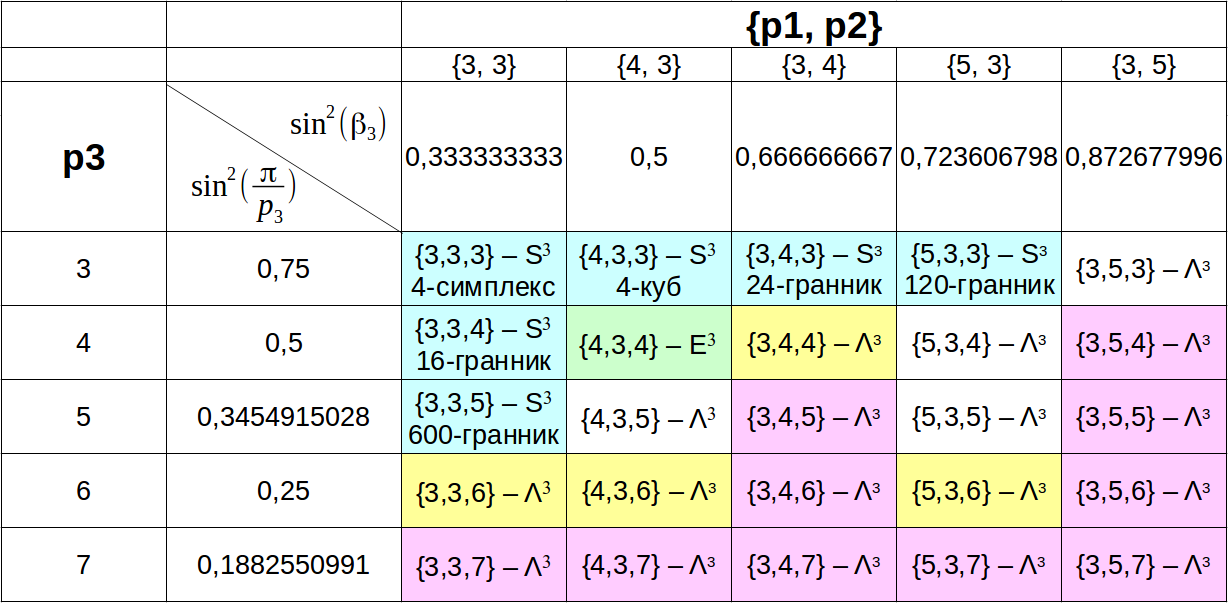
Где:

Ещё раз небольшие пояснения — сравниваются второй столбец, для 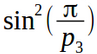 и третья строка, для
и третья строка, для 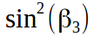 . Например:
. Например:
1. столбец {4,3} сравнивается со строкой p3=4, получаем 0.5 = 0.5 — значит {4,3,4} — разбивает Евклидово 3-мерное пространство, это привычные кубы, сходящиеся по 4 в ребре. :) Элементарно.
2. Для столбца {3,3} и строки p3=3 имеем 0.5<0.75 — значит {3,3,3} — разбивает 3-мерную сферу (и ему соответствует 4-мерный многогранник).
3. Для столбца {5,3} и строки p3=6 имеем 0.723>0.25 — значит {5,3,6} — разбивает 3-мерное пространство Лобачевского на правильный, предельный многогранник. Предельный можно понять по тому, что у него вершинная фигура {p2,p3} = {3,6} — разбивает двумерное пространство Евклида, т.е. плоскость Евклида.
В общем случае если {p1, p2, p3} — разбивает пространство Лобачевского, то дальше роль играет вершинная фигура:
— если {p2, p3} — разбивает Евклида, то {p1, p2, p3} — предельный многогранник,
— если {p2, p3} — разбивает сферу, то {p1, p2, p3} — имеет конечный объём и размеры,
— если {p2, p3} — разбивает плоскость Лобачевского, то {p1,p2,p3} — имеет бесконечный объём.
Это утверждение без доказательства, думаю, что оно верное и знаю почему, но строго и по простому доказать и показать не могу. Там включается орисфера, на поверхности которой Евклидова геометрия. А вершинная фигура, как раз отсекает орисферу для предельного многогранника.
Подведение итогов
Итак, мы научились вычислять двугранный угол правильного многогранника по его символу Шлефли {p1, p2}, на всякий случай выпишу ещё раз:
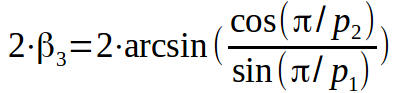
И нашли 6-ть разбиений трёхмерной сферы на правильные трёхмерные многогранники:
{3,3,3} — тетраэдры, сошедшиеся по 3 в ребре,
{4,3,3} — кубы, сошедшиеся по 3 в ребре,
{3,3,4} — тетраэдры, сошедшиеся по 4 в ребре,
{3,4,3} — октаэдры, сошедшиеся по 3 в ребре,
{5,3,3} — додекаэдры, сошедшиеся по 3 в ребре,
{3,3,5} — тетраэдры, сошедшиеся по 5 в ребре.
А значит и 6-ть соответствующих правильных 4-мерных многогранника с теми же символами Шлефли. Правда посчитать в общем виде количество вершин, рёбер, граней и гиперграней этих многогранников не так просто, как кажется на первый взгляд. В частных случаях для 4-тетраэдра, 4-куба, 4-октаэдра (ортаэдра) это можно сделать по индукции, но для остальных многогранников этот трюк не срабатывает.
К сожалению у меня нет своих картинок этих многогранников, поэтому отсылаю к википедии, там для четырёхмерия даны красивые картинки.
Так же, как когда мы смотрим на тетрадь в клеточку (разбиение {4, 4}) то видим структуру, как бы сама плоскость Евклида имеет структуру {4, 4}, мы уже знаем, что есть ещё всего две структуры этой же плоскости {3, 6} и {6, 3}. Теперь мы узнали, что разбиение 3-мерного Евклидова пространства единственно {4, 3, 4} — на кубы, сходящиеся по 4 штуки в ребре. Мы представляем мысленно это разбиение и ощущаем структуру этого пространства. Теперь представим мысленно {5 ,3} — додекаэдры, приложим их между собой по плоским граням (пятиугольникам), в ребре сойдётся 3 таких додекаэдра и ещё останется зазор. Теперь мысленно равномерно раздуем эти додекаэдры до тех пор, пока зазор не исчезнет. Когда он исчезнет, то в ребре сойдутся ровно 3 додекаэдра. Теперь мысленно сложим по три додекаэдра в каждом ребре. Во всех рёбрах одновременно это представить уже сложнее, но нужно. Если взять 120 таких раздутых додекаэдров и приложить их все без зазоров между собой по граням, то получим замкнутое разбиение 3-мерной сферы. Так же можно воображать с другими 5-тью разбиениями 3-мерной сферы. Такие рассудительные эксперименты с многогранниками помогают мысленно понять структуру 3-мерной сферы и прикоснуться к 4-мерному пространству Евклида. Аналогично можно поразмышлять с гиперболическим 3-мерным пространством. Приведённые в публикации выкладки помогают понять в каком пространстве мы находимся, для заданного символа Шлефли, т.е. для заданного мысленного построения.
В следующей публикации мы проделаем всё тоже самое только на одну размерность выше. Думаю, что дам там видео ролик поясняющий основную идею перехода (подъёма) по размерностям. Если кто-то ещё не понял, что происходит, то возможно этот ролик прольёт свет на все проделанные выкладки тут и в предыдущей статье.
Если всё понятно, то переходите на следующий уровень по размерности.
Автор: anegrey






