Иногда возникает необходимость ускорить вычисления, причем желательно сразу в разы. При этом приходится отказываться от удобных, но медленных инструментов и прибегать к чему-то более низкоуровневому и быстрому. R имеет довольно развитые возможности для работы с динамическими бибиотеками, написанными на С/С++, Fortran или даже Java. Я по привычке предпочитаю С/С++.
R и С
Сразу оговорюсь, что я работаю под Debian Wheezy (под Windows, вероятно, есть какие-то ньюансы). При написании библиотеки на С для R надо учитывать следующее:
- Функции, написанные на С и вызываемые в R, должны иметь тип void. Это значит, что если функция возвращает какие-то результаты, то их надо вернуть через аргументы функции
- Все аргументы передаются по ссылке (а при работе с указателями надо не терять бдительность!)
- В С код желательно включать
R.hиRmath.h(если используются математические функции R)
Начнем с простой функции, которая вычисляет скалярное произведение двух векторов:
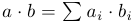
#include <R.h>
void iprod(double *v1, double *v2, int *n, double *s) {
*s = 0;
for (int i = 0; i < *n; i++) {
*s += v1[i] * v2[i];
}
}
Далее надо получить динамическую библиотеку — можно непосредственно через gcc, а можно воспользоваться такой командой (кстати, стоит запомнить вывод, т.к. он пригодится нам в дальнейшем):
R CMD SHLIB inner_prod.c
На выходе получим файл inner_prod.so, для загрузки которого воспользуемся функцией dyn.load(). Для вызова же самой функции на С используем .C() (есть еще .Call() и .External(), но с несколько другим функционалом, причем между сторонниками .C() и .Call() подчас идут жаркие споры ). Отмечу только, что при написании кода на С для вызова через .C() он получается более чистым и удобочитаемым. Особое внимание стоит обратить на соответствие типов переменных в R и C (в документации по функции .C() об этом подробно написано). Функция-обертка на R:
iprodс <- function(a, b) {
if (!is.loaded('iprod')) {
dyn.load("inner_prod.so")
}
n <- length(a)
v <- 0
return(.C("iprod", as.double(a), as.double(b), as.integer(n), as.double(v))[[4]])
}
Теперь можно узнать, чего же мы добились:
> n <- 1e7; a <- rnorm(n); b <- rnorm(n);
> iprodс(a, b)
[1] 3482.183
И небольшая проверка:
> sum(a * b)
[1] 3482.183
Во всяком случае, считает правильно.
R и СUDA
Чтобы воспользоваться всеми благами, которые предоставляет графический ускоритель Nvidia, в Debian, необходимо, чтобы были установлены проприетраный драйвер Nvidia и пакет nvidia-cuda-toolkit. CUDA, безусловно, заслуживает отдельной огромной темы, и так как мой уровень в этой теме «новичок», я не буду пугать людей своим кривым и недописаным кодом, а позволю себе скопировать несколько строк из методички.
Предположим, необходимо каждый элемент вектора возвести в третью степень и найти евклидову норму полученного вектора:
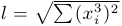
Чтобы несколько облегчить работу с GPU, воспользуемся библиотекой параллельных алгоритмов Thrust, которая позволяет абстрагироваться от низкоуровневых операций CUDA/C. При этом данные представляются в виде векторов, к которым применяются некоторые стандартные алгоритмы (elementwise operations, reductions, prefix-sums, sorting).
#include <thrust/transform_reduce.h>
#include <thrust/device_vector.h>
#include <cmath>
// Функтор, выполняющий возведение числа в 6 степень на GPU (device)
template <typename T>
struct power{
__device__
T operator()(const T& x) const{
return std::pow(x, 6);
}
};
extern "C" void nrm(double *v, int *n, double *vnorm) {
// Вектор, хранимый в памяти GPU, в который копируется содержимое *v
thrust::device_vector<double> dv(v, v + *n);
// Reduce-трансформация вектора, т.е. сначала к каждому члену вектора применятся функтор power
// потом полученные числа складываются.
*vnorm = std::sqrt( thrust::transform_reduce(dv.begin(), dv.end(), power<double>(), 0.0, thrust::plus<double>()) );
}
Использование extern "C" тут обязательно, иначе R не увидит функцию nrm(). Для компиляции кода теперь будем использовать nvcc. Помните вывод команды R CMD SHLIB...? Вот его немного и адаптируем, чтобы библиотека, использующая CUDA/Thrust без проблем вызывалась из R:
nvcc -g -G -O2 -arch sm_30 -I/usr/share/R/include -Xcompiler "-Wall -fpic" -c thr.cu thr.o
nvcc -shared -lm thr.o -o thr.so -L/usr/lib/R/lib -lR
На выходе получим DSO thr.so. Функция-обертка практически ничем не отличается:
gpunrm <- function(v) {
if (!is.loaded('nrm'))
dyn.load("thr.so")
n <- length(v)
vnorm <- 0
return(.C("nrm", as.double(v), as.integer(n), as.double(vnorm))[[3]])
}
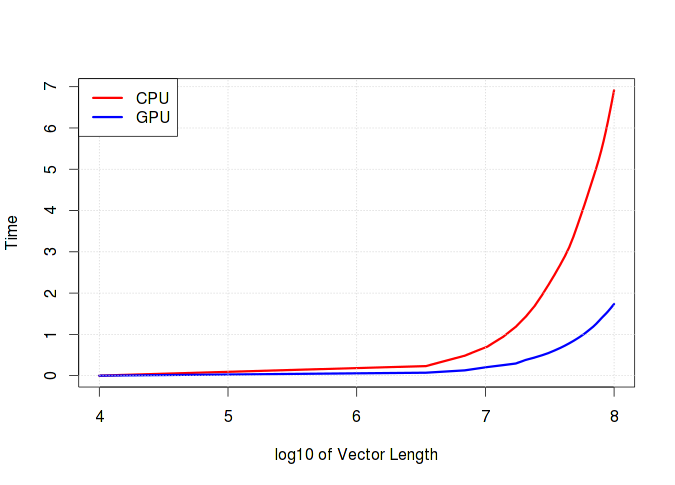
Ниже на графике хорошо видно, как растет время выполнения в зависимости от длины вектора. Стоит отметить, что если в вычислениях преобладают простые операции типа сложения/вычитания, то разницы между временем счета на CPU и GPU практически не будет. Более того, очень вероятно, что GPU проиграет из-за накладных расходов по работе с памятью.
gpu_time <- c()
cpu_time <- c()
n <- seq.int(1e4, 1e8, length.out=30)
for (i in n) {
v <- rnorm(i, 1000)
gpu_time <- c(gpu_time, system.time({p1 <- gpunrm(v)})[1])
cpu_time <- c(cpu_time, system.time({p2 <- sqrt(sum(v^6))})[1])
}
Заключение
На самом деле в R операции для работы с матрицами и векторами очень хорошо оптимизированы, и необходимость в использовании GPU в обычной жизни возникает не так уж и часто, но иногда GPU позволяет заметно сократить время расчета. В CRAN уже есть готовые пакеты (например, gputools), адаптированные для работы с GPU (тут можно почитать про это подробнее).
Ссылки
1. An Introduction to the .C Interface to R
2. Calling C Functions in R and Matlab
3. Writing CUDA C extensions for R
4. Thrust::CUDA Toolkit Documentation
Автор: kxx
