Этот пост про относительно новый метод обработки сигналов, описанный в статье Adaptive data analysis via sparse time-frequency representation, а также про крохотную, но сбившую лично меня с толку, ошибку. Сию статью опубликовали в 2011 году профессора прикладной математики Калифорнийского Технологического института Томас И. Хоу и Зуокьянг Ши, и, вероятно, к моменту, как вы это читаете, они уже её поправили.
На эту статью я наткнулся в поиске различных методов частотно-временного анализа нелинейных и нестационарных сигналов — в моем случае ультразвуковых сигналов от передвигающихся форменных элементов крови в сосудах человека. Суть такого анализа состоит в отслеживании изменений характеристик сигнала, иначе говоря, мы хотим знать зависимость составляющих сигнал частот от времени. За исключением широко распространенных методов — спектрального и вейвлет-анализа, были найдены такие методы как EMD (разложение на эмпирические моды) и синусоидальное моделирование, о котором далее пойдет здесь речь.
Метод эмпирических мод довольно прост в применении, однако не особо развит с точки зрения обоснованности полученных результатов. Томас Хоу и Зуокьянг Ши пошли дальше в развитии математического аппарата и предложили свой метод синусоидального моделирования сигнала. Его идея заключается в разреженной декомпозиции сигнала на гармоники с гладкими амплитудами. Какой результат мы ожидаем получить — на картинке выше. В данном случае раскладывался сигнал, полученный функцией f(t) = 6t + cos(8πt) + 0.5 cos(40πt). Разложение сигнала, естественно, не уникально, поэтому был введен критерий минимума составляющих гармоник, и задача сформировалась следующим образом:

Решением задачи P0 будут гармоники c амплитудами a и фазовыми функциями theta, чьи производные будут соответствовать частотам сигнала. Авторы предлагают решать эту задачу рекурсивно: извлекаем одну гармоническую составляющую, получаем остаток (медиану) — работаем с ним, извлекаем из него следующую гармонику, получаем остаток и так далее. Так как медиана должна быть гораздо более гладкой, чем сигнал, нахождение гармоники сводится к решению следующей задачи:
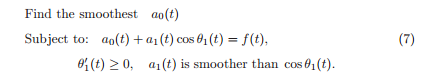
где a1*cos(theta1(t)) — полученная гармоника, a0 — медиана. Гладкость амплитуды определяется общей вариацией:
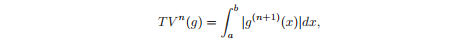
Чем больше гладкость функции g, тем ближе к нулю её (n+1) производная, тем, соответственно, меньше общая вариация n-го порядка. Можно сказать еще так: чем меньше порядок полинома, которым мы можем интерполировать, тем глаже функция. Логично предположить, что лучше всего будет искать минимум вариации нулевого порядка, однако, в этом случае мы рискуем получить кусочно-постоянную функцию (staircase effect) и потерять некоторую нужную нам информацию более высокого порядка (например, кривизну). Авторы статьи предлагают уменьшать вариацию третьего порядка, устремляя четвертые производные к нулю, тем самым делая нечто похожее на аппроксимацию кубическими сплайнами. В результате, мы ищем min TV^3(a0). Но нам также важно, чтобы и a1 была достаточно гладкой, поэтому в лучшем случае мы должны найти min TV^3(a0) + min λ*TV^3(a1), где λ — множитель Лагранжа, играющий в данном случае роль весового коэффициента. Для упрощения авторы оставили λ = 1 и пришли к следующей задаче:
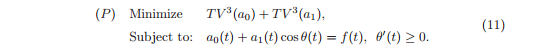
Алгоритм
Для решения этой задачи предложен итеративный алгоритм. В условии добавляется еще одна гармоника — b1*sin(theta1(t)), её гладкость также становится нашей целью. Инициализируем фазовую функцию theta^0 таким образом, чтобы она была возрастающей функцией, удовлетворяющей условию cos(theta^0) = f(t), и запускаем основную итерацию:

На первом шаге минимизируем общие вариации амплитуд. На следующем — обновляем theta по вышеозначенной формуле, затем проверяем, насколько она изменилась. К концу алгоритма предполагается, что амплитуда b1 будет уже пренебрежимо мала, соответственно, мал будет artcg(b1/a1), и theta сойдется к какому-то значению. Это и будет наша фазовая функция. Получив theta^n, мы выделяем первую гармонику a1*cos(theta1(t)), где theta1 = theta^n. Далее запускаем этот алгоритм на остатке, то есть работаем со значениями f(t) = a0 + b1 * sin(theta1(t)). Выделяем следующую гармонику a2*cos(theta2(t)), продолжаем с остатком. И так до тех пор, пока норма остатка не будет пренебрежимо мала. Я брал первую норму. Для тех, кто не помнит её определение:
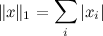
Для применения задачу нахождения минимума общей вариации авторы свели к задаче L1-минимизации, заменив дифференциальное уравнение разностным. У нас имеется сигнал, а точнее упорядоченный набор из N точек (узлов), который мы хотим разложить, то есть представить как сумму векторов a0, a1*cos(theta1(t)) и b1*sin(theta1(t)). И в переформулированной задаче была замечена злосчастная опечатка:

Предполагая, что a0^n, a1^n, b1^n — сеточные функции, мы аппроксимируем их четвертые производные умножением их на матрицу D^4. Затем, минимизируя сумму модулей полученных значений, мы уменьшаем соответствующие вариации. Все логично и правдоподобно, но, реализовав сей алгоритм, я ужаснулся, увидев результаты — получалось нечто совершенно хаотическое. Долго пытаясь обнаружить ошибку в коде, я, наконец, осознал, что ошибка была в статье.
Дело в том, что при умножении Phi на x мы получаем вектор, где элементами являются суммы производных a0^n, a1^n, b1^n в соответствующих точках. То есть мы минимизируем общую вариацию от (a0^n + a1^n + b1^n), а не сумму трех вариаций, как было указано сверху.
Ошибка есть ошибка, нашел, исправил и забыл на несколько месяцев. И вот на майских праздниках меня все-таки дернуло написать письмо профессорам с предложением заменить в статье min ||Phi*x|| на min ||D^4*a0^n|| + ||D^4*a1^n|| + ||D^4*b1^n||. Удивительно, уже через час пришел ответ от профессора Хоу с фразой «Thanks for your email. We will study your note and get back to you soon» и простой подписью «Tom».
Еще через 6 часов пришло письмо от профессора Ши:
Dear Aleksandr,
Thanks a lot for your email. We did make a typo here.
Phi should be diag(D4,D4,D4) which was also what we used in the
algorithm. Thanks.Best,
Zuoqiang Shi
Естественно, моя поправка и то, что они хотели написать, идентичны. Единственное, должен заметить, что, если не хранить матрицу Phi в предположении, что она разряженная, то есть хранить кучу нулевых элементов, память может скоро закончиться.
Как решается задача L1-минимизации
Для своего алгоритма профессора предлагают методы split Bregman iteration и L1-regularized least square method. Однако, эти методы достаточно свежи и, вероятно, зашиты далеко не во все пакеты. Кому лениво (как мне), реализовывать какой-нибудь из алгоритмов нахождения минимума первой нормы, тому будет полезно узнать, как эта задача сводится к более распространенной задаче линейного программирования. Исходная задача выглядит следующим образом:
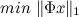
при условии
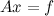
где А — матрица NxM, Phi — матрица KxM, x — вектор размерности M.
Она эквивалентна следующей задаче линейного программирования:
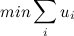
при условиях
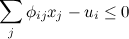
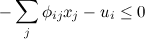
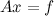
где phi(i,j) — элементы матрицы Phi.
Формально переход можно сделать следующим образом. К вектору x добавляется K переменных, тем самым он становится размерности K+M:
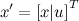
К матрице А добавляется нулевая матрица размерностью NxK:
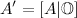
Вектор с (коэффициенты в задаче ЛП) состоит из M нулей и K единиц:
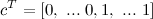
Матрица F составляется из матрицы Phi и единичной матрицы I. Размерность F — (2*K)x(M+K):
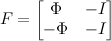
Таким образом, формализованная задача выглядит так:
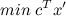
при условиях
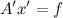
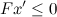
Результаты
Вот каковы результаты работы алгоритма для ранее указанного примера f(t) = 6t + cos(8πt) + 0.5 cos(40πt). На графиках полученные этим алгоритмом значения (синие) сравниваются с аналитическими значениями (красные) и значениями, полученными разложением на эмпирические моды (черные).
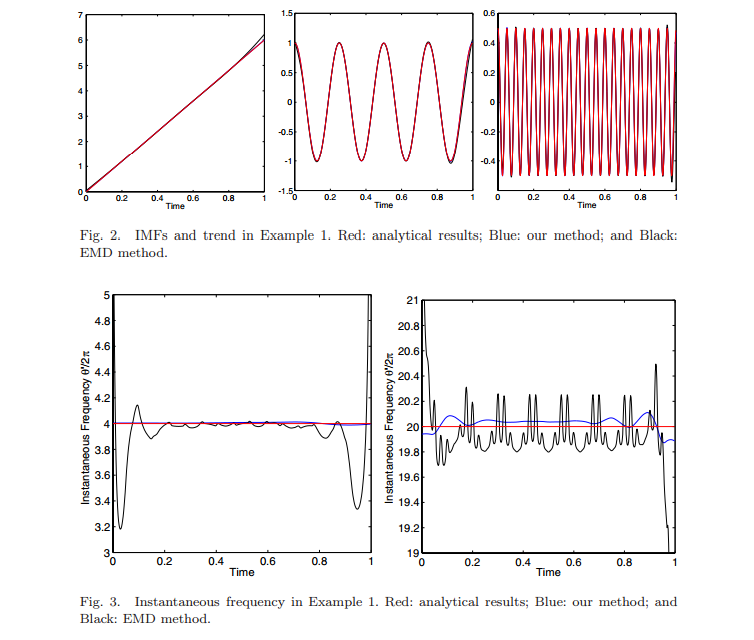
На следующем примере видно, как этот метод помогает отслеживать частотные изменения сигнала.
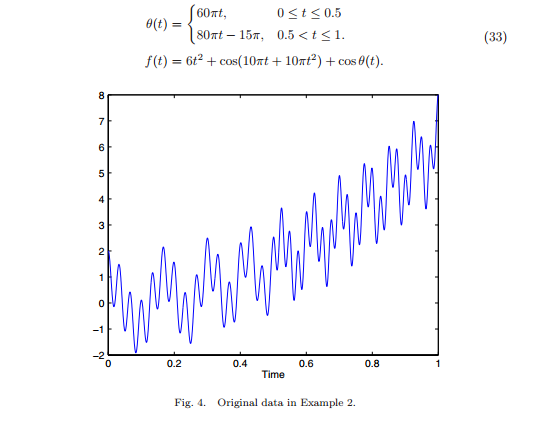
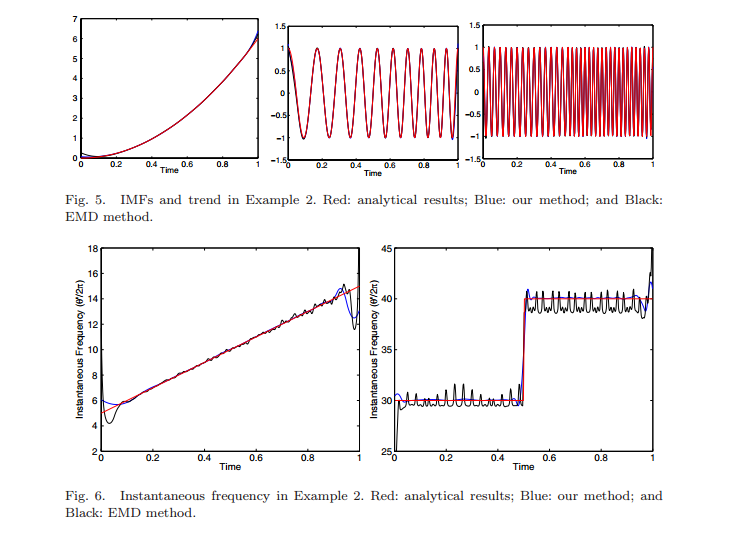
В статье указаны и другие примеры, а также результаты работы алгоритма на реальных данных.
Итог
Алгоритм весьма интересен и, на мой взгляд, требует дальнейшего анализа, благо простора для раздумий здесь полно. Его явными минусами являются большая вычислительная сложность, а также чувствительность к шуму и, как следствие, нестабильная работа при зашумленных данных. Авторы предлагают разрешать проблему чувствительности при помощи низкочастотной фильтрации и преобразования Фурье. Но об этом в другой раз.
Напоследок хочется лишний раз похвастаться и сказать, что, видимо, и такое случается, что профессора в Калтехе допускают пускай и ничтожные, но ошибки, и русский студент, не имеющий пока и бакалавра, может им на это указать.
Автор: The_Freeman