О прямоугольных координатах и гексагональных сетках

Думаю, никому не нужно объяснять, насколько широко в играх (и не только) используются гексагональные сетки. Как для заданной шестиугольной ячейки найти координаты ее центра и вершин — достаточно очевидно. Обратное же преобразование (т.е. поиск ячейки, в которую попала данная точка с координатами x и y) уже не столь тривиально. О нём и пойдет речь в данном топике.

Пролог

У меня есть давняя мечта: написать интересную игру. К результату я иду очень медленно и, быть может, не совсем верно, но здесь речь пойдет не об этом. В очередной период свободного времени я захотел проработать кое-какую концепцию будущей игры, основанную на гексагональной сетке. Будучи на даче и без какого-либо признака интернета, я вынужден был сам искать алгоритм преобразования между «шестиугольными» и прямоугольными координатами. Позже я сравнил то, что получилось с известными алгоритмами и оказался приятно удивлен: самые первые ссылки в гугле по запросу «pixel to hexagon» выдавали описания алгоритмов, гораздо более трудоемких и запутанных, чем мой. Способ, эквивалентный моему, я нашел здесь.

По теме

Описание сетки

Для начала, различим два способа ориентировать шестиугольную ячейку относительно прямоугольных координат:

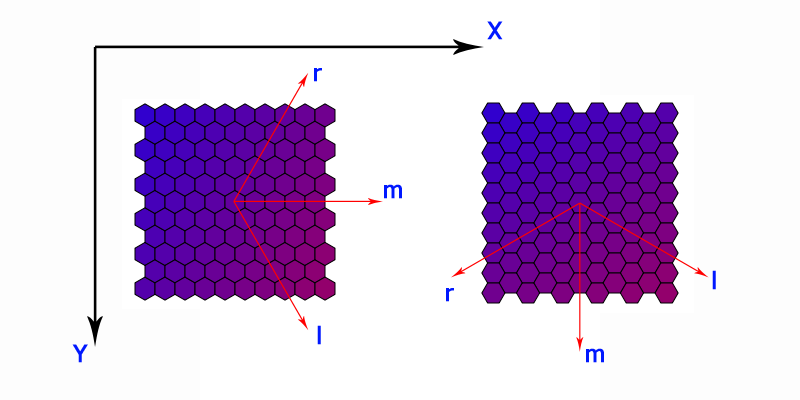
Оси я назвал буквами «m», «l» и «r» от main, left и right. (Первоначально это все было проделано на листочке, где m совпадало с осью x, а ось y смотрела вверх — поэтому «лево» и «право» здесь довольно-таки условны.) Таким образом, ось m совпадает с одной из прямоугольных осей; ось l повернута на 60 градусов относительно этой прямоугольной оси и на 30 градусов относительно второй прямоугольной оси; ось r составляет 60 градусов с первой прямоугольной осью и 150 градусов со второй. Нумерация ячеек идет вдоль осей m и l.

Для реализации сетки я написал «полевой менеджер» — класс, объект которого хранит информацию об ориентации и периоде решетки.

// В данном примере я использовал Qt-шные классы, но,
// т.к. в будущем не планирую их использовать, сделал
// соответствующие typedef-ы.
typedef QPointF MyPointF;
typedef QPoint MyPointI;

// Объявляем наш менеджер
class FieldManager
  {
  public:
  // Прямоугольная ось, вдоль которой направлена ось m.
    enum Orientation
      {
      OX,
      OY
      };

    // Конструктор по умолчанию.
    FieldManager(double period = 1, Orientation orientation = OX);

    // Метод получения координаты центра данной ячейки (прямое преобразование).
    MyPointF CellCenter(int m, int l) const;
    // Метод поиска ячейки, в которую попала точка (x, y) (обратное преобразование).
    MyPointI CellInd(double x, double y) const;

  private:
    // Период решетки.
    double m_period;
    // Ориентация решетки.
    Orientation m_orientation;
  };

Прямое преобразование

// Для начала введем константы, чтобы
// миллион раз не считать проекции.
const double sin60 = sqrt(3.0) * 0.5;
const double cos60 = 0.5;
const double sin30 = cos60;
const double cos30 = sin60;

// Реализуем конструктор.
FieldManager::FieldManager(double period, Orientation orientation)
  : m_period(period), m_orientation(orientation)
  {
  }

// Прямое преобразование. Здесь никаких хитростей.
MyPointF FieldManager::CellCenter(int m, int l) const
  {
  double along_coord = m_period * (m + l * cos60);
  double other_coord = m_period * l * sin60;
  if (m_orientation == OX)
    return MyPointF(along_coord, other_coord);
  else
    return MyPointF(other_coord, along_coord);
  }

Обратное преобразование

С обратным же преобразованием я мучался долго. Очень не хотелось пихать в программу громоздкие циклы или условные операторы. Видно было, что изолинии осей m, l и r (т.е. множества точек с постоянными значениями координат, соответствующими этим осям) разбивают плоскость на множество треугольников (в качестве шага по каждой из осей я использовал половину периода):

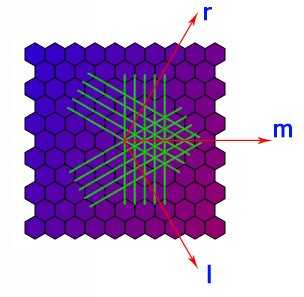
Таким образом, каждому треугольнику ставится в соответствие три числа. Оставалось только придумать операцию, которая сгруппирует эти треугольники по шесть на один шестиугольник. Очевидно также, что преобразование должно быть линейным, т.к. размеры сетки не меняются в пространстве. В итоге, правильное преобразование было мной найдено:

// Обратное преобразование.
MyPointI FieldManager::CellInd(double x, double y) const
  {
  // Выбираем правильную ориентацию.
  double along_coord = (m_orientation == OX) ? x : y;
  double other_coord = (m_orientation == OX) ? y : x;
  
  // Считаем проекции на оси m, l и r (в половинах периода решетки).
  // Здесь можно было обойтись меньшим количеством операций,
  // засунув, например, двойку и период решетки под косинусы и синусы
  // в отдельные константы
  int m = floor(2 * along_coord / m_period);
  int l = floor(2 * (cos60 * along_coord + sin60 * other_coord) / m_period);
  int r = floor(2 * (cos60 * along_coord - sin60 * other_coord) / m_period);

  // И, собственно, сам финт ушами:
  return MyPointI( floor((m + r + 2) / 3.0), 
                   floor((l - r + 1) / 3.0));
  }

Чтобы найти это преобразование, мне помогли следующие действия: я расчертил на бумажке сетку из этих треугольников, затем выделил на ней «линии» из шестиугольников с постоянным (с учетом округления) значением m и посмотрел, что объединяет получившиеся треугольники. Затем сделал то же самое для оси l. Видно было, что для полосы шестиугольников, направленной вдоль оси l, оси m и r разбивают пространство на ромбики, не пересекающие данную полосу (т.е. лежащие целиком внутри или снаружи от нее). Причем при фиксированном m данной полосе соответствуют три ромбика с различными l и наоборот. Отсюда и взялось округление от деления на 3. Аналогично для другого набора полос.

Заключение

На этой ноте данное повествование заканчивается. Благодарю всех, кто не обделил вниманием. Надеюсь, смог кому-нибудь помочь.

P. S.
Также надеюсь, что игра когда-нибудь увидит свет и здесь про нее также появится статья.

Автор: SiLiKhon