Разбор задачи с собеседования Google: поиск соотношения

Добро пожаловать в очередную из серии статей с разбором задачек, которые я задавал на собеседованиях в Google, прежде чем их запретили после утечки. С тех пор я оставил работу инженера-программиста в Google и перешёл на должность менеджера по разработке в Reddit, но у меня всё ещё осталось несколько замечательных тем. К настоящему моменту мы разобрали динамическое программирование, возведение матриц в степень и синонимичность запросов. На этот раз совершенно новый вопрос.

Но сначала два замечания. Во-первых, работа в Reddit была потрясающей. Последние восемь месяцев я строил и возглавлял новую команду Ads Relevance и занимался организацией нового офиса разработки в Нью-Йорке. Как бы это ни было весело, к сожалению, я обнаружил, что до недавнего времени у меня не оставалось времени или энергии на блог. Боюсь, что я немного забросил эту серию. Извините за задержку.

Во-вторых, если вы следили за статьями, то после последнего выпуска могли подумать, что я начну копаться в вариантах синонимичности запросов. Хотя я хотел бы когда-то вернуться к этому, но должен признаться, что из-за смены работы потерял должный интерес к этой проблеме и пока решил отложить её. Впрочем, оставайтесь на связи! За мной должок, и я намерен его вернуть. Просто, ну знаете, чуть позже…

Быстрый отказ от ответственности: хотя собеседование кандидатов является одной из моих профессиональных обязанностей, этот блог представляет мои личные наблюдения, личные истории и личное мнение. Пожалуйста, не принимайте это за какое-либо официальное заявление от Google, Alphabet, Reddit или любого другого лица или организации.

Поиск нового вопроса

В предыдущей статье я описал один из своих любимых вопросов, который использовал в течение длительного времени, до неизбежной утечки. Предыдущие вопросы были увлекательными с теоретической точки зрения, но я хотел выбрать проблему, чуть более актуальную для Google как компании. Когда этот вопрос запретили, то я хотел найти замену с учётом нового ограничения: чтобы вопрос был проще.

Теперь это может показаться немного удивительным, учитывая печально известный процесс собеседований в Google. Но в то время более простая проблема имела смысл. Мои рассуждения состояли из двух частей. Первая прагматичная: кандидаты обычно не очень хорошо справлялись с предыдущими вопросами, несмотря на многочисленные намёки и упрощения, и я не всегда был полностью уверен, почему. Вторая теоретическая: процесс собеседования должен разделять кандидатов на категории «стоит нанимать» и «не стоит нанимать», и мне было любопытно, можно ли сделать это с вопросом немного попроще.

Прежде чем разъяснить эти два пункта, хочу указать на то, что они не означают. «Я не всегда уверен, почему у человека возникают проблемы» не означает бесполезность вопросов и что я хотел упростить собеседование по этой причине. Даже с самым сложным вопросом многие хорошо справлялись. Я имею в виду то, что когда у кандидатов возникали проблемы, мне бывало трудно понять, чего им не хватает.

Хорошие интервью дают широкую картину сильных и слабых сторон кандидата. Для комитета по найму недостаточно просто сказать, что «он провалился»: комитет определяет, есть ли у кандидата специфические для компании качества, которые они ищут. Точно так же слова «он крут» не помогают комитету принять решение по кандидату, который силён в некоторых областях, но сомнителен в других. Я обнаружил, что более сложные вопросы слишком часто разделяют кандидатов по этим двум категориям. В этом свете «я не всегда уверен, почему у человека возникают проблемы» означает «неспособность продвинуться в этом вопросе сама по себе не рисует картину способностей этого кандидата».

Классификация кандидатов как «стоит нанимать» и «не стоит нанимать» не означает, что процесс собеседования должен отделять глупых кандидатов от умных. Я не могу вспомнить ни одного кандидата, который не был бы умным, талантливым и мотивированным. Многие пришли из отличных университетов, а остальные явно были исключительно мотивированы. Проход через телефонные собеседования — уже хорошее сито, и даже отказ на этом этапе не является признаком отсутствия способностей.

Однако я могу вспомнить многих, кто не был достаточно подготовлен к интервью или работал слишком медленно, или требовал слишком большого надзора для решения проблемы, или общался неясным образом, или не смог перевести свои идеи в код, или придерживался позиции, которая просто не привела бы его к успеху в долгосрочной перспективе и т. д. Определение «стоит нанять» размытое и варьируется в зависимости от компании, а процесс собеседования и заключается в том, чтобы определить соответствие каждого кандидата требованиям конкретной компании.

Я прочитал много комментариев reddit с жалобами на излишне сложные вопросы собеседования. Мне стало любопытно, можно ли по-прежнему сделать рекомендацию «достоин/не достоин» на более простой задаче. Я подозревал, что это даст полезный сигнал без лишней трепли нервов кандидата. Расскажу о своих выводах в конце статьи…

С этими мыслями я искал новый вопрос. В идеальном мире это достаточно простой вопрос, чтобы решить его за 45 минут, но с дополнительными вопросами, чтобы более сильные кандидаты проявили свои навыки. Он также должен быть компактным в реализации, потому что многие кандидаты по-прежнему пишут на доске. Большой плюс, если тема будет как-то связана с продуктами Google.

Наконец, я остановился на вопросе, который какой-то замечательный гуглер тщательно описал и вставил в нашу базу данных вопросов. Сейчас я проконсультировался с бывшими коллегами и убедился, что вопрос по-прежнему запрещён, поэтому вам его точно не зададут на собеседовании. Представляю его в таком виде, в каком он кажется мне наиболее эффективным, с извинениями перед оригинальным автором.

Вопрос

Поговорим об измерении расстояний. Хэнд — это единица измерения в четыре дюйма, которая обычно используется в англоязычных странах для измерения высоты лошадей. Световой год — ещё одна единица измерения, равная расстоянию, которое частица (или волна?) света пройдёт за определённое количество секунд, примерно равное одному земному году. На первый взгляд, у них мало общего друг с другом, кроме того, что они используются для измерения расстояния. Но оказывается, что Google может довольно легко их конвертировать:

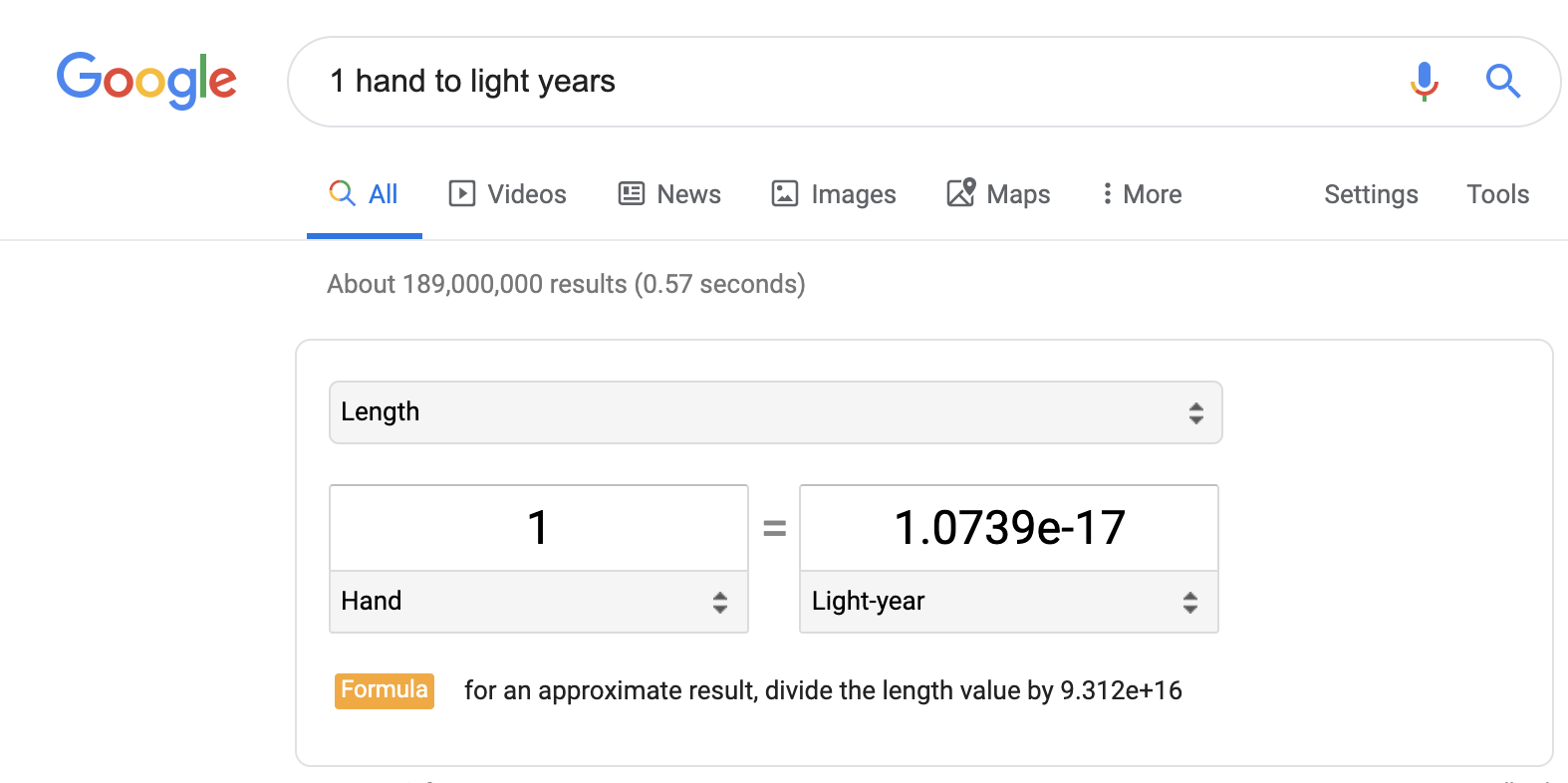
Это может показаться очевидным: в конце концов, они обе измеряют расстояние, поэтому ясное дело, что есть преобразование. Но если подумать, немного странно: как они вычислили этот коэффициент конверсии? Ясно, что никто на самом деле не считал количество хэндов в световом году. На самом деле не нужно считать это напрямую. Вы можете просто использовать общеизвестные преобразования:

• 1 хэнд = 4 дюйма
• 4 дюйма = 0,33333 фута
• 0,33333 фута = 6,3125e−5 миль
• 6,3125e−5 миль = 1,0737e−17 световых лет

Цель задачи — разработать систему, которая выполнит это преобразование. В частности:

Приведите список коэффициентов пересчёта (отформатированный на выбранном вами языке) в виде набора начальных единиц измерения, конечных единиц и множителей, например:

фут дюйм 12
фут ярд 0,3333333
и т. д.

Таким образом, чтобы ORIGIN * MULTIPLIER = DESTINATION. Разработайте алгоритм, который принимает два произвольных значения единиц измерения и возвращает коэффициент преобразования между ними.

Обсуждение

Мне нравится эта проблема, потому что у неё интуитивно понятный и очевидный ответ: просто конвертировать из одного единицы в другую, потом в следующую, пока не найдёте цель! Не могу вспомнить ни одного кандидата, который столкнулся с этой проблемой и был полностью озадачен, как её решить. Это хорошо соответствует требованию «более простой» проблемы, поскольку предыдущие обычно требовали длительного изучения и размышлений, прежде чем находился хотя бы базовый подход к решению.

И всё же многие кандидаты не смогли реализовать интуицию в виде рабочего решения без явных намёков. Одно из достоинств этого вопроса в том, что он проверяет способность кандидата сформулировать проблему (сделать фрейминг) таким образом, чтобы она поддавалась анализу и кодированию. Как мы увидим, здесь есть одно очень интересное расширение, которое требует нового концептуального скачка.

Для контекста, фрейминг — это акт перевода проблемы с неочевидным решением в эквивалентную проблему, где решение выводится естественным путём. Если это звучит совершенно абстрактно и неприступно, простите, но так и есть. Я объясню, что имею в виду, когда представлю начальное решение этой проблемы. Первая часть решения будет упражнением в разработке и применении алгоритмических знаний. Вторая часть будет упражнением в манипулировании этим знанием, чтобы прийти к новой и неочевидной оптимизации.

Часть 0. Интуиция

Прежде чем копнуть глубже, давайте полностью исследуем «очевидное» решение. Большинство требуемых преобразований просты и понятны. Любой американец, который путешествовал за пределами США, знает, что большая часть мира для измерения расстояний использует таинственную единицу «километр». Для преобразования нужно всего лишь умножить количество миль примерно на 1,6.

С такими вещами мы сталкиваемся на протяжении большей части жизни. Для большинства единиц измерения уже есть предварительно вычисленное преобразование, так что нужно лишь посмотреть его в соответствующей таблице. Но если нет прямого преобразования (например, из хэндов в световые годы), есть смысл построить путь преобразования, как указано выше:

• 1 хэнд = 4 дюйма
• 4 дюйма = 0,33333 фута
• 0,33333 фута = 6,3125e−5 миль
• 6,3125e−5 миль = 1,0737e−17 световых лет

Это было совсем просто, я просто придумал такое преобразование, используя своё воображение и стандартную таблицу преобразований! Однако остаются некоторые вопросы. Есть ли более короткий путь? Насколько точен коэффициент? Всегда ли возможно преобразование? Можно ли его автоматизировать? К сожалению, здесь наивный подход ломается.

Часть 1. Наивное решение

Приятно, что проблема имеет интуитивное решение, но на самом деле эта простота является препятствием для решения проблемы. Нет ничего труднее попыток понять по-новому то, что вы уже понимаете — не в последнюю очередь потому, что вы часто знаете меньше, чем думаете. Для иллюстрации, представьте, что вы пришли на интервью — и у вас в голове этот интуитивный метод. Но он не позволяет решить ряд важных проблем.

Например, что делать, если нет преобразования? Очевидный подход ничего не говорит, действительно ли возможно преобразование из одной единицы в другую. Если мне дадут тысячу коэффициентов конверсии, мне будет очень трудно определить, возможно ли оно в принципе. Если меня просят сделать преобразование между незнакомыми (или выдуманными) единицами укачки и уколки, то я без понятия, с чего начать. Как здесь поможет интуитивный подход?

Должен признать, что это своего рода надуманный сценарий, но есть и более реалистичный. Видите, что моя постановка задачи включает только единицы расстояния. Это сделано специально. Что, если я попрошу систему перевести из дюймов в килограммы? И вы, и я знаем, что это невозможно, потому что они измеряют разные типы, но входные данные ничего не говорят о «типе», который измеряет каждая единица.

Именно здесь тщательная постановка вопроса позволяет проявить себя сильным кандидатам. Перед разработкой алгоритма они продумывают крайние случаи системы. И такая постановка проблемы целенаправленно даёт им возможность спросить меня, будем ли мы переводить разные единицы. Это не такая огромная проблема, если она встретится на ранней стадии, но всегда хороший знак, когда кто-то заранее спрашивает меня: «Что должна вернуть программа, если преобразование невозможно?» Постановка вопроса таким образом даёт мне представление о способностях кандидата, прежде чем он напишет хотя бы одну строку кода.

Представление в виде графа

Очевидно, что наивный подход не подходит, поэтому мы должны подумать, как можно произвести такую конверсию? Ответ — рассмотреть единицы как график. Это первый скачок понимания, необходимый для решения этой задачи.

В частности, представьте, что каждая единица является узлом в графе, и существует ребро от узла A до узла B, если A можно преобразовать в B:

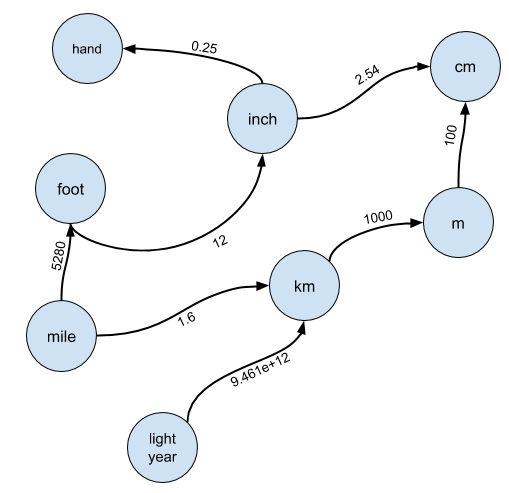
Края помечены коэффициентом конверсии, на который вы должны умножить A, чтобы получить B.

Я почти всегда ожидал, что кандидат придумает такой фрейминг, и редко давал серьёзные подсказки для него. Я могу простить кандидата, который не замечает решения проблемы с использованием непересекающихся множеств или не слишком глубоко знаком с линейной алгеброй, чтобы реализовать решение, сводящееся к повторному возведению в степень матрицы смежности, но на любой учебной программе или курсе по программированию преподаются графы. Если у кандидата нет соответствующих знаний, это сигнал «не стоит нанимать».

В любом случае

Представление в виде графа сводит решение к классической проблеме поиска графа. В частности, здесь полезны два алгоритма: поиск в ширину (BFS) и поиск в глубину (DFS). При поиске в ширину мы исследуем узлы в соответствии с их расстоянием от начала координат:

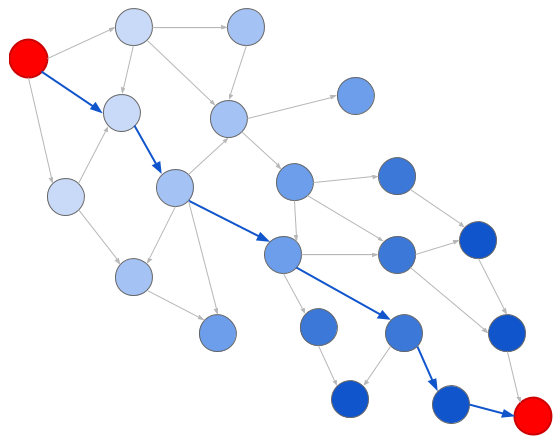
Более тёмные синие цвета означают более поздние поколения

А при поиске в глубину мы исследуем узлы в том порядке, в каком они встречаются:

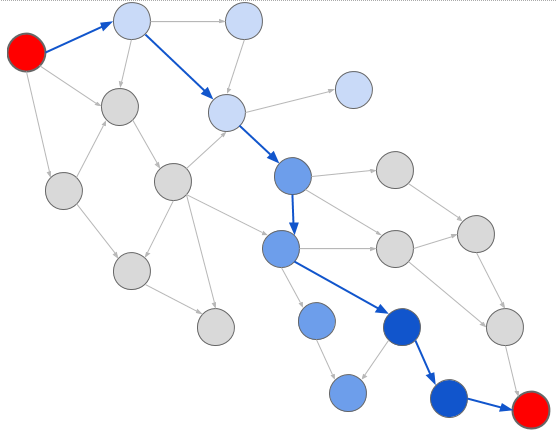
Более тёмные синие цвета также означают более поздние поколения. Обратите внимание, что мы на самом деле не посещаем все узлы

Любой из алгоритмов легко определяет, существует ли преобразование из одной единицы в другую, достаточно просто выполнить поиск по графу. Начинаем с исходной единицы и ищем, пока не найдём единицу назначения. Если не удаётся найти пункт назначения (как при попытке преобразовать дюймы в килограммы), мы знаем, что пути нет.

Но подождите, чего-то не хватает. Мы не хотим искать, существует ли путь, мы хотим найти коэффициент конверсии! Именно здесь кандидат должен совершить скачок: оказывается, вы можете модифицировать любой алгоритм поиска для вычисления коэффициента конверсии, просто сохранив дополнительное состояние по мере прохождения. Вот где иллюстрации перестают иметь смысл, так что давайте погрузимся прямо в код.

Во-первых, нужно определить структуру данных графа, поэтому используем это:

class RateGraph(object):
    def __init__(self, rates):
        'Initialize the graph from an iterable of (start, end, rate) tuples.'
        self.graph = {}
        for orig, dest, rate in rates:
            self.add_conversion(orig, dest, rate)

    
    def add_conversion(self, orig, dest, rate):
        'Insert a conversion into the graph.'
        if orig not in self.graph:
            self.graph[orig] = {}
        self.graph[orig][dest] = rate


    def get_neighbors(self, node):
        'Returns an iterable of the nodes neighboring the given node.'
        if node not in self.graph:
            return None
        return self.graph[node].items()
        

    def get_nodes(self):
        'Returns an iterable of all the nodes in the graph.'
        return self.graph.keys()

Затем приступим к работе над DFS. Существует много способов реализации, но на сегодняшний день наиболее распространённым является рекурсивное решение. Начнём с такого:

from collections import deque

def __dfs_helper(rate_graph, node, end, rate_from_origin, visited):
    if node == end:
        return rate_from_origin

    visited.add(node)

    for unit, rate in rate_graph.get_neighbors(node):
        if unit not in visited:
            rate = __dfs_helper(rate_graph, unit, end, rate_from_origin * rate, visited)
            if rate is not None:
                return rate

    return None

def dfs(rate_graph, node, end):
    return __dfs_helper(rate_graph, node, end, 1.0, set())

В двух словах, этот алгоритм начинается с одного узла, перебирает его соседей и немедленно посещает каждого, выполняя рекурсивный вызов функции. Каждый вызов функции в стеке сохраняет состояние своей собственной итерации, поэтому, когда возвращается одно рекурсивное посещение, его родитель немедленно продолжает итерацию. Мы избегаем повторного посещения одного и того же узла, поддерживая набор посещённых узлов во всех вызовах. Мы также вычисляем коэффициент, назначая каждому узлу коэффициент преобразования между ним и источником. Таким образом, когда мы сталкиваемся с целевым узлом/блоком, мы уже создали коэффициент преобразования от исходного узла, и можем просто вернуть его.

Это прекрасная реализация, но она страдает от двух основных недостатков. Во-первых, она рекурсивная. Если окажется, что нужный путь состоит из более тысячи прыжков, мы вылетим со сбоем. Конечно, это маловероятно, но если и есть что-то неприемлемое для долговременного сервиса, так это сбой. Во-вторых, даже если успешно закончим, у ответа некоторые нежелательные свойства.

Я на самом деле уже дал подсказку в начале поста. Вы заметили, как Google показывает коэффициент конверсии 1.0739e-17, но мой расчёт вручную даёт 1.0737e-17? Оказывается, все эти перемножения с плавающей запятой заставляют уже думать о распространении ошибки. Здесь слишком много нюансов для этой статьи, но суть в том, что нужно свести к минимуму умножения с плавающей запятой, чтобы избежать ошибок, которые накапливаются и вызывают проблемы.

DFS — прекрасный алгоритм поиска. Если решение существует, оно его найдёт. Но ему не хватает ключевого свойства: он не обязательно находит самый короткий путь. Для нас это важно, потому что более короткий путь означает меньше прыжков и меньшую ошибку из-за умножений с плавающей запятой. Чтобы решить проблему, мы обращаемся к BFS.

Часть 2. Решение BFS

На этом этапе, если кандидат успешно реализовал рекурсивное решение DFS и остановился на нём, я обычно даю хотя бы слабую рекомендацию по найму этого кандидата. Он понял проблему, выбрал подходящий фрейминг и реализовал рабочее решение. Это наивное решение, поэтому я не настаиваю на его найме, но если он хорошо справился с другими собеседованиями, то не буду рекомендовать отказ.

Это стоит повторить: если сомневаетесь, то напишите наивное решение! Даже если оно не совсем оптимально, наличие кода на доске — уже достижение, и часто на его основе можно найти правильное решение. Скажу иначе: никогда не работайте впустую. Скорее всего, вы подумали о наивном решении, но не хотели его предлагать, потому что знаете, что оно не оптимально. Если вы прямо сейчас готовы выложить лучшее решение, это прекрасно, но если нет, то зафиксируйте достигнутый прогресс, прежде чем переходить к более сложным вещам.

С этого момента поговорим об улучшениях алгоритма. Основные недостатки рекурсивного решения DFS заключаются в том, что оно рекурсивно и не минимизирует количество умножений. Как мы скоро увидим, BFS минимизирует количество умножений, и его тоже очень сложно реализовать рекурсивно. К сожалению, нам придётся отказаться от рекурсивного решения DFA, поскольку для его улучшения потребуется полностью переписать код.

Без дальнейших церемоний, представляю итеративный подход на основе BFS:

from collections import deque

def bfs(rate_graph, start, end):
    to_visit = deque()
    to_visit.appendleft( (start, 1.0) )
    visited = set()

    while to_visit:
        node, rate_from_origin = to_visit.pop()
        if node == end:
            return rate_from_origin
        visited.add(node)
        for unit, rate in rate_graph.get_neighbors(node):
            if unit not in visited:
                to_visit.appendleft((unit, rate_from_origin * rate))

    return None

Эта реализация функционально сильно отличается от предыдущей, но если внимательно посмотреть, она делает примерно то же самое, с одним существенным изменением: в то время как рекурсивный DFS сохраняет состояние дальнейшего маршрута в стеке вызовов, эффективно реализуя стек LIFO, итеративное решение сохраняет его в очереди FIFO.

Отсюда вытекает свойство «кратчайший путь / наименьшее число умножений». Мы посещаем узлы в том порядке, в котором они встречаются, и таким образом получаем поколения узлов. Первый узел вставляет своих соседей, а затем мы посещаем этих соседей по порядку, всё время прикрепляя их соседей и так далее. Свойство кратчайшего пути вытекает из того, что узлы посещаются в порядке их расстояния от источника. Поэтому, когда мы сталкиваемся с местом назначения, мы знаем, что нет более раннего поколения, которое могло бы к нему привести.

В этот момент мы почти закончили. Сначала нужно ответить на несколько вопросов, и они заставляются вернуться к первоначальной постановке проблемы.

Во-первых, самое тривиальное, что делать, если исходная единица измерения не существует? То есть мы не можем найти узел с заданным именем. На практике нужно выполнить некоторую нормализацию строк, чтобы Фунт, ФУНТ и lb указывали на один узел «фунт» (или какое-то другое каноническое представление), но это выходит за рамки нашего вопроса.

Во-вторых, что делать, если между двумя единицами нет преобразования? Напомним, что в исходных данных только преобразования между единицами, и оно не даёт никаких указаний на то, можно ли получить из одной конкретной единицы другую. Это сводится к тому, что преобразования и пути прямо эквивалентны, поэтому если между двумя узлами нет пути, то нет преобразования. На практике вы в конечном итоге получаете несвязанные острова единиц измерения: один для расстояний, один для весов, один для валют и т. д.

Наконец, если внимательно посмотреть на граф выше, оказывается, что вы не можете произвести конверсию между хэндами и световыми годами с таким решением. Направление связей между узлами означает, что от хэнда к световым годам нет пути. Впрочем, это довольно легко исправить, потому что преобразования можно обратить в другую сторону. Мы можем изменить наш код инициализации графа следующим образом:

def add_conversion(self, orig, dest, rate):
    'Insert a conversion into the graph. Note we insert its inverse also.'
    if orig not in self.graph:
        self.graph[orig] = {}
    self.graph[orig][dest] = rate

    if dest not in self.graph:
        self.graph[dest] = {}
    self.graph[dest][orig] = 1.0 / rate

Часть 3. Оценка

Готово! Если кандидат дошёл до этого момента, то я с большой вероятностью буду рекомендовать его к найму. Если вы изучали информатику или прошли курс алгоритмов, то можете спросить: «И этого действительно достаточно, чтобы пройти собеседование у этого парня?», на что я отвечу: «По сути, да».

Прежде чем вы решите, что вопрос слишком простой, давайте рассмотрим, что должен сделать кандидат, чтобы достичь этой точки:

• Понять вопрос
• Построить сеть преобразований в виде графа
• Понять, что коэффициенты можно сопоставить с рёбрами графа
• Увидеть возможность использования алгоритмы поиска для достижения этой цели
• Выбрать свой любимый алгоритм и изменить его, чтобы отслеживать коэффициенты
• Если он реализовал DFS как наивное решение, осознать его слабые стороны
• Реализовать BFS
• Отступить назад и изучить крайние случаи:
  • Что, если нас cпросят о несуществующем узле?
  • Что делать, если коэффициент преобразования не существует?
• Осознать, что обратные преобразования возможны и, вероятно, необходимы

Этот вопрос легче предыдущих, но при этом так же труден. Как и во всех предыдущих вопросах, кандидат должен совершить мысленный прыжок от абстрактно сформулированного вопроса к алгоритму или структуре данных, которая открывает путь к решению. Единственное, что здесь итоговый алгоритм менее продвинутый, чем в других вопросах. Вне этого алгоритмического материала действуют те же требования, особенно в отношении крайних случаев и корректности.

«Но подождите!, — вы можете спросить. — Разве Google не одержима сложностью рантайма? Вы даже не спросили о временной или пространственной сложности этой проблемы. Да ну!» Вы также можете спросить: «Погодите, вы же давали оценку "настоятельно рекомендую к найму"? Как её получить?» Очень хорошие вопросы, оба. Это приводит нас к нашему заключительному дополнительному бонусному раунду…

Часть 4. Можно ли сделать лучше?

В этот момент я хотел бы поздравить кандидата с хорошим ответом и дать понять, что всё дальнейшее — просто бонус. Когда давление исчезнет, мы сможем начать творить.

Итак, какова сложность выполнения BFS? В худшем случае мы должны рассмотреть каждый отдельный узел и ребро, что даёт линейную сложность O(N+E). Это поверх такой же сложности O(N+E) построения графа. Для поисковой системы это, вероятно, хорошо: тысячи единиц измерения достаточно для большинства разумных приложений, а выполнение поиска в памяти по каждому запросу не является чрезмерной нагрузкой.

Тем не менее, можно сделать лучше. Для мотивации рассмотрим, как этот код вставляется в поисковую строку. Преобразования некоторых нестандартных единиц встречаются чуть чаще, поэтому мы будем вычислять их снова и снова. Каждый раз выполняется поиск, вычисляются промежуточные значения и т. д.

Часто предлагают просто кэшировать результаты вычисления. Всякий раз, когда вычисляется преобразование единиц, мы всегда можем просто добавить ребро между двумя преобразованиями. В качестве бонуса, мы получим обратное преобразование, причём бесплатно! Готово?

Действительно, это даст нам асимптотически постоянное время поиска, но будет стоить хранения дополнительных рёбер. Это на самом деле становится довольно дорогим: со временем мы будем стремиться к полному графу, поскольку все пары преобразований постепенно вычисляются и сохраняются. Число возможных рёбер в графе составляет половину квадрата числа узлов, поэтому для тысячи узлов нам понадобится полмиллиона рёбер. Для десяти тысяч узлов — около пятидесяти миллионов и т. д.

Выходя за рамки поисковой системы, для графа из миллиона узлов мы стремимся к половине триллиона рёбер. Такое количество просто неразумно хранить, плюс мы тратим время на вставку рёбер в граф. Мы должны сделать лучше.

К счастью, есть способ добиться постоянного времени для поиска коэффициентов, без квадратичного роста пространства. На самом деле, почти всё необходимое уже у нас прямо под носом.

Часть 4. Постоянное время

Итак, тотальное кэширование на самом деле близко к оптимальному решению. В этом подходе мы (в конечном итоге) получаем рёбра между всеми узлами, то есть наше преобразование сводится к поиску одного ребра. Но действительно ли нужно хранить преобразования из каждого узла в каждый узел? Что, если мы просто сохраним коэффициенты преобразования от одного узла ко всем остальным?

Взглянем ещё раз на решение BFS:

from collections import deque

def bfs(rate_graph, start, end):
    to_visit = deque()
    to_visit.appendleft( (start, 1.0) )
    visited = set()

    while to_visit:
        node, rate_from_origin = to_visit.pop()
        if node == end:
            return rate_from_origin
        visited.add(node)
        for unit, rate in rate_graph.get_neighbors(node):
            if unit not in visited:
                to_visit.appendleft((unit, rate_from_origin * rate))

    return None

Посмотрим, что здесь происходит: мы начинаем с исходного узла, и для каждого узла, с которым сталкиваемся, вычисляем коэффициент преобразования от источника к этому узлу. Затем, как только прибываем в пункт назначения, мы возвращаем коэффициент между исходным и конечным пунктами и отбрасываем промежуточные коэффициенты.

Эти промежуточные коэффициенты являются ключевыми. А что, если мы их не выбросим? А что, если вместо этого мы их запишем? Все самые сложные и непонятные поиски становятся простыми: чтобы найти отношение A к B, сначала найдём отношение X к B, затем разделим его на отношение X к A, и всё готово! Визуально это выглядит так:

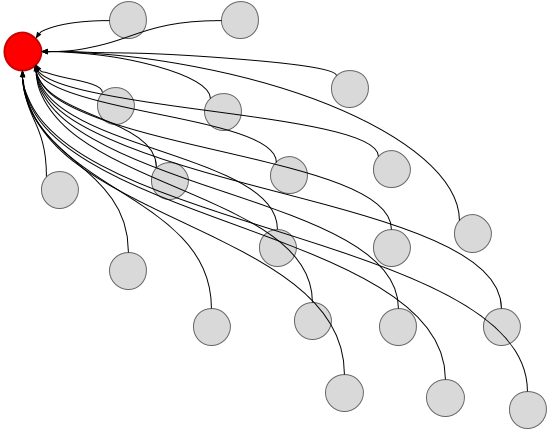
Обратите внимание, что между любыми двумя узлами не больше двух рёбер

Оказывается, для вычисления этой таблицы нам почти не нужно изменять решение BFS:

from collections import deque

def make_conversions(graph):
    def conversions_bfs(rate_graph, start, conversions):
        to_visit = deque()
        to_visit.appendleft( (start, 1.0) )

        while to_visit:
            node, rate_from_origin = to_visit.pop()
            conversions[node] = (start, rate_from_origin)
            for unit, rate in rate_graph.get_neighbors(node):
                if unit not in conversions:
                    to_visit.append((unit, rate_from_origin * rate))

        return conversions

    conversions = {}
    for node in graph.get_nodes():
        if node not in conversions:
            conversions_bfs(graph, node, conversions)
    return conversions

Структура преобразований представлена словарём единицы A в двух значениях: корень для связанного компонента единицы A и коэффициент преобразования между корневой единицей и единицей A. Поскольку мы вставляем единицу в этот словарь при каждом посещении, то можем использовать пространство ключей этого словаря в качестве набора посещений вместо использования выделенного набора посещений. Обратите внимание, что у нас нет конечного узла, и вместо этого мы перебираем узлы, пока не закончим.

За пределами этого BFS есть вспомогательная функция, которая перебирает узлы в графе. Всякий раз, когда она сталкивается с узлом вне словаря преобразования, то запускает BFS, начиная с этого узла. Таким образом, мы гарантированно свернём все узлы в их связанные компоненты.

Когда нужно найти соотношение между единицами, мы просто используем структуру преобразований, которую только что вычислили:

def convert(conversions, start, end):
    'Given a conversion structure, performs a constant-time conversion'
    try:
        start_root, start_rate = conversions[start]
        end_root, end_rate = conversions[end]
    except KeyError:
        return None

    if start_root != end_root:
        return None

    return end_rate / start_rate

Ситуация «нет такой единицы» обрабатывается прослушиванием исключения при доступе к структуре преобразований. Ситуация «нет таких преобразований» обрабатывается сравнением корней двух величин: если у них разные корни, значит, они обнаружены через два разных вызова BFS, то есть находятся в двух разных связанных компонентах, и поэтому никакого пути между ними не существует. Наконец, мы выполняем преобразование.

Вот так! У нынешнего решения при предварительной обработке сложность O(V+E) (не хуже, чем у предыдущих решений), но она также ищет с постоянным временем. Теоретически, мы удваиваем требования к пространству, но бóльшую часть времени нам больше не нужен исходный граф, поэтому мы можем просто удалить его и использовать только этот. При этом пространственная сложность на самом деле меньше, чем исходный граф: тот требует O(V+E), потому что должен хранить все рёбра и вершины, а эта структура требует только O(V), потому что нам больше не нужны рёбра.

Результаты

Если вы продвинулись так далеко, то можете вспомнить, что изначально один из вопросов был в том, чтобы проверить, сможет ли более простая проблема по-прежнему оставаться полезной в выборе достойных кандидатов и может ли она дать лучшую картину способностей. Я хотел бы дать какой-то окончательный научный ответ, но у меня есть только истории из личного опыта. Тем не менее, я заметил некоторые положительные результаты.

Если разбить решение этой задачи на четыре препятствия (обсуждение фрейминга, выбор алгоритма, реализация, обсуждение выполнения за постоянное время), то к концу собеседования почти все кандидаты дошли до «выбора алгоритма». Как я и подозревал, обсуждение фрейминга стало хорошим фильтром: кандидаты либо сразу выводили граф, либо никак не могли к нему прийти, несмотря на существенные подсказки.

Это уже сразу полезный сигнал. Я могу понять, когда человек не знает продвинутых или неясных структур данных, потому что будем честными, вам нечасто придётся реализовывать непересекающиеся множества. Но графы — фундаментальная структура данных и преподаётся в рамках практически любого вводного курса по этой теме. Если кандидат изо всех сил пытается понять их или не может их легко применить, вероятно, ему будет трудно добиться успеха в Google (по крайней мере, в моё время там, не знаю как сегодня).

С другой стороны, выбор алгоритма оказался не особенно полезным источником сигнала. Люди, которые прошли стадию фрейминга, обычно без особых проблем добирались до алгоритма. Подозреваю, это связано с тем, что алгоритмы поиска почти всегда преподаются вместе с самими графами, поэтому, если кто-то знаком с одним, то знает и другое.

Реализация оказалась непростой. У многих людей не было проблем с рекурсивной реализацией DFS, но, как я уже упоминал выше, эта реализация не подходит для продакшна. К моему удивлению, итеративные реализации BFS и DFS, похоже, не очень знакомы людям, и даже после явных подсказок они часто плавали в теме.

В моём представлении любой, кто прошёл этап реализации, уже заслужил от меня рекомендацию «Нанимать», а этап обсуждения постоянного времени выполнения просто бонусный. Хотя в статье мы подробно рассмотрели решение, на практике обычно более продуктивным является устное обсуждение, а не написание кода. Очень немногие кандидаты сразу могли высказать решение. Мне часто приходилось давать существенные подсказки, и даже тогда многие люди не могли его найти. Это нормально: как и предполагалось, рейтинг «настоятельно рекомендую» трудно заслужить.

Но подождите, это ещё не всё!

В основном, мы рассмотрели проблему целиком, но если вы заинтересованы в её дальнейшем изучении, то есть целый ряд расширений, в которые я не буду погружаться. Оставляю следующие упражнения для читателя:

Во-первых, разминка: в решении для постоянного времени, которое я выложил, я произвольно выбрал корневой узел каждого подключённого компонента. В частности, я использую первый узел компонента, с которым мы сталкиваемся. Это не оптимально, потому что для всех известных значений мы выбрали какой-то узел на краю графа, в то время как какой-то другой узел может быть ближе к центру с более короткими путями ко всем другим узлам. Ваша задача состоит в том, чтобы заменить этот произвольный выбор на тот, который минимизирует количество требуемых умножений и минимизирует распространение ошибки с плавающей запятой.

Во-вторых, во всех рассуждениях предполагалось, что все равные пути через граф равны изначально, что не всегда так. Один из интересных вариантов этой проблемы — конвертация валют: узлы — это валюты, а рёбра от A до B и наоборот — это цены на предложение/спрос каждой валютной пары. Мы можем перефразировать вопрос о конверсии единиц как вопрос о валютном арбитраже: реализовать алгоритм, который, учитывая график конвертации валюты, вычисляет через график цикл, который даст трейдеру больше денег, чем начальная сумма. Не учитывайте никаких комиссий за транзакции.

Наконец, настоящая жемчужина: некоторые единицы выражаются в виде комбинации различных базовых единиц. Например, ватт определяется в системе СИ как кг•м²/с³. Последняя задача заключается в расширении этой системы для поддержки преобразования между этими единицами, учитывая только определения основных единиц СИ.

Если у вас есть вопросы, не стесняйтесь обращаться ко мне на reddit.

Заключение

Когда я начал задавать эту задачу на собеседованиях, то надеялся, что она будет немного легче предыдущих. Эксперимент был в значительной степени успешным: если кандидат сразу видел решение, то обычно быстро справлялся с задачей, так что у нас оставалось много времени, чтобы поговорить о продвинутом решении с постоянным временем. Люди, которые испытывали затруднения, как правило, спотыкались в местах, отличных от алгоритмического концептуального скачка: кандидат не мог подходящим способом полностью сформулировать проблему или набросал хорошее решение, но не смог перевести его в рабочий код. Независимо от того, где и когда они испытывали затруднения, я обнаружил, что могу получить значимую информацию о сильных и слабых сторонах кандидатов.

Надеюсь, вы нашли полезной эту статью. Понимаю, что здесь может быть не так много приключений с алгоритмами, как в некоторых предыдущих статьях. На собеседованиях разработчиков принято обильно обсуждать алгоритмы. Но правда в том, что значительные сложности возникают при использовании даже простого, хорошо известного метода. Весь код — в репозитории этого цикла статей.

Автор: m1rko

Источник