Пролог
Существует классическая задача:
Каждый гость на встрече обменивается рукопожатием с другим. Всего было 78 рукопожатий. Сколько гостей пришло на встречу?
Эта задача представляет интерес только лишь потому, что её нынче задают при трудоустройстве на работу. Поэтому надо уметь её решить и главное доходчиво объяснить решение.
Определения
Для начала микро ликбез.
Граф - множество вершин и рёбер (палочки и кружочки).
Неориентированный граф — это граф, рёбра которого не имеют направления. Это значит, что соединение между двумя вершинами можно пройти в обе стороны. Проще говоря палочки без стрелок.
Две вершины неориентированного графа смежны, если они являются разными концами одного ребра
полный граф - простой неориентированный граф, в котором каждая пара различных вершин смежна.

Сочетание - неупорядоченная выборка из n элементов по k без повторений. Вычисляется по кнопке калькулятора nCr.
Это всё, что надо для решения этой задачи.
Решение
Это задача из раздела дискретной математики, комбинаторики и алгебры.
Если людей принять за вершины графа, а рукопожатия за ребра графа, то сформируется так называемый полный граф. Как математически связаны количество ребер и количеcтво вершин?
Занумеруем всех гостей натуральными числами (1; 2; 3; 4; 5 и т д). Для одного рукопожатия надо выбрать два гостя. Рукопожатие это неупорядоченная (если Уолли жмет руку Ашоку, то и Ашок жмет руку Уолли) выборка без повторений (Тэд же не может пожать руку сам себе).

Согласно формуле nСm надо посчитать
Вот и получается, что у полного графа есть свойство. Если n- это количество вершин, то
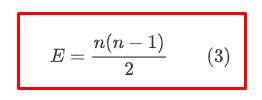
(3) это количество рёбер. Задача сводится к тому, что надо решить уравнение (4)
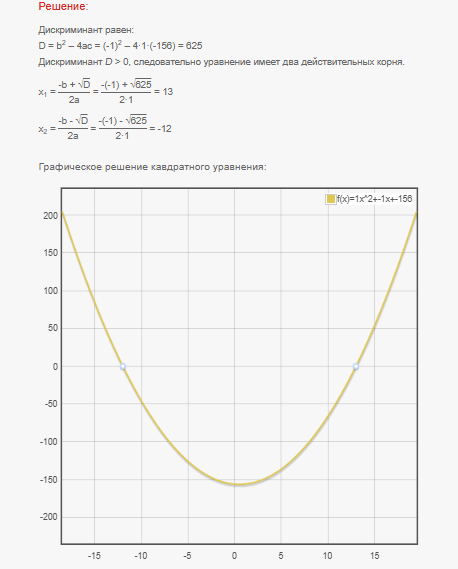
Это уравнение вырождается в квадратное уравнение
Так как ответ мы ищем в множестве натуральных чисел, то выбираем решение 13. Ответ: на встрече пришло 13 человек.
Итог
Вот теперь и Вы умеете решать задачу про рукопожатия и можете объяснить другим.
Ссылки
|
# |
Название |
URL |
|
1 |
Полный Граф |
|
|
3 |
Рукопожатия |
https://tproger.ru/articles/7-zakovyristyh-logiko-matematicheskih-zadach |
|
2 |
||
|
4 |
Калькулятор квадратных уравнений |
Автор: aabzel




