Метод конечных элементов своими руками

Метод конечных элементов (МКЭ) применяют в задачах упругости, теплопередачи, гидродинамики — всюду, где нужно как-то дискретизировать уравнения сплошной среды или поля. На Хабре было множество статей с красивыми картинками о том, в каких отраслях и с помощью каких программ этот метод приносит пользу. Однако мало кто пытался объяснить МКЭ от самых основ, с простенькой учебной реализацией, желательно без упоминания частных производных через каждое слово.

Мы напишем МКЭ для расчёта упругой двумерной пластины на прочность и жёсткость. Код займёт 1200 строк. Туда войдёт всё: интерактивный редактор, разбиение модели на треугольные элементы, вычисление напряжений и деформаций, визуализация результата. Ни одна часть алгоритма не спрячется от нас в недрах MATLAB или NumPy. Код будет ужасно неоптимальным, но максимально ясным.

Размышление над задачей и написание кода заняли у меня неделю. Будь у меня перед глазами такая статья, как эта, — справился бы быстрее. У меня её не было. Зато теперь она есть у вас.

Редактор

Интерактивный редактор с GUI сам по себе не имеет никакого отношения к МКЭ. Однако полезно начать разговор именно с него, поскольку его возможности должны один в один соответствовать тем входным данным, которые мы скормим МКЭ и которые будут минимально достаточны для получения хоть какого-то наглядного результата:

1. Ввод границы пластины в виде одного многоугольника (вообще говоря, невыпуклого, но без самопересечений).

2. Ввод отверстий в пластине в виде многоугольников. Круглых отверстий у нас не будет.

3. Ввод дополнительных точек пластины, которые будут участвовать в разбиении на треугольники.

4. Ввод связей (шарнирных закреплений) в любой точке пластины. У нас любой шарнир будет фиксировать точку сразу по обеим координатам.

5. Ввод внешних сил, прикладываемых к любой точке пластины, в виде двух компонент. Внешних моментов и распределённых нагрузок у нас не будет.

6. Ввод свойств материала: модуля Юнга, коэффициента Пуассона, предельно допустимого напряжения. Туда же отнесём и толщину пластины.

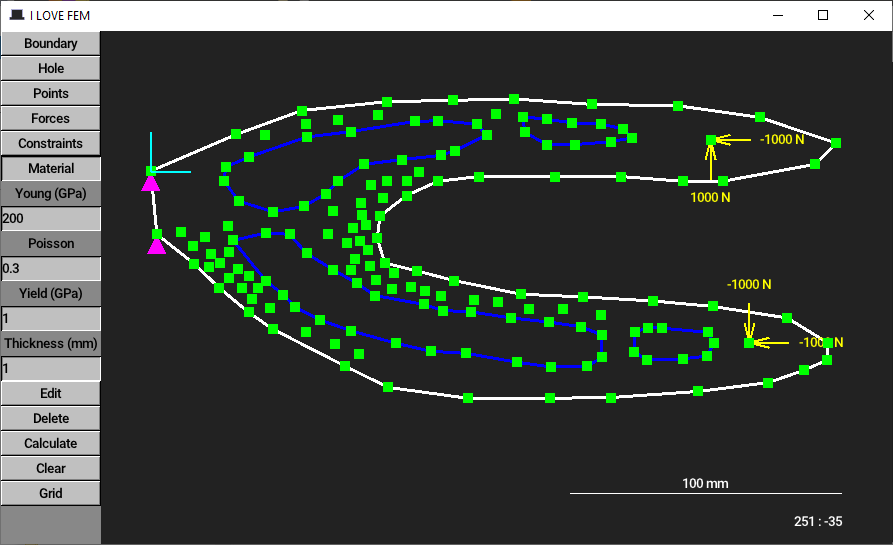
С точки зрения дальнейшего расчёта, внешняя граница пластины ничем не отличается от отверстий, кроме направления обхода вершин: внешняя граница обходится против часовой стрелки, границы отверстий — по часовой. Если пользователь ввёл наоборот, редактор сам выворачивает введённую ломаную. Для определения имеющегося направления обхода есть очень простой и изящный метод.

Шарниров должно быть как минимум два — иначе вся пластина будет кинематически подвижна, а расчёт на прочность и жёсткость требует статики. Перемещения точек могут происходить только в результате упругой деформации.

Разбиение на треугольники

Эта часть — подготовительная, но самая трудоёмкая. В ней чистая геометрия и ещё никакой механики.

Триангуляция набора точек

Любой заданный набор точек (вершин границ и дополнительных точек) можно соединить отрезками многими разными способами. Мы построим триангуляцию Делоне. Это ещё не какой-то определённый алгоритм соединения точек в треугольники, а лишь желаемое свойство результата: внутри описанной окружности любого треугольника не должно быть вершин никаких других треугольников. Это свойство очень удобно, поскольку предотвращает появление слишком длинных и узких треугольников.

Для триангуляции Делоне возьмём алгоритм Боуера-Уотсона:

1. Построим фальшивый супер-треугольник, достаточно большой, чтобы внутрь него заведомо попали все наши точки.

2. Будем добавлять точки по одной.

3. Каждая новая точка, вообще говоря, портит несколько треугольников — в том смысле, что для них перестаёт выполняться условие Делоне: новая точка попадает внутрь их описанных окружностей. Соберём множество испорченных треугольников.

4. Испорченные новой точкой треугольники геометрически образуют некий многоугольник (вообще говоря, невыпуклый). Найдём его границу. Она состоит из всех тех сторон испорченных треугольников, которые принадлежат только одному, а не двум испорченным треугольникам.

5. Перетриангулируем испорченный многоугольник. Для этого удалим все испорченные треугольники и соединим новую точку со всеми вершинами границы. Поскольку многоугольник невыпуклый, такой способ может дать неправильные (перекрывающиеся) треугольники, однако это автоматически исправится на следующей итерации цикла по точкам. Но сразу позаботимся о том, чтобы у всех новых треугольников было правильное направление обхода — против часовой стрелки.

6. Когда цикл по точкам завершён, удалим остатки супер-треугольника.

Добавление отрезков

Коварство всех алгоритмов триангуляции Делоне состоит в том, что входными данными для них служат наборы точек, и строится фактически триангуляция выпуклой оболочки этих точек. Алгоритмы ничего не знают про нужные нам отрезки границ пластины. Часто эти отрезки сами собой появляются в итоговой триангуляции, но могут и не появиться — никаких гарантий тут нет. Такие отрезки приходится добавлять вручную (отчего, конечно, триангуляция перестаёт быть честной Делоне). Для этого возьмём кусочек алгоритма Слоуна, который расчищает место под новый отрезок:

1. Найдём все отрезки границ, которых не оказалось в триангуляции Делоне.

2. Будем добавлять эти отрезки по одному.

3. Для каждого такого отрезка найдём все стороны треугольников, с которыми он пересекается. Если пересечений нет, всё хорошо, выходим из цикла.

4. Любая пересекающаяся сторона треугольника является диагональю какого-то четырёхугольника, составленного из двух смежных треугольников. Найдём вторую диагональ этого четырёхугольника.

5. Если четырёхугольник оказался выпуклым, то перетриангулируем его, заменив одну диагональ другой. Здесь мы надеемся на то, что если одна диагональ пересекалась с новым отрезком, то другая не будет. Может быть, нам повезёт. (Если четырёхугольник невыпуклый, то так сделать точно нельзя, потому что вторая диагональ пройдёт вне его и зацепит другие треугольники).

Итак, мы испортили Делоне, зато силой впихнули нужный нам отрезок:

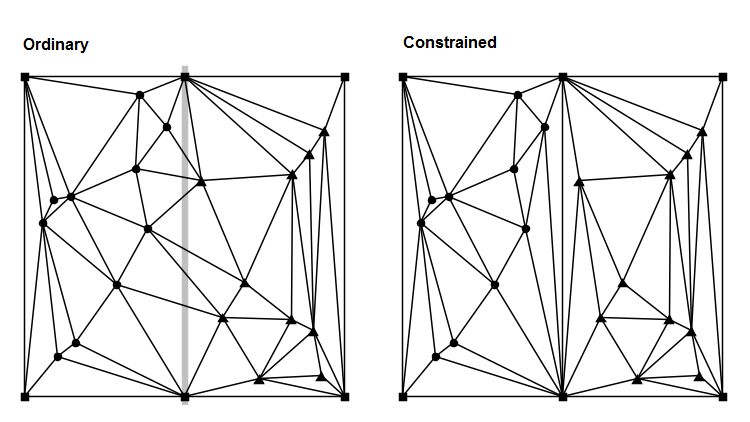
Отрезание лишнего

Теперь осталось убрать все треугольники, лежащие вне заданных границ пластины.

1. Для всех треугольников построим множества смежных треугольников — его соседей.

2. Найдём какой-нибудь треугольник, примыкающий к границе извне. Это означает, что какая-то его сторона совпадает с каким-то отрезком границы, но обходится в противоположную сторону. Если таких нет, задача решена.

3. Рекурсивно удалим этот треугольник и всех его соседей, до которых можно добраться, не пересекая заданных границ.

Готово. Можно приступать к МКЭ как таковому.

Прочность и жёсткость

Философия МКЭ

Метод неспроста назван методом конечных (не бесконечно малых) элементов. Наш треугольный элемент может быть весьма большим. При этом интересующие нас величины — упругие перемещения внутренних точек треугольника — как-то интерполируются по его площади, если известны перемещения его вершин. В этом и заключается дискретизация задачи: у нас было бесконечно много неизвестных перемещений всех точек пластины, а остались в качестве неизвестных только перемещения вершин — тех точек, которые мы соединяли в треугольники. Если нужны перемещения промежуточных точек — можем найти их из закона интерполяции.

Беда любых расчётов в статике и сопромате — учёт связей (шарниров, заделок) через неизвестные силы реакций в них. Про эти силы известно только то, что в совокупности со всеми остальными силами они должны давать нулевые перемещения закреплённых точек. Эти силы приходится искать из уравнений. Ещё хуже то, что системы в сопромате, как правило, статически неопределимые — то есть из одних только условий равновесия невозможно найти силы реакций. МКЭ борется с этой проблемой в зародыше: вместо перемещений точек он вводит перемещения степеней свободы. Если точка закреплена — у неё нет степеней свободы, нет новых неизвестных перемещений, нет и уравнений для них. Такие точки попросту вычёркиваются из рассмотрения. (Замечание для продвинутых любителей механики: этот трюк со степенями свободы немного напоминает то, что делает подход Лагранжа в аналитической динамике.)

Треугольный элемент

Геометрический треугольник — это ещё не элемент, пригодный для расчёта. Сперва его нужно наделить механическими свойствами. Если мы взялись говорить о степенях свободы, то у свободного деформируемого треугольника на плоскости их будет шесть: по два независимых перемещения q у каждой из вершин. Независимых воздействий (сил) F — тоже шесть:

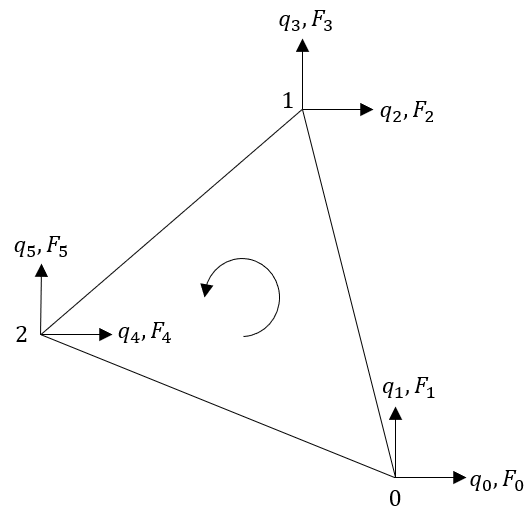
Если теперь использовать гипотезу линейности свойств материала (упругие перемещения пропорциональны силам), то связь перемещений с силами можно представить некоей матрицей k размера 6×6 — матрицей жёсткости элемента:

Можно воспринимать эту запись как своего рода многомерный аналог закона Гука для пружины kq = F. Конкретная формула для матрицы жёсткости немного громоздка, но её можно подсмотреть у меня в коде либо в замечательном конспекте лекции, где она дана с выводом (раздел 4.7, пункт 2). Для нас сейчас важно то, что матрица жёсткости элемента полностью выражается через координаты его вершин и свойства материала, поэтому её можно вычислить индивидуально для каждого элемента, пренебрегая пока соединением элементов друг с другом.

Треугольник вместе со своей матрицей жёсткости — это и есть наш конечный элемент. В том виде, как мы его задали, он реализует самый простой — линейный закон интерполяции перемещений между вершинами.

Соединение элементов

Количество степеней свободы всей пластины (без учёта связей) в двумерном случае равно удвоенному количеству точек триангуляции N, что, конечно, меньше суммы степеней свободы всех треугольников в отдельности. Этим и выражается тот факт, что треугольники на самом деле соединены и перемещения их общих вершин не могут быть независимыми. Первое, что нам нужно, чтобы учесть соединение элементов, — это уметь преобразовывать номер степени свободы элемента (от 0 до 5) в номер степени свободы всей пластины (от 0 до 2N — 1).

Теперь можно составить глобальную матрицу жёсткости K, связывающую упругие перемещения степеней свободы пластины с внешними силами, действующими на пластину:

Если известно, что для какого-то элемента степень свободы i соответствует глобальной степени свободы m, а степень свободы j — глобальной степени свободы n, то член матрицы k добавляется к соответствующему члену матрицы K:

Так из жёсткостей отдельных элементов набирается глобальная матрица жёсткостей.

Следующий шаг — учёт связей. Как и было обещано, в МКЭ это удивительно простая операция. Если на глобальную степень свободы m наложена связь (перемещения по ней запрещены), то из матрицы K просто вычёркивается m-я строка и m-й столбец. В итоге остаётся матрица K' меньшего размера, причём если K была вырожденной (не позволяла выразить q через F), то K' уже не вырождена.

Перемещения

Предположим, что r степеней свободы мы вычеркнули. Остаётся решить систему уравнений относительно оставшихся неизвестных упругих перемещений:

Здесь мы записали решение формально, через обратную матрицу, по аналогии с тем, как сделали бы со скалярным законом Гука: q = F / K. Но на практике вовсе необязательно обращать матрицу. Можно взять что-нибудь попроще и понаивнее, вроде метода Гаусса.

Теперь вспомним, каким точкам соответствовали невычеркнутые степени свободы — и всё. Перемещения точек мы нашли и тем самым узнали, как деформирована пластина. Можно сделать в редакторе опциональный режим отображения пластины с деформацией, в котором к исходным координатам всех точек прибавляются их перемещения.

Напряжения

Линейное нарастание перемещения от точки к точке в пределах каждого элемента означает постоянство относительной деформации, а оно, в свою очередь, означает постоянство напряжения по всей площади элемента. Вычислить это напряжение можно, пользуясь теми же величинами, что и при расчёте матрицы жёсткости элемента, плюс найденными перемещениями вершин. За формулами вновь отсылаю либо к своему коду, либо к конспекту лекции (раздел 4.8).

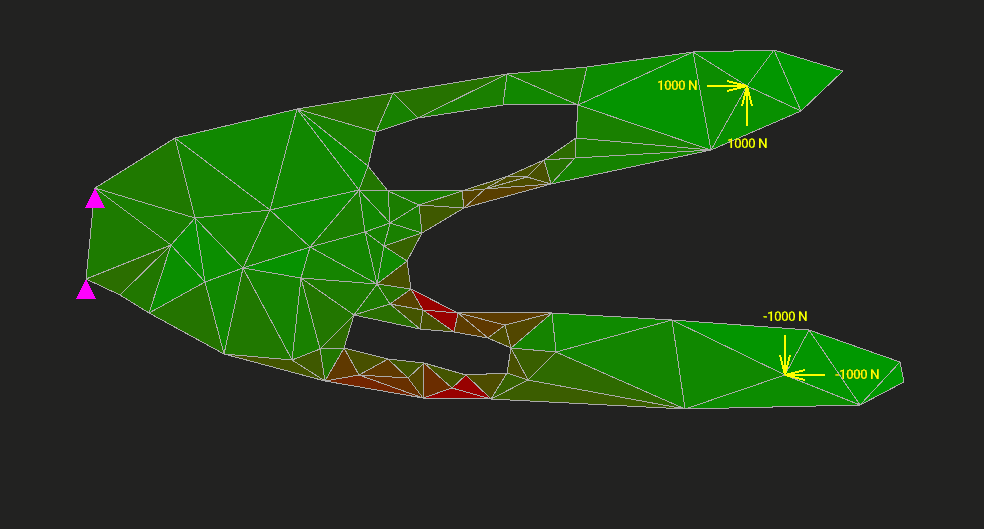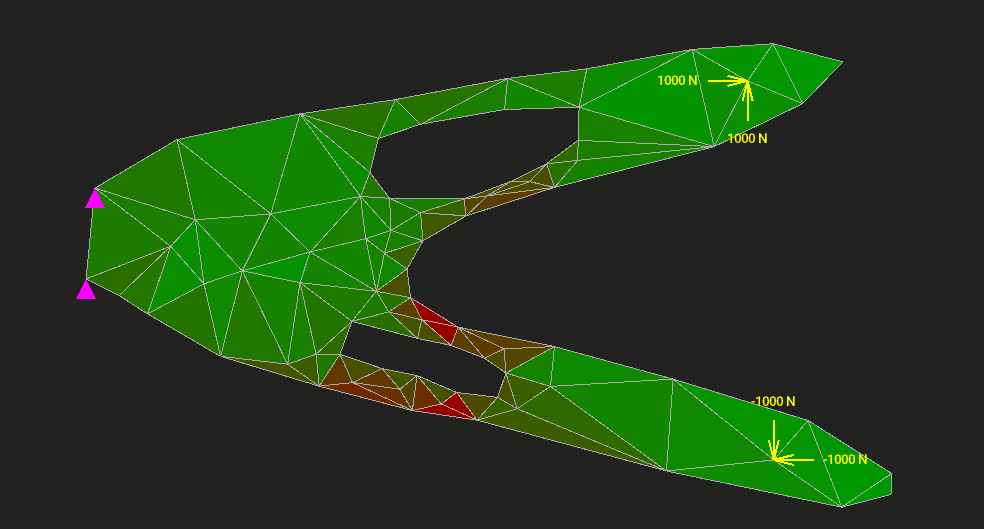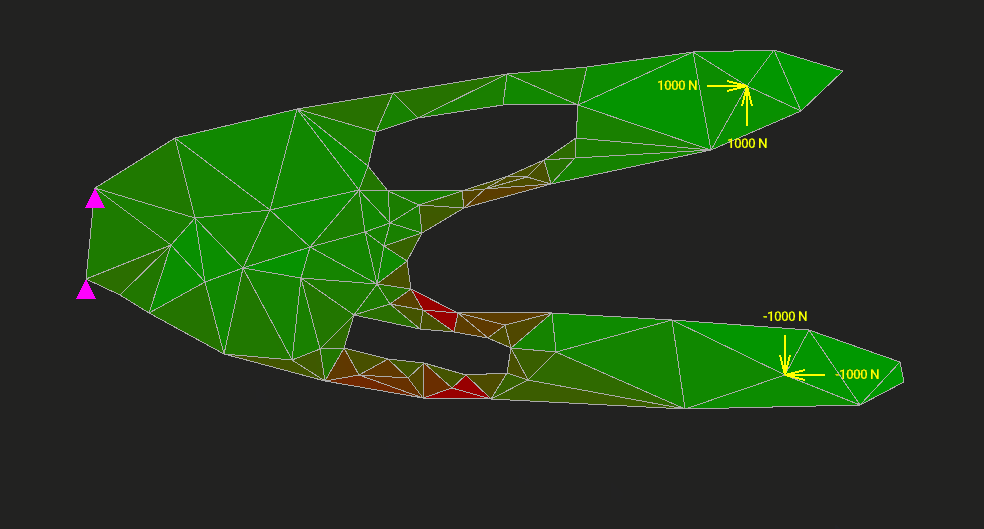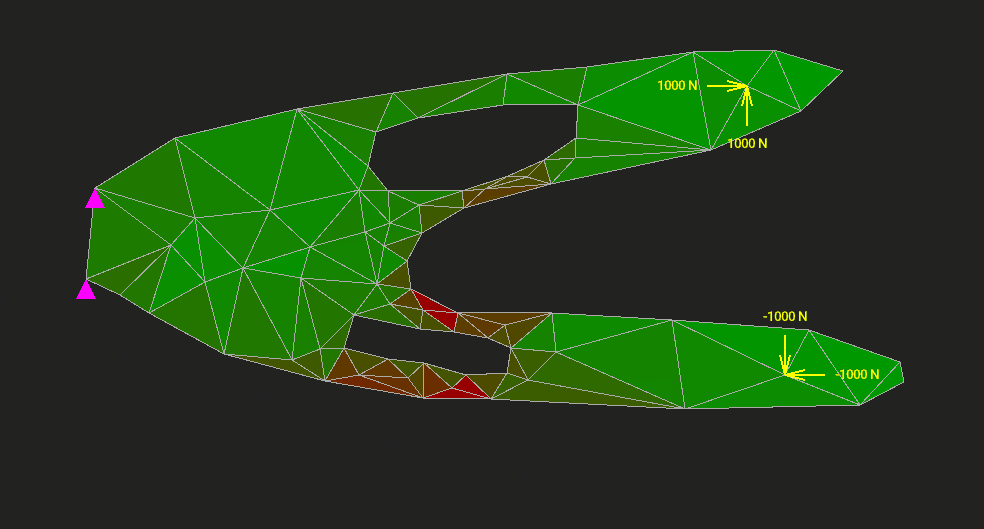
Здесь возникает трудность. Поскольку наша задача двумерная, то напряжений оказывается не одно, а целых три: напряжение растяжения по оси x, растяжения по оси y и сдвига. Все их можно найти, но возникает вопрос: какому одному напряжению растяжения эквивалентны эти три? Эквивалентность здесь нужно понимать в смысле равноопасности. Конкретных количественных критериев эквивалентности существует много. Мы возьмём самый распространённый критерий Мизеса. Это эквивалентное напряжение покажет нам, насколько материал близок к переходу упругой деформации в необратимую пластическую. В соответствии с этим напряжением мы и раскрасим треугольный элемент в редакторе.

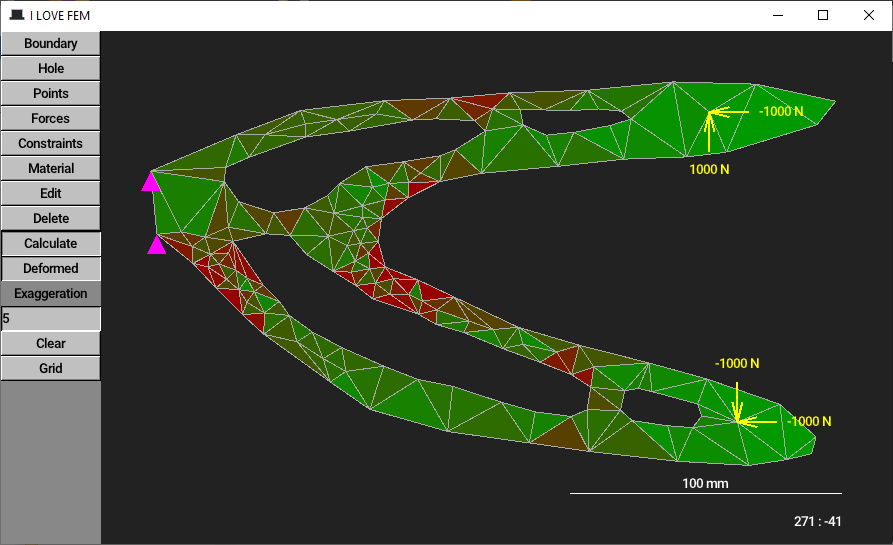
Проверка

Теперь, когда основная задача решена, устроим небольшую проверку и нашему методу, и нашей интуиции. Как изгибается балка под действием силы? Обычно к такой простой задаче из базового курса сопромата не применяют МКЭ. А мы применим:

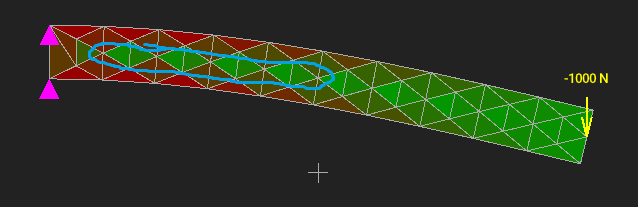
И сразу увидим интересное: какой бы ни была нагрузка, элементы вблизи продольной оси балки (обведены голубым) остаются ненапряжёнными. На самом деле, это логично: слои материала сверху от продольной оси балки испытывают растяжение, снизу от оси — сжатие. Значит, где-то между ними должны быть слои, не испытывающие ни того, ни другого. Ну точно картинка из учебника, только перевёрнутая:

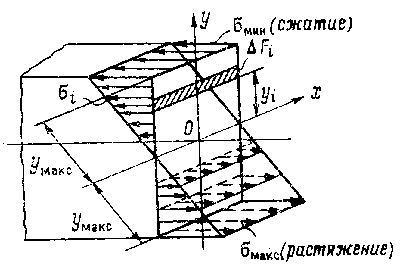
Замечания о реализации

Исходный код программы написан на моём скриптовом языке Umka с использованием игрового фреймворка Tophat. В принципе, вы можете смело проигнорировать моё запоздалое признание. Во всяком случае, надеюсь, что синтаксис языка оказался достаточно прозрачен, чтобы любой человек, видевший C, JavaScript и тем более Go, без труда прочёл написанное.

Для меня было важно, что проект стал первым неигровым применением Tophat. Возможности фреймворка по созданию кросс-платформенного GUI оказались очень полезны для интерактивного редактора. Высокоуровневые типы данных Umka — динамические массивы и словари — отлично послужили в вычислениях. Чувствовалась некоторая нехватка встроенных перечислений и множеств (последние я имитировал словарями). Быстродействие, конечно, оставляло желать лучшего, да и вообще, что может быть абсурднее, чем писать тяжёлые расчётные алгоритмы на интерпретируемом языке без JIT? Но для прототипирования этого вполне хватило, и те модели, которые вы видите на скриншотах, рассчитывались не более нескольких секунд.