Главная

Почему векторное произведение существует только в R^0, R^1, R^3, R^7?

2025-08-26 в 15:20, admin, рубрики: векторное произведение, кватернионы, октонионы, скалярное произведение

Чаще всего с векторным произведением мы знакомимся в курсе аналитической геометрии, где мы редко выходим в задачах за размерность три, поэтому может складываться впечатление, что векторное произведение обобщается на любую размерность, по аналогии со скалярным.

Вспомним, что такое векторное произведение векторов. Векторным произведением векторов и (обозначается ) называется вектор, перпендикулярный обоим векторам и и численно равный по длине площади параллелограмма, натянутого на соответствующие векторы, ту же длину выражает и определитель матрицы Грама векторов что влечёт следующее тождество:

Способы вычисления:

где - угол между векторами и .

$(a times b)=begin{pmatrix} i & j & k\ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{pmatrix}$ - а так мы можем узнать координаты вектора

Самое простое доказательство изложено в [1], его суть я изложу здесь. Основная идея состоит в построении универсального контрпримера для пространств большой размерности.

Для начала понадобятся некоторые свойства, векторного произведения. Их доказательства состоят в раскрывании скобочек и привидении подобных, так что это я опущу. Подробное доказательство изложено в [2].

Из первых четырёх свойств также следуют:

Введём несколько определений:

$S_0={u_0}, S_k=S_{k−1} cup {u_k} cup (S_{k−1} times u_k)$ , где $u_k perp S_{k-1}$
$S_i times S_j={u times v, text{ где } u in S_i text{ и } v in S_j}$

Утверждение 1

Оказывается, что при таком построении — ортонормированное множество. Более того, что $S_k times S_k=pm S_k text{ и } |S_k|=2^{k+1}−1$ .

Утверждение 2

Если и , то и .

Утверждение 3

Если и то .

Из утверждения 1 следует, что $n=2^{k+1} - 1$ , а из утверждений 2 и 3, что при нарушается тождество (). Дляи произведение просто равно 0. А вот, как строятся произведения в и :

Почему векторное произведение существует только в R^0, R^1, R^3, R^7? - 41

Почему векторное произведение существует только в R^0, R^1, R^3, R^7? - 43

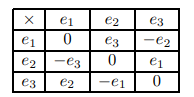
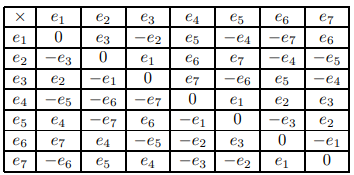
Векторное произведение в также можно описать с помощью кватернионов. В общем случае, если вектор представлен в виде кватерниона ${a_1}i + {a_2}j + {a_3}k,$ то векторное произведение двух векторов это кватернион, но после умножения надо отбросить действительную часть. Действительная часть будет равна отрицательному значению скалярного произведения двух векторов. Например:

Аналогично для семимерного пространства, только вместо кватернионов стоит использовать октонионы.

Список использованных источников:

Peter F. Mcloughlin, “When does a cross product on exists?”, Electronic copy found at: https://www.arxiv.org/pdf/1212.3515v6
Peter F. Mcloughlin, “Basic Properties of Cross Products”, Electronic copy found at: http://www.math.csusb.edu/faculty/pmclough/BP.pdf