В предыдущей статье я рассказывал, как можно реализовать алгоритм k-means на c# с обобщенной метрикой. В комментах можно почитать обсуждение того, насколько целесообразно использовать разные метрики, о математической природе использования разных метрик и тому прочее. Мне тогда хотелось привести красивый пример, но не было под рукой подходящих данных. И вот сегодня я столкнулся с задачей, которая хорошо иллюстрирует преимущества использования расстояния Махаланобиса в k-means кластеризации. Подробности под катом.
Обработка сырых данных
Итак у меня оказался некоторый массив 12-мерных данных, нужно было создать модель для прогнозирования тринадцатого бинарного поля, т.е. это задача классификации. Анализ как обычно начинается с того, что я загоняю весь массив без всякой предобработки в классификатор (я использую нейросети), и затем смотрю на результат, чтобы оценить масштабы бедствия. Редко это дает хороший результат, но позволяет понять вообще насколько все плохо. Я не был удивлен тем, что результат был не самый лучший, и я приступаю к следующему шагу анализа.
Визуализация
Визуализация позволяет наглядно оценить данные, например, можно увидеть, что данные образуют несколько групп, тогда возможно произвести кластеризацию, и обучить классификатор на каждый кластер. Получается простая двухступенчатая гибридная модель, по результату кластеризации строится первый классификатор на несколько классов (кластеров, которые обнаружены алгоритмом кластеризации), а затем для каждого класса/кластера используется свой классификатор для целевого поля. Как мы знаем, алгоритм k-means на вход принимает количество кластеров и разбивает данные на указанное число групп. Вместо того, чтобы перебирать количество кластеров и искать разбиение с наименьшей стоимостью, можно визуализировать данные и увидеть эти группы. Но есть и другая проблема, например, разбив данные по расстоянию Евклида, мы можем получить очень неявные границы кластеров, они будут очень близко друг к другу, и тем самым точность системы в целом уменьшается.
Итак, я приступаю к визуализации, но, правда, визуализаировать 12-мерное пространство не очень просто, так что мне нужно уменьшить размерность до 3 или 2. Я для начала выбираю два, т.к. это проще. Для уменьшения размерности я использую метод главных компонент, кстати ту самую реализацию, описанную в позапрошлой статье.
В итоге я получил такую картинку:
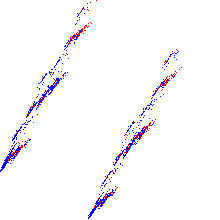
Синие и красные точки — это как раз два класса, образованные целевым полем.
Кластеризация
По картинке выше видно, что проекция данных образует явные две группы с очень четкой границей. Теперь нужно сделать кластеризацию k-means с параметром 2. Но вот в чем вопрос, какую метрику использовать для этого. Евклидова метрика строит круглые гауссианы (почему именно гауссианы, можно прочитать мой коммент к предыдущей статье), но даже невооруженным глазом видно, что если описать окружности вокруг кластеров, то они будут пересекаться.
Вот как выглядит кластеризация с Евклидовой метрикой:

Граница очень нечеткая, да и вообще кластеры получились совсем не те, что хотелось.
Кластеризация с расстоянием Махаланобиса строит эллипсообразные гауссианы, и для первой картинки очень легко мысленно нарисовать два непересекающихся эллипса, описанные вокруг кластеров.
Вот результат такой кластеризации:

Профит
Пока не ясно профит или нет, но кластеризация дала мне две четкие группы данных, и теперь можно строить первую ступень модели. Или работать с каждым из кластеров, как с отдельной задачей. Далее, для каждой группы будет обучен классификатор по целевому полю, ну и так далее, но это уже не в рамках этой статьи -)
Автор: mephistopheies

