Разработка класса для работы с цепями Маркова

Сегодня я хотел бы поведать вам о написании класса для упрощения работы с цепями Маркова.

Прошу под кат.

Начальные знания:

Представление графов в форме матрицы смежности, знание основных понятий о графах. Знание C++ для практической части.

Теория

Це́пь Ма́ркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего).

Если говорить простыми словами, то Цепь Маркова — это взвешенный граф. В его вершинах находятся события, а в качестве веса ребра, соединяющего вершины A и B — вероятность того, что после события A последует событие B.

О применении цепей Маркова написано довольно много статей, мы же продолжим разработку класса.

Приведу пример цепи Маркова:

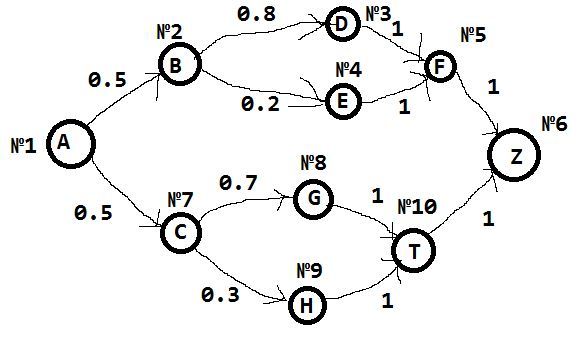
В дальнейшем мы будем рассматривать в качестве примера эту схему.

Очевидно, что если из вершины A есть только одно исходящее ребро, то его вес будет равен 1.

Обозначения

В вершинах у нас находятся события (от A, B, C, D, E...). На ребрах вероятность того, что после i-го события будет событие j > i. Для условности и удобства я пронумеровал вершины (№1, №2 и т.д ).

Матрицей будем называть матрицу смежности ориентированного взвешенного графа, которым изображаем цепь Маркова. ( об этом далее ). В данном частном случае эта матрица называется также матрицей переходных вероятностей или просто матрицей перехода.

Матричное представление цепи Маркова

Представлять цепи Маркова мы будем при помощи матрицы, именно той матрицы смежности, которой представляем графы.

Напомню:

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.

Подробнее о матрицах смежности — в курс дискретной математики.

В нашем случае матрица будет иметь размер 10x10, напишем ее:

0 50 0 0 0 0 50 0 0 0
0 0 80 20 0 0 0 0 0 0
0 0 0 0 100 0 0 0 0 0
0 0 0 0 100 0 0 0 0 0
0 0 0 0 0 100 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 70 30 0
0 0 0 0 0 0 0 0 0 100
0 0 0 0 0 0 0 0 0 100
0 0 0 0 0 100 0 0 0 0


Идея

Посмотрите внимательнее на нашу матрицу. В каждой строке у нас есть ненулевые значения в тех столбцах, чей номер совпадает с последующим событием, а само ненулевое значение — вероятность, что это событие наступит.

Таким образом, мы имеем значения вероятности наступления события с номером, равным номеру столбца после события с номером, равным строки.

Те кто знают теорию вероятностей могли догадаться, что каждая строка — это функция распределения вероятностей.

Алгоритм обхода цепи Маркова

1) инициализируем начальную позицию k нулевой вершиной.
2) Если вершина не конечная, то генерируем число m от 0...n-1 на основе распределения вероятности в строке k матрицы, где n — число вершин, а m — номер следующего события (!). Иначе выходим
3) Номер текующей позиции k приравниваем к номеру сгенерированной вершине
4) На шаг 2

Замечание: вершина конечная если распределение вероятностей нулевое (см. 6-ю строку в матрице).

Довольно изящный алгоритм, так ведь?

Реализация

В эту статью я хочу отдельно вынести код реализации описанного обхода. Инициализация и заполнение цепи Маркова не несут особого интереса (полный код см. в конце).

template <class Element> Element *Markov<Element>::Next(int StartElement = -1)
{

	if (Markov<Element>::Initiated) // если матрица смежности создана
	{

		if (StartElement == -1) // если стартовый элемент по умолчанию
			StartElement = Markov<Element>::Current; // то продолжаем ( в конструкторе Current = 0 )

		std::random_device              rd;
		std::mt19937                    gen(rd());
		std::discrete_distribution<>    dicr_distr(Markov<Element>::AdjacencyMatrix.at(Current).begin(),
			Markov<Element>::AdjacencyMatrix.at(Current).end()); // инициализируем контейнер для генерации числа на основе распределения вероятности


		int next = dicr_distr(gen); // генерируем следующую вершину
		if (next == Markov<Element>::size()) // тонкости работы генератора, если распределение вероятностей нулевое, то он возвращает количество элементов 
			return NULL;

		Markov<Element>::Current = next; // меняем текущую вершину
		return &(Markov<Element>::elems.at(next)); // возвращаем значение в вершине
	}
	return NULL;
}

Данный алгоритм выглядит особенно просто благодаря особенностям контейнера discrete_distribution. На словах описать, как работает этот контейнер довольно сложно, поэтому возьмем в пример 0-ю строку нашей матрицы:

0 50 0 0 0 0 50 0 0 0

В результате работы генератора он вернет либо 1, либо 6 с вероятностями в 0.5 для каждой. То есть возвращает номер столбца ( что эквивалентно номеру вершины в цепи ) куда следует продолжить движение дальше.

Пример программы, которая использует класс:

#include <iostream>
#include "Markov.h"
#include <string>
#include <fstream>

using namespace std;

int main()
{
	Markov<string> chain;
	ofstream outs;
	outs.open("out.txt");
	ifstream ins;
	ins.open("matrix.txt");

	int num;
	double Prob = 0;
	(ins >> num).get(); // количество вершин
	string str;
	for (int i = 0; i < num; i++)
	{
		getline(ins, str);
		chain.AddElement(str); // добавляем вершину
	}
	if (chain.InitAdjacency()) // инициализируем матрицу нулями
	{
		for (int i = 0; i < chain.size(); i++)
		{
			for (int j = 0; j < chain.size(); j++)
			{
				(ins >> Prob).get();
				if (!chain.PushAdjacency(i, j, Prob)) // вводим матрицу
				{
					cerr << "Adjacency matrix write error" << endl;
				}
			}
		}

		outs << chain.At(0) << " "; // выводим 0-ю вершину
		for (int i = 0; i < 20 * chain.size() - 1; i++) // генерируем 20 цепочек
		{
			string *str = chain.Next();
			if (str != NULL) // если предыдущая не конечная
				outs << (*str).c_str() << " ";  // выводим значение вершины
			else
			{
				outs << std::endl; // если конечная, то начинаем с начала
				chain.Current = 0;
				outs << chain.At(0) << " ";

			}
		}

		chain.UninitAdjacency(); // понятно
	}
	else
		cerr << "Can not initialize Adjacency matrix" << endl;;

	ins.close();
	outs.close();
	cin.get();
	return 0;
}

Пример вывода, который генерирует программа:

Мы видим, что алгоритм работает вполне сносно. В качестве значений можем указывать что угодно.

Из иллюстрации цепи Маркова видно, что A B D F Z наиболее вероятная последовательность событий. Она же чаще всего и проявляется. Событие E встречается реже всего

Конфигурационный файл, использовавшийся в примере:

Заключение

Таким образом мы видим, что к цепям Маркова применимы алгоритмы на графах и выглядят эти алгоритмы довольно красиво. Если кто-то знает более лучшую реализацию, то прошу отписываться в комментариях.

Полный код и readme на гитхабе: код

Всем спасибо за внимание.

Автор: SolidMinus

Источник